
西安在子科枝大拳 电子工学院DD School of Electronic Engineering,Xidian University http://see.xidian.edu-cn 场论与复变函数 主井:关】 2011年8月31日星期三

Review 场论导论 矢量场的矢量线 单值、连续且具 数量场的等值面与等值线 有—阶连续偏导 数量场的方向导数与梯度 。矢量场的通量与散度 。矢量场的环量与旋度 IN.EDU.CN lexu@mail.xidian.edu.cn
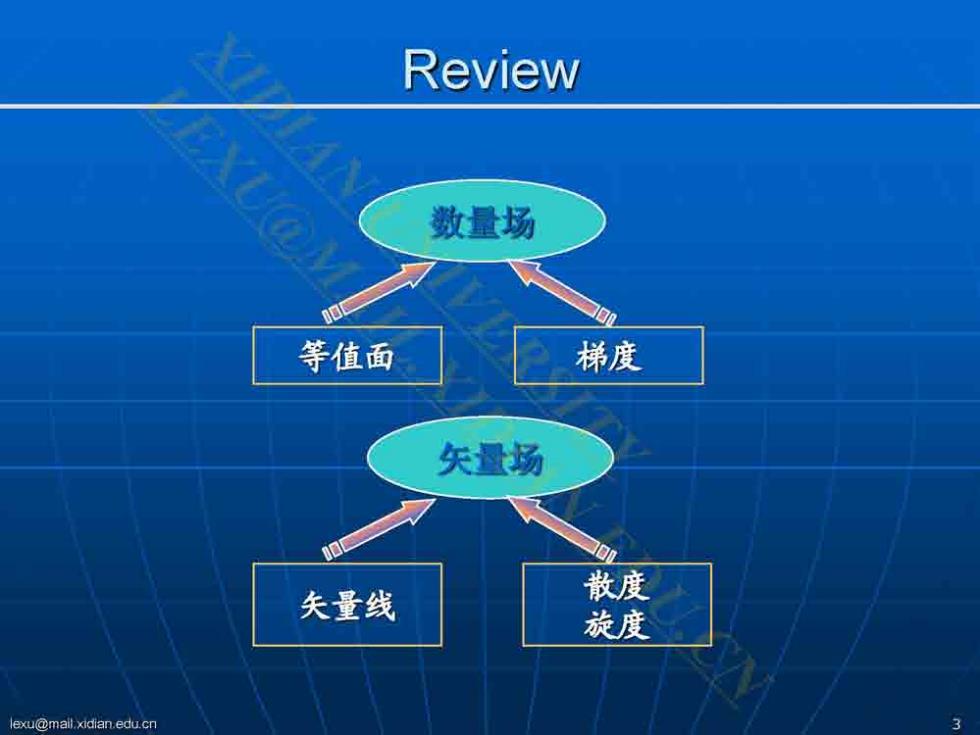
Review EXU@M 数量场 等值面 梯度 矢量场 夫量线 散度 旋度 lexu@mall.xidian.edu.cn

Review 通量 ·设AM0为一矢量场,沿其中有向曲面S正(负) 侧曲面积分称为矢量场AM)向S正(负)侧穿过 曲面S的通量。 如果曲面是一个开曲面,则 w-1A-d5-1 A.nds 。如果曲面是一个闭曲面,则 w=8 A.ds lexu@mail.xidian.edu.cn
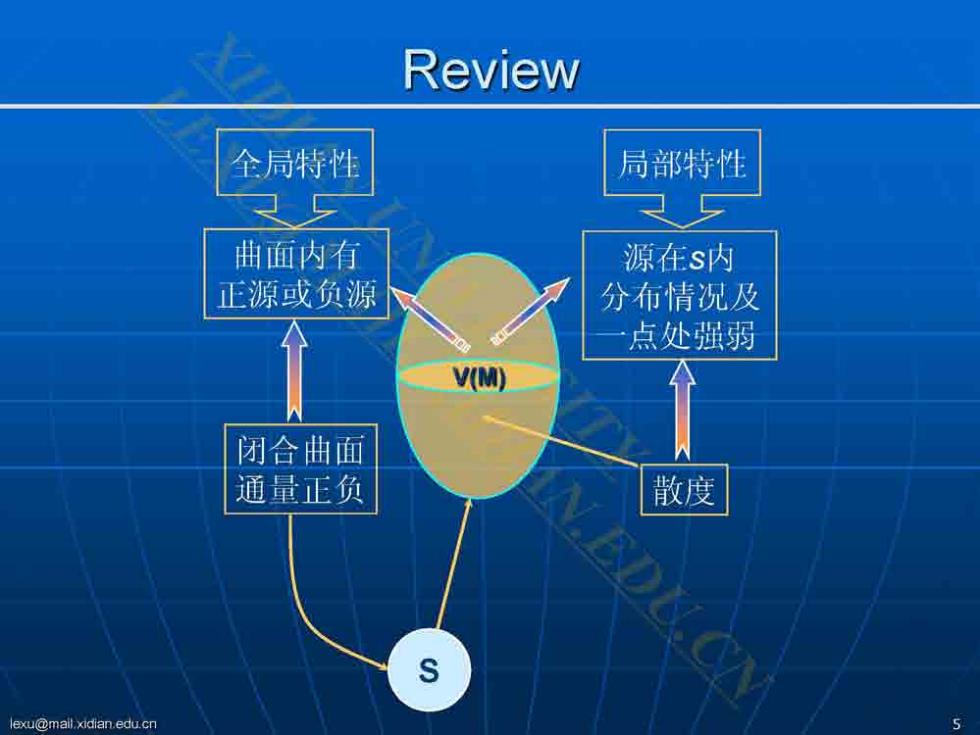
Review 全局特性 局部特性 曲面内有 源在s内 正源或负源 分布情况及 点处强弱 V(M) 闭合曲面 通量正负 N.EDU.CN 散度 lexu@mall.xidian.edu.cn

Review 散度: ·设M是矢量场中的一点,在M的某个邻域内取 包含M在内的任一闭合曲面,其所包含区域 的体积为△V,以△φ表示穿出△s的通量。若 当该区域以任意方式缩向点M时, A西 △V 极限存在,则称之为矢量场在点M处的散度。 记为 月A: div 4=lim △0 lim △@→M△V AQ今AM △ lexu@mail.xidian.edu.cn

Review ·环量 。定义:设有矢量场, 则沿场中某一封闭的有向曲线的 曲线积分工五称为此矢量场按积分所取 方向沿曲线的环量。(其中d=无dL) 。直角坐标系A=A(x,y)+Ax,2)0+A(c,y,)2 i=dl cosa¥dl cos B v+dl cosy2生dx+dy+db2 Γ=AdI=∮A+A+A,d正 lexu@mall.xidian.edu.cn
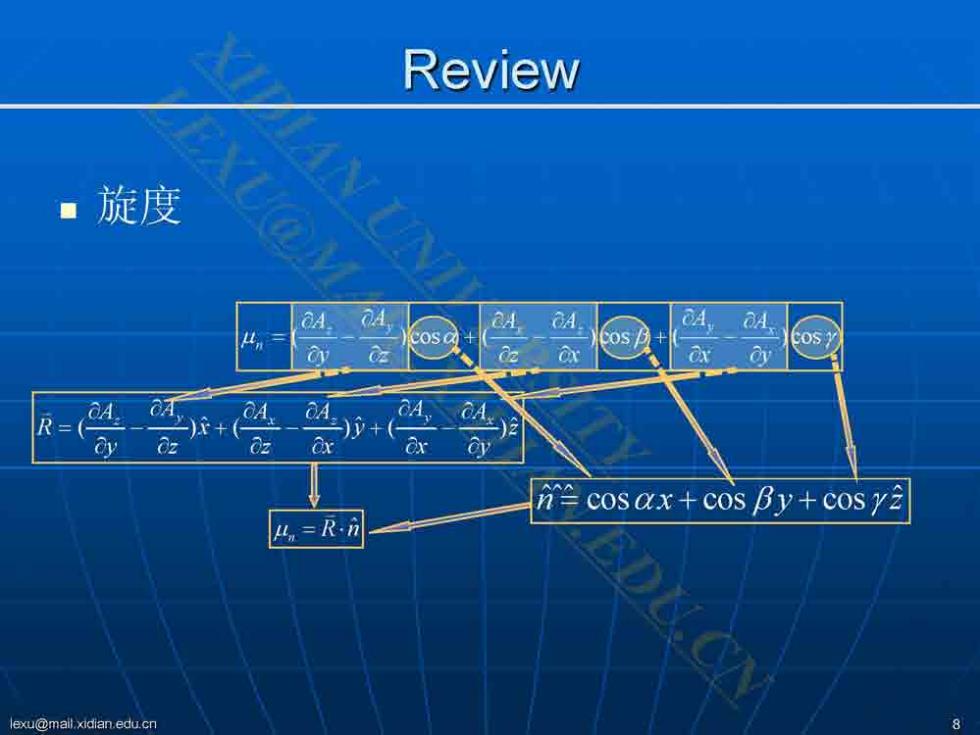
Review 旋度 os+ ncos ax+cos By+cos y2 凸=R7 EDU.CN lexu@mail.xidian.edu.cn

Review 回顾可算子: ·直角坐标系定义:0+ 0+ 02 ·梯度: g7atdw=Vi月 V+ 矢量 ax oy dz 散度: 函=.A @4+4+4 标量 。旋度: o1A=7×A A 0可4 28aA 矢量 lexu@mall.xidian.edu.cn

第4讲特殊矢量场 有势场 管形场 调和场 lexu@mail.xidian.edu.cn 10