
西安电子科枝大学 电子工程学院《D School of Electronic Engineering.Xidian University http:/ xidian.edu.cn n.edu.ch 场论与复变函数 xuamail.x 主讲:徐乐 2011年11月6日星期日
lexu@mail.xidian.edu.cn

Review lexuamail.xidian.edu.cx ■矢量代数 矢性函数 ■矢性函数微积分 ler@mailridianedu.cn
lexu@mail.xidian.edu.cn
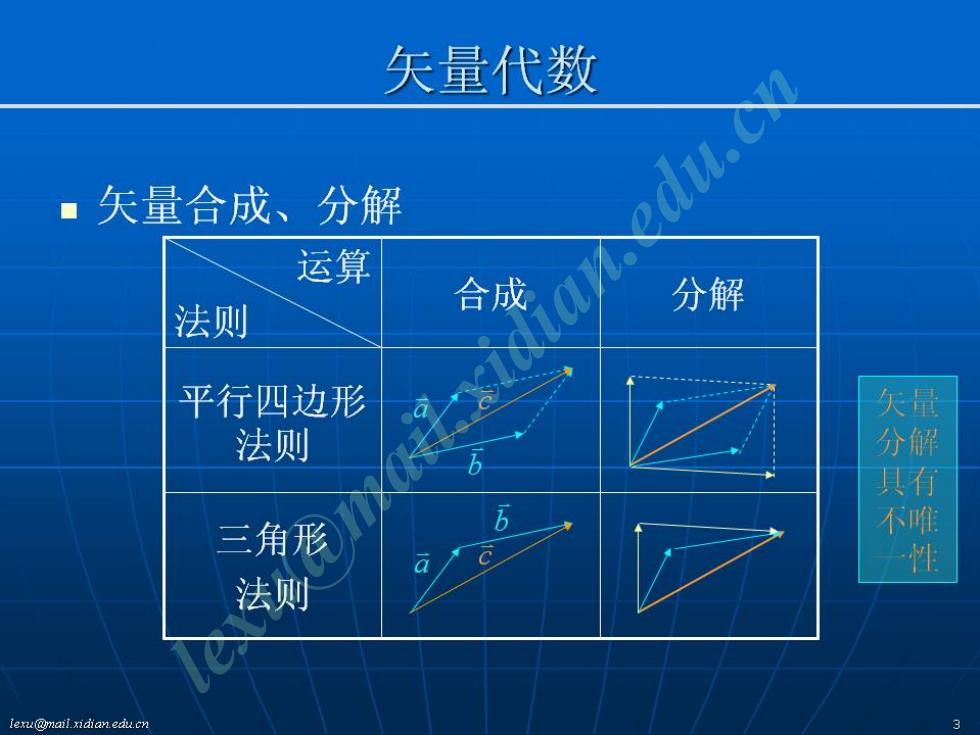
矢量代数 ■矢量合成、分解 edu.Cx 运算 分解 法则 平行四边形 天量 法则 分解 具有 三角形 b 不唯 a 性 法则 lexu@mail xidianedu.cn
lexu@mail.xidian.edu.cn

矢性函数微积分 矢性函数 A=A()元+A,()+A(0) edu. 运算 LA]=LA(t)R+耳4(+LA,()]脸 L是算子符号,代表一种运算(极限、导数、积分) 些基本矢量运算 a.b=a.b.cos0 戈习 2 axb= a a a(bxc)=c(axb)=b·(c×a) ax(b×c)=(a·c)b-(a-b)g iexu@mail xidian edu.cn
lexu@mail.xidian.edu.cn

矢性函数 ■矢性函数 。矢端曲线: ◆ 将空间中所有矢量的起点 dian.edu.ox 固定在坐标原点,当变 时,矢量的终点描绘出 条曲线1,该曲线称为矢性 函数的矢端曲线或图形。 认为所有大小相等、方向 相同的矢量是同一个矢量 ◆ 矢性函数的表示式也称为 曲线的矢量方程: A日A,(0+A,0P+A() lexu@mail xidianedu.cn
lexu@mail.xidian.edu.cn

第2讲数量场 场论导论 矢量场的矢量线 an.edu.cn 数量场的等值面与等值线 lexu@mail. 数量场的方向导数与梯度 lexu@mail.xidian.edu.cn 6
lexu@mail.xidian.edu.cn

场论导论 场论初窥 ·如果在某一空间区域内的每一点,都对应着某个物理 量的一个确定的值,则称在此区域内确定了该物理量 的一个场。换句话说,在某空间区域中,物理量的 无穷集合表示一种场。 ■在研究物理系统中温度、压力、密度等在一定空间的分布状 态时,数学上只需用一个代数变量来描述,这些代数变量(即 标量函数)所确定的场称为数量场,如温度场Tx,y2)电位场 c,y2)等。 ■ 而在许多物理系统中,其状态不仅需要确定其大小,同时还 需确定它们的仿向,这就需要用一个矢量来描述,因此称为 矢量场,例如电场、磁场、流速场等等。 lexu(@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
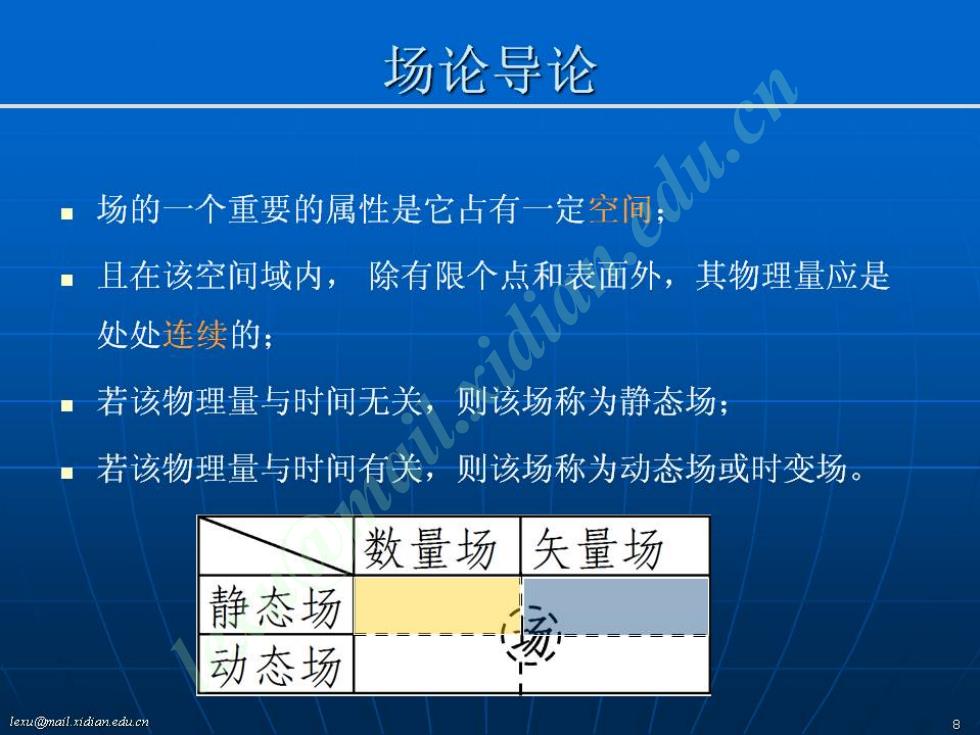
场论导论 场的一个重要的属性是它占有一定空间: ■且在该空间域内,除有限个点和表面外,其物理量应是 处处连续的: 若该物理量与时间无关, 则该场称为静态场: ■若该物理量与时间有关,则该场称为动态场或时变场。 数量场矢量场 静态场 动态场 leru(@mail xidian.edu.cn
lexu@mail.xidian.edu.cn

矢量场的矢量线 矢量场 A=AM) edu. ·为矢量场中的任意一点 ·矢量场中分布在各点处的矢量是场点的函数 。直角坐标系下,矢量场可表示为: PxCOAY 单值、连续且具 +A,(x,2)月 有一阶连续偏导 +A(x,yz)泥
lexu@mail.xidian.edu.cn

矢量场的矢量线 。矢量线 edu. ·曲线在其上每一点处都与该 点的矢量A相切: 。 矢量线方程: d dz A ·Note:A不为0,且其3个分 量单值、连续且具有一阶连 续偏导数时,矢量线存在且 互不相交; 矢量面:通过曲线C的矢量 线构成的曲面 。 矢量管:曲线C封闭时的矢 量面。 leru(@mail xidian.edu.cn
lexu@mail.xidian.edu.cn