
第8章在电工电子中的应用
第8章 在电工电子中的应用
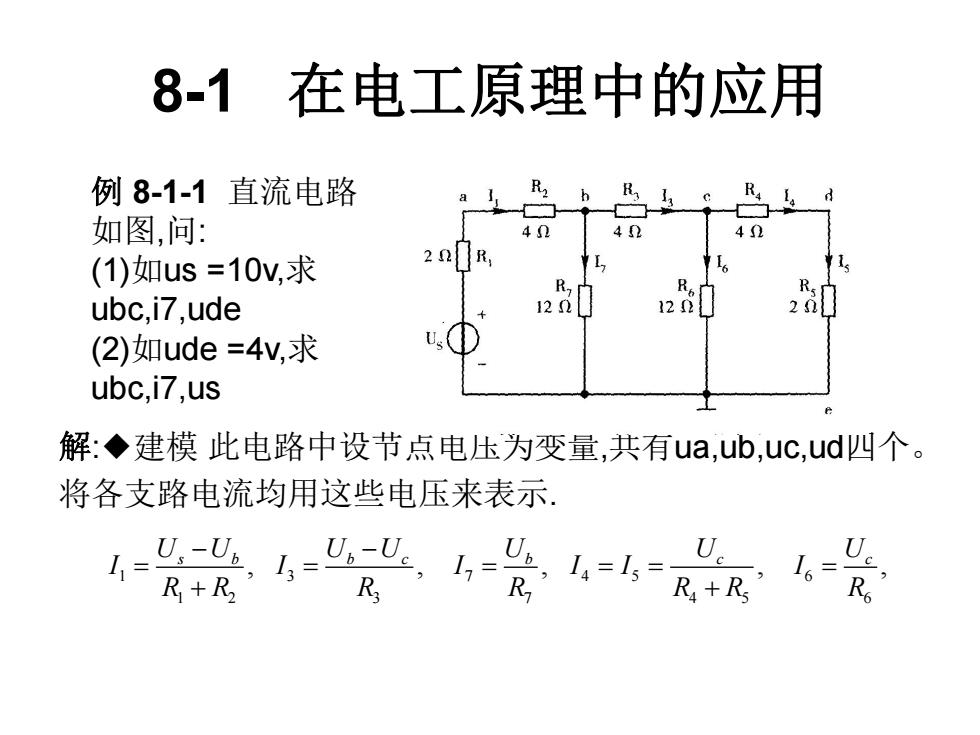
8-1 在电工原理中的应用 例8-1-1直流电路 R 如图,问: 42 42 (1)如us=10V,求 22R ubc,i7,ude 12 122 (2)如ude=4v,求 ubc,i7,us 解:◆建模此电路中设节点电压为变量,共有ua,ub,uc,ud四个。 将各支路电流均用这些电压来表示. R+R R R R
8-1 在电工原理中的应用 解:◆建模 此电路中设节点电压为变量,共有ua,ub,uc,ud四个。 将各支路电流均用这些电压来表示. 例 8-1-1 直流电路 如图,问: (1)如us =10v,求 ubc,i7,ude (2)如ude =4v,求 ubc,i7,us 1 3 7 4 5 6 1 2 3 7 4 5 6 , , , , , Us Ub Ub Uc Ub Uc Uc I I I I I I R R R R R R R

方程的建立 对b点和c点列出节点电流方程:I1=3+7,3=4+6,将上述 各值代入化简,得 () (2) 对问题(1)给出Us时,这两个方程中只有两个未知数Ub和 Uc,可以写成矩阵方程 -。 U;
方程的建立 对b点和c点列出节点电流方程:I1=I3+I7,I3=I4+I6,将上述 各值代入化简,得 对问题(1)给出Us时,这两个方程中只有两个未知数Ub和 Uc,可以写成矩阵方程 3 1 2 7 3 1 2 3 3 4 5 6 1 1 1 1 (1) 1 1 1 1 0 (2) s b c b c U U U R R R R R R R U U R R R R R 11 12 13 1 2 21 22 23 0 s b b s c c U U a a U a R R U U a a U a A1

编程方法及运行结果 读者可从方程(1),(2)中找到a11,a12,a21,a22及 a13,a23的表达式,并用矩阵左除解出Ub和Uc。 再由 R一U,1,=R e=U,-U。U=R十R} _U6 即可得到问题(1)的解。 对问(2),可以推出类似的矩阵表达式,只是输入输出量 不同,请读者自行推导,并与下面的程序exn811对照。 由于同一系统的特征矩阵有许多相同的项,编程时可以利用这 个特点来简化赋值过程 ◆运行程序exn811的结果为 输入us=10时,ubc=2.2222,ude=0.7407,i7=0.3704 输入ude=4时,ubc=12.0000,i7=2.0000,us=54.0000
编程方法及运行结果 • 读者可从方程(1),(2)中找到a11,a12,a21,a22及 a13,a23的表达式,并用矩阵左除解出Ub和Uc。 再由 即可得到问题(1)的解。 对问(2),可以推出类似的矩阵表达式,只是输入输出量 不同,请读者自行推导,并与下面的程序exn811对照。 由于同一系统的特征矩阵有许多相同的项,编程时可以利用这 个特点来简化赋值过程 ◆运行程序exn811的结果为 输入us=10 时, ubc = 2.2222, ude = 0.7407, i7 = 0.3704 输入ude=4 时, ubc = 12.0000, i7 = 2.0000, us = 54.0000 5 7 4 5 7 , , , b bc b c de c R U U U U U U I R R R

程序exn811 r1=2;r2=4;r3=4;r4=4;r5=2;r6=12;r7=12;%为元件赋值 %将各系数矩阵赋值 a11=1/(r1+r2)+1/r3+1/r7;a12=-1/r3;a13=1/(r1+r2); a21=1/r3,a22=-1/r3-1/(r4+r5)-1/r6;a23=0; us=input('us='); %输入解(1)的己知条件 A1=[a11,a12;a21,a22] %列出系数矩阵A1 u=A1N[a13*us;0] u=[ub;uc] ubc=u(1)-u(2),ude=u(2)*r5/(r4+r5),i=u(1)/r7 %解(1) ude=input('ude=), %输入解(2)的已知条件 A2=[A1,[a13;a23];0,r5/r4+r5),0]%列出系数矩阵A2 u=A20;0;ude], %u=[ub;uc;us] ubc=u(1)-u(2),i=u(1)/r7, uS=(r1+r2)*(u(1)*a11+u(2)*a12) %解(2)
程序exn811 r1=2;r2=4;r3=4;r4=4;r5=2;r6=12;r7=12; %为元件赋值 %将各系数矩阵赋值 a11=1/(r1+r2)+1/r3+1/r7;a12=-1/r3;a13=1/(r1+r2); a21=1/r3;a22=-1/r3-1/(r4+r5)-1/r6; a23=0; us=input('us='); % 输入解(1)的已知条件 A1=[a11,a12;a21,a22] % 列出系数矩阵A1 u=A1\[a13*us;0] % u=[ub;uc] ubc=u(1)-u(2),ude=u(2)*r5/(r4+r5),i=u(1)/r7 % 解(1) ude=input('ude='), % 输入解(2)的已知条件 A2=[A1,[a13;a23];0,r5/(r4+r5),0] % 列出系数矩阵A2 u=A2\[0;0;ude], %u=[ub;uc;us] ubc=u(1)-u(2),i=u(1)/r7, us=(r1+r2)*(u(1)*a11+u(2)*a12) % 解(2)
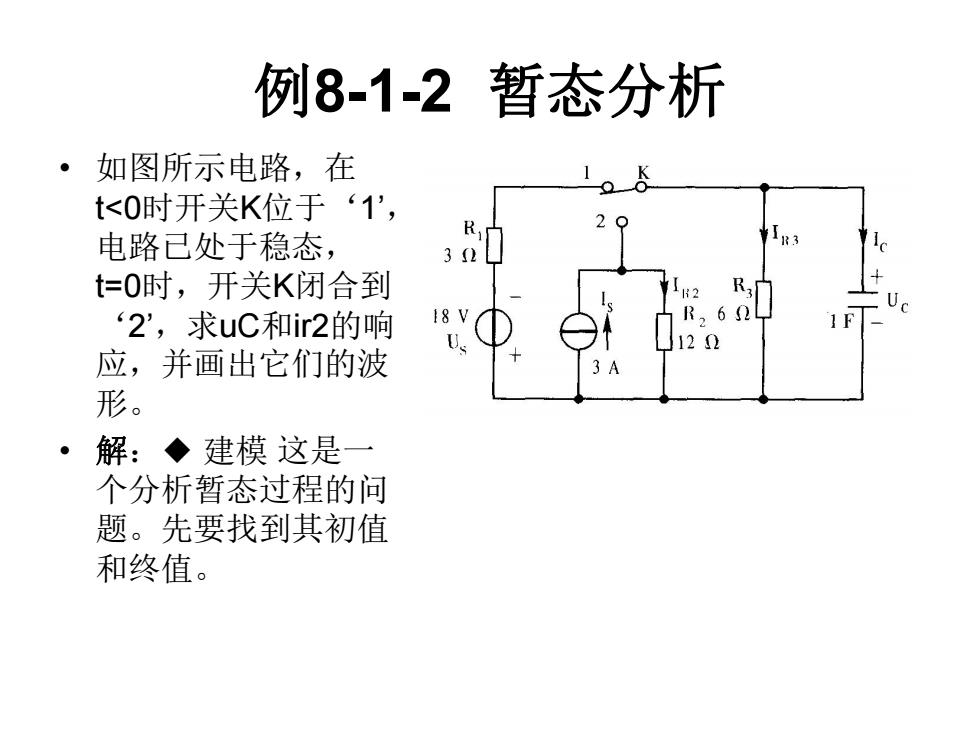
例8-1-2暂态分析 。1 如图所示电路,在 t<0时开关K位于‘1', 电路已处于稳态, 3(2 t=0时,开关K闭合到 2',求uC和ir2的响 18 V 应,并画出它们的波 形。 ·解:◆建模这是 个分析暂态过程的问 题。先要找到其初值 和终值
例8-1-2 暂态分析 • 如图所示电路,在 t<0时开关K位于‘1’ , 电路已处于稳态, t=0时,开关K闭合到 ‘2’ ,求uC和ir2的响 应,并画出它们的波 形。 • 解:◆ 建模 这是一 个分析暂态过程的问 题。先要找到其初值 和终值

初值的分析 ·在t=0时uc(0-)=-12v,ic(0-)=0,由于R2是电流源 s的唯一外部通路,故IR2(0-)=s=3;当t=0+时, 因为电容器端电压不可能突变,仍有uc(0+)=uc(0 )=-12V,电流源向两个电阻和一个电容的并联系统 供电,两个电阻的电流应等于电容电压除以电阻, 即 ● 1e0,)-0)-14,1a0,)=0)-21 ● R R 而电容的充电电流为电流源电流减去电阻电流,故 ic(0+)=is-ir2(0+)-ir3(0+)=3-(-1)-(-2)=6A
初值的分析 • 在t=0时 uc(0-)=-12v, ic(0-)=0 ,由于R2是电流源 Is的唯一外部通路,故IR2(0-)=Is=3;当t=0+时, 因为电容器端电压不可能突变,仍有uc(0+)= uc(0- )=-12v,电流源向两个电阻和一个电容的并联系统 供电,两个电阻的电流应等于电容电压除以电阻, 即 • • • 而电容的充电电流为电流源电流减去电阻电流,故 • ic(0+)=is- ir2(0+)- ir3(0+)= 3-(-1)-(-2)=6A 2 3 2 3 (0 ) (0 ) (0 ) 1 , (0 ) 2 c c R R U U I A I A R R

终值的分析 再分析终值,达到稳态后,电容中将无电流,电 流源的全部电流将在两个电阻之间分配,保证其 端电压相同(也就是电容上的终电压)。结果应为 ucf=12v,ir2f=1A. ·初值和终值之间的过渡波形u(代)按三要素计算。所 谓三要素是指初值u0、终值uf和该段的充放电时 常数T,表示式为: 40=4,+(46-4,))et-6/ 用MATLAB语句可写成:u=uf+(u0-uf*eXp(-(t-tO)T) 在求多段波形时,每段的初始时刻t0可能不同, 需要予以注意
终值的分析 • 再分析终值,达到稳态后,电容中将无电流,电 流源的全部电流将在两个电阻之间分配,保证其 端电压相同(也就是电容上的终电压)。结果应为 ucf=12v,ir2f=1A. • 初值和终值之间的过渡波形u(t)按三要素计算。所 谓三要素是指初值u0、终值uf和该段的充放电时 常数T,表示式为: 用MATLAB语句可写成:u=uf+(u0-uf)*exp(-(t-t0)/T). 在求多段波形时,每段的初始时刻t0可能不同, 需要予以注意。 0 / 0 ( ) t t T f f u t u u u e

程序exn812 r1=3;uS=18;is=3;r2=12;r3=6;C=1;%给出原始数据 uc0=-12;ir20=uc0/r2;ir30=uc0/r3;%算出初值 ic0=is-ir20-ir30; ir2f=is*r3/(r2+r3); %算出终值 ir3f=is*r2/(r2+r3); ucf=ir2f*r2;icf=0; t=[-2:0]-eps:0-eps,0:15];c %注意在t=0附近设两个点 uc(1:3)=-12;ir2(1:3)=3; %t←0时的值 T=r2*r3/(r2+r3)*C; %求充电时常数 uc(4:19)=ucf+(uc0-ucf0*exp(-t(4:19)/T);% ir2(4:19)=ir2f+(ir20-ir2)*exp(-t(4:19)/T);%三要素法求输出
程序exn812 r1=3;us=18;is=3;r2=12;r3=6;C=1; % 给出原始数据 uc0=-12;ir20=uc0/r2;ir30=uc0/r3; % 算出初值 ic0=is-ir20-ir30; ir2f=is*r3/(r2+r3); % 算出终值 ir3f=is*r2/(r2+r3); ucf=ir2f*r2; icf=0; t=[[-2:0]-eps:0-eps,0:15]; % 注意在t=0附近设两个点 uc(1:3)=-12;ir2(1:3)=3; % t<0时的值 T = r2*r3/(r2+r3)*C; % 求充电时常数 uc(4:19)=ucf+(uc0-ucf)*exp(-t(4:19)/T); % ir2(4:19)=ir2f+(ir20-ir2f)*exp(-t(4:19)/T); % 三要素法求输出
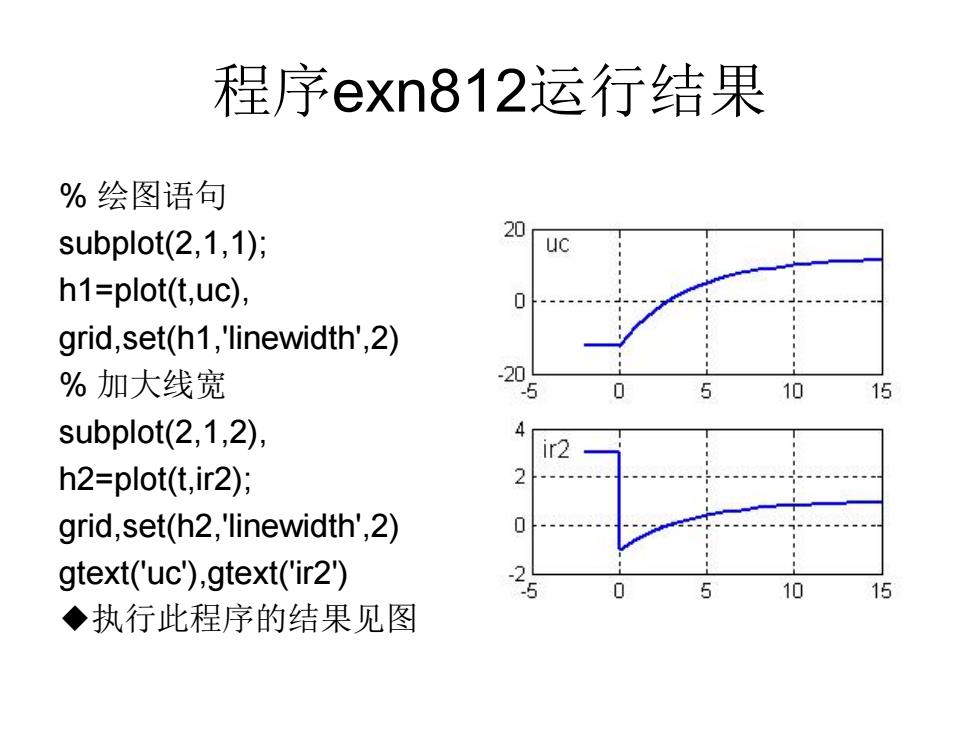
程序eXn812运行结果 %绘图语句 subplot(2,1,1); 20 h1=plot(t,uc), 0 grid,set(h1,'linewidth',2) %加大线宽 20 -5 0 subplot(2,1,2). h2=plot(t,ir2); grid,set(h2,'linewidth',2) gtext('uc),gtext('ir2) 10 ◆执行此程序的结果见图
程序exn812运行结果 % 绘图语句 subplot(2,1,1); h1=plot(t,uc), grid,set(h1, 'linewidth' ,2) % 加大线宽 subplot(2,1,2), h2=plot(t,ir2); grid,set(h2, 'linewidth' ,2) gtext('uc'),gtext('ir2') ◆执行此程序的结果见图