西安电子科技大学：《MATLAB及其在电子信息课程中的应用》课程PPT教学课件（讲稿）第五章 在电路中的应用

例5.1电阻电路的计算 用基尔霍夫定理列方程组 (R+R2+R3)i2-R4=4购 -Ra+(R+R+R)i-Rsi。=0 -Ri+(R+R+R7)i。=0 把方程组写成矩阵形式为 图5.1例5.1的电路图 R+R2+R3 -R3 0 1 -R3 R+4+R -Rs 0 0 -R5 Rs+R6+Ric 0

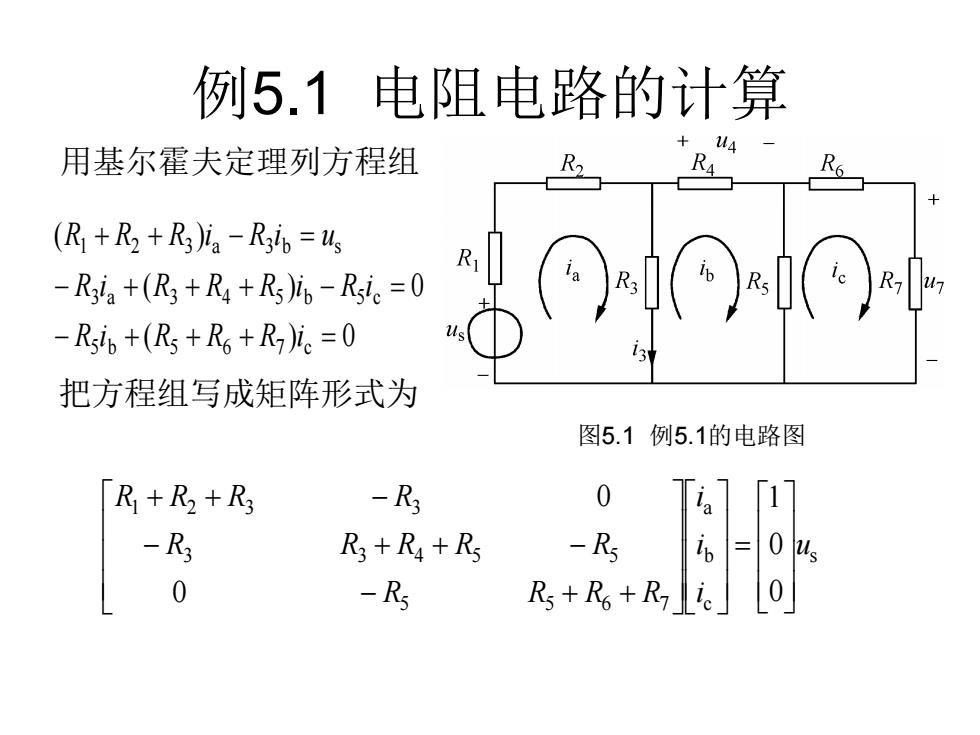
例5.1 电阻电路的计算 把方程组写成矩阵形式为 图5.1 例5.1的电路图 ( ) 0 ( ) 0 ( ) 5 b 5 6 7 c 3 a 3 4 5 b 5 c 1 2 3 a 3 b s − + + + = − + + + − = + + − = R i R R R i R i R R R i R i R R R i R i u s c b a 5 5 6 7 3 3 4 5 5 1 2 3 3 0 0 1 0 0 u i i i R R R R R R R R R R R R R           =                     − + + − + + − + + − 用基尔霍夫定理列方程组

例5.2含受控源的电阻电路 R R2 1 1 +1 西 4=-ki+R R R 6R R ·写成矩阵形式有 ·图5.2例5.2的电路图

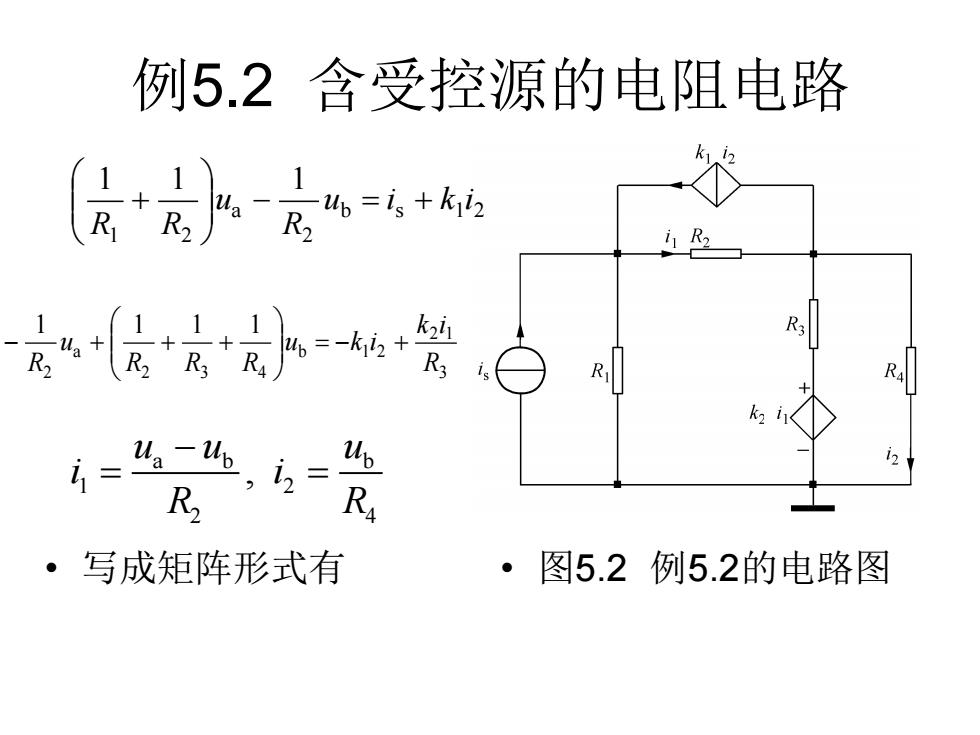
例5.2 含受控源的电阻电路 • 图5.2 例5.2的电路图 b s 1 2 2 a 1 2 1 1 1 u i k i R u R R − = +         + 3 2 1 b 1 2 2 3 4 a 2 1 1 1 1 R k i u k i R R R u R = − +         − + + + a b b 1 2 2 4 , u u u i i R R − = = • 写成矩阵形式有

续例5.2含受控源的电阻电路 1 1 1 0 -k1 1W8 1 R R2 R2 1 1 +1+1 2 up 0 R R2 R3 R R3 1 s -1 0 R2 R2 i 0 1 0 0

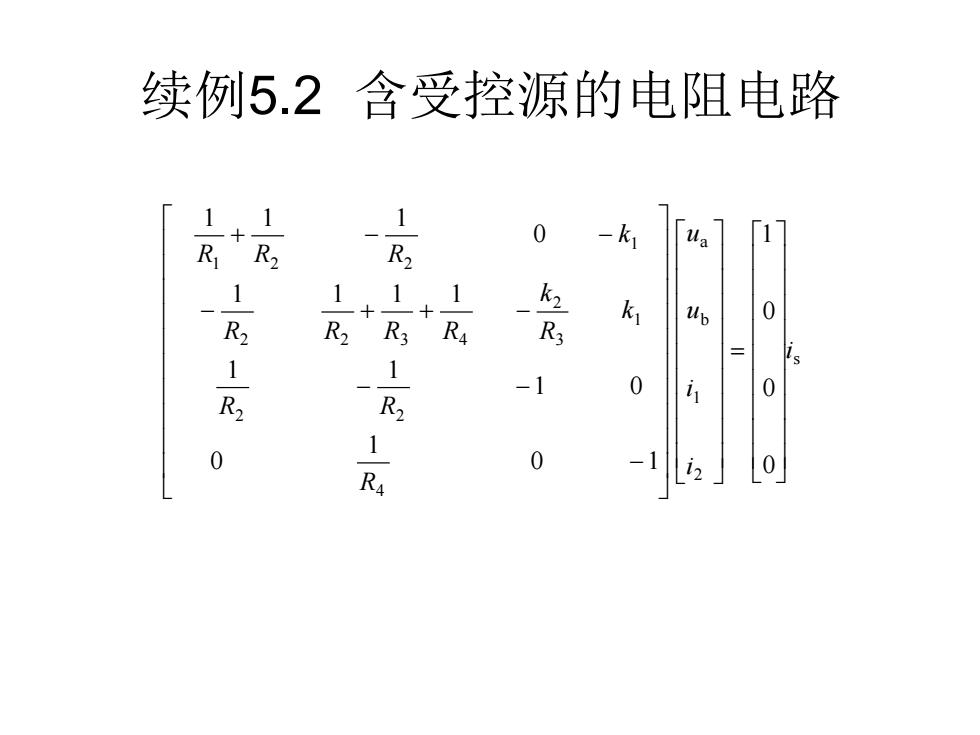
续例5.2 含受控源的电阻电路 s 2 1 b a 4 2 2 1 3 2 2 2 3 4 1 1 2 2 0 0 0 1 0 1 1 0 1 0 1 1 1 1 1 1 0 1 1 1 i i i u u R R R k R k R R R R k R R R                       =                                               − − − − + + − + − −

例5.3戴维南定理 R R3 241 2R ua a R2 R2 0 (a) (b)

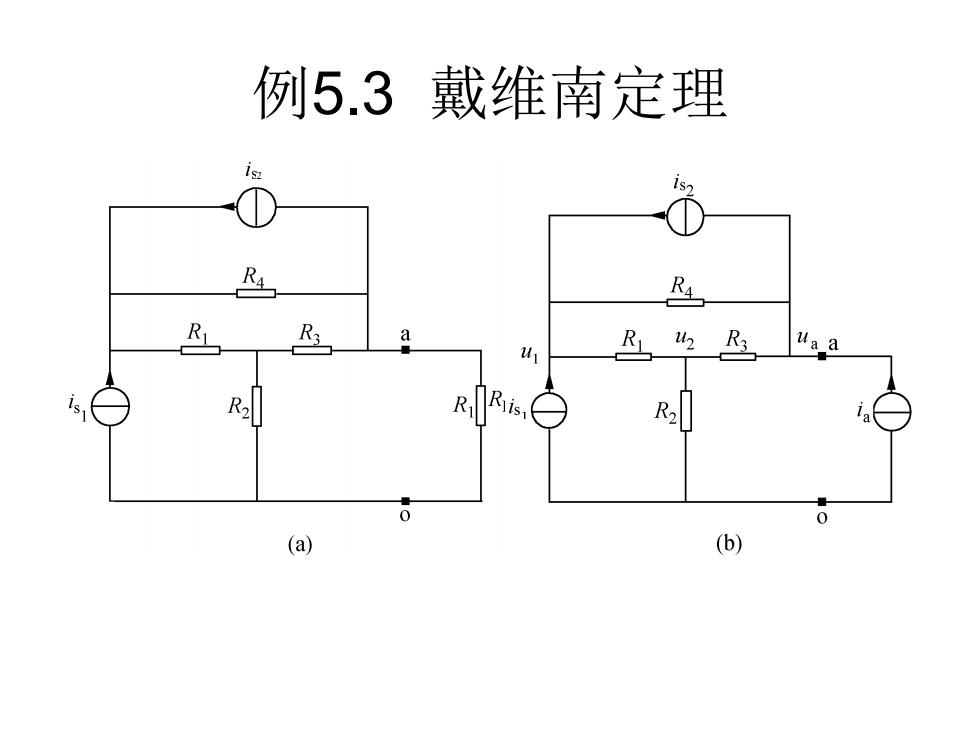
例5.3 戴维南定理 2

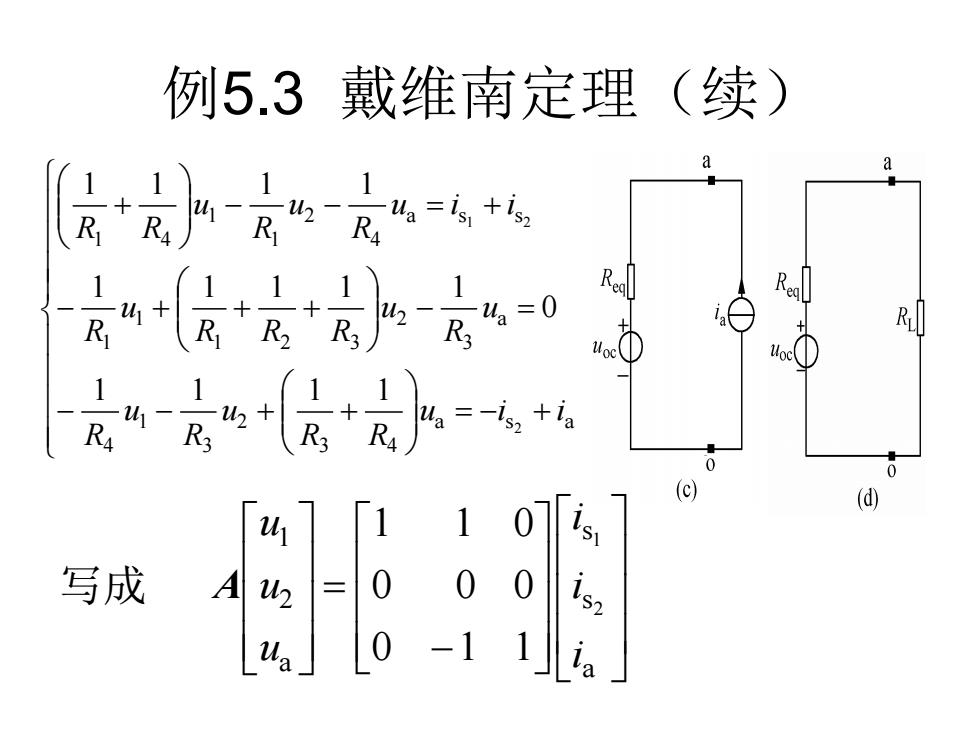
例5.3戴维南定理 （续) a a R R4 R 171 1 Reg R.ea ia R c① 1 0 0 (c) (④ 10 写成 A 40 0 0 07 1

例5.3 戴维南定理（续） 写成            = − +         − − + + − =         − + + + − − = +         + a s a 3 4 2 3 1 4 a 3 2 1 2 3 1 1 a s s 4 2 1 1 1 4 2 1 2 1 1 1 1 0 1 1 1 1 1 1 1 1 1 u i i R R u R u R u R u R R R u R u i i R u R u R R                     − =           a s s a 2 1 2 1 0 1 1 0 0 0 1 1 0 i i i u u u A

例5.4一阶动态电路 2 图5.4-1例5.4的图

例5.4 一阶动态电路 图5.4-1 例5.4的图 R2 i

例5.4一阶动态电路（续) ·第一段： 电压 电流 -初始值 uc(0+)=12V ,0)=40)-1A R2 -稳定值(0)= R is in ()+R3 R3 R2+R 一时常数 RR3C 1=R2+R .uc(t)=uc(oo)+[uc(0+)-uc(oo)]e-t/71 t0 iR(t)=iR(co)+[iR(0+)-iR(co)]e-t/z1 t仑0

例5.4 一阶动态电路（续） • 第一段： 电压 电流 – 初始值 uc(0+)=12V – 稳定值 – 时常数 • uc(t )=uc()+[uc(0+)-uc()]e-t/1 t≥0 • iR(t)=iR()+[iR(0+)-iR()]e-t/1 t≥0 1A (0 ) (0 ) 2 c R2 = = − + + R u i s 2 3 3 R ( ) 2 i R R R i +  = C R R R R 2 3 2 3 1 +  = s 2 3 2 3 c ( ) i R R R R u +  =

例5.4一阶动态电路（续) ·第二段： 电压 电流 -时常数 RR3C, T2-R+R3 .()=12.24en, 0剡t10 u）鼷(10+）-u.(?)e罗， 10,t 3 t10

例5.4 一阶动态电路（续） • 第二段： 电压 电流 – 时常数 , 1 3 1 3 2 C R R R R +  = 12 24 , 0 10 ( ) ( ) (10 ) ( ) , 10 t t c c c c e t u t u u u e t   = 1 10 2 - - - + ìï ï ï ï - í ï ï ï ⅱ? - ? 轾 ïî 臌 剟 „          = 3 10 1 2e 0≤ ≤10 3 0 ( ) 1 - R2 t t t i t t  -

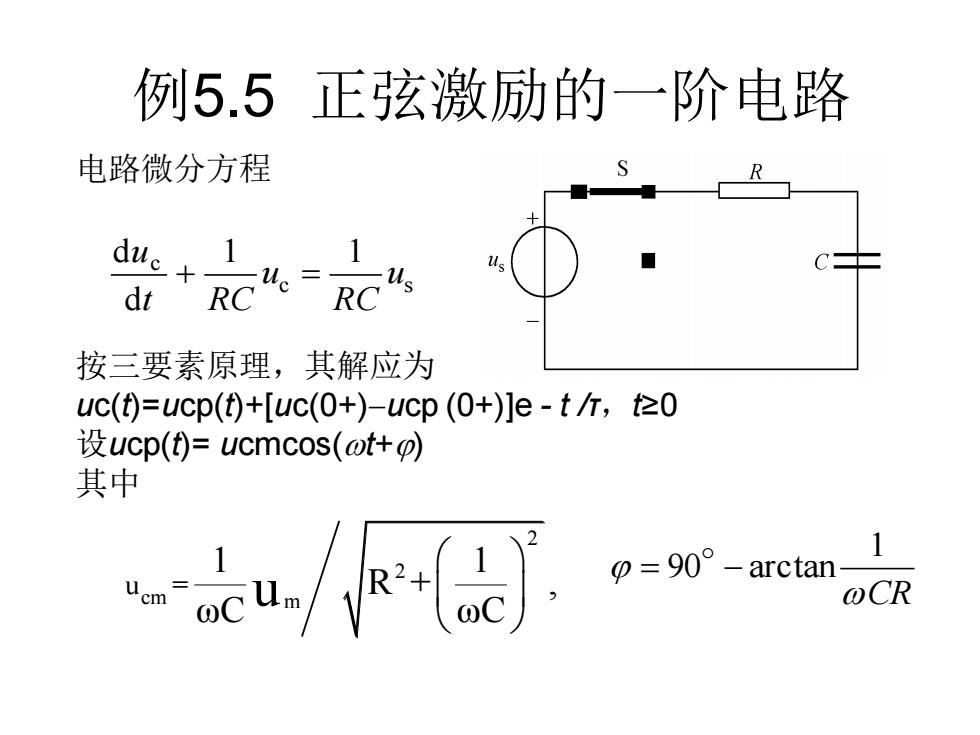
例5.5 正弦激励的一阶电路 电路微分方程 dt RC 。= 按三要素原理，其解应为 uc()=ucp(t)+[uc(0+)-ucp(0+)le-t斤，te0 设ucp()=ucmcos(ot+p) 其中 =90°-arctan- 1 @CR

例5.5 正弦激励的一阶电路 c s c 1 1 d d u RC u t RC u + = 电路微分方程 按三要素原理，其解应为 uc(t)=ucp(t)+[uc(0+)−ucp (0+)]e - t /τ，t≥0 设ucp(t)= ucmcos(t+) 其中 2 2 cm m u = 1 1 R + , ωC ωC u       CR  1 = 90 − arctan 

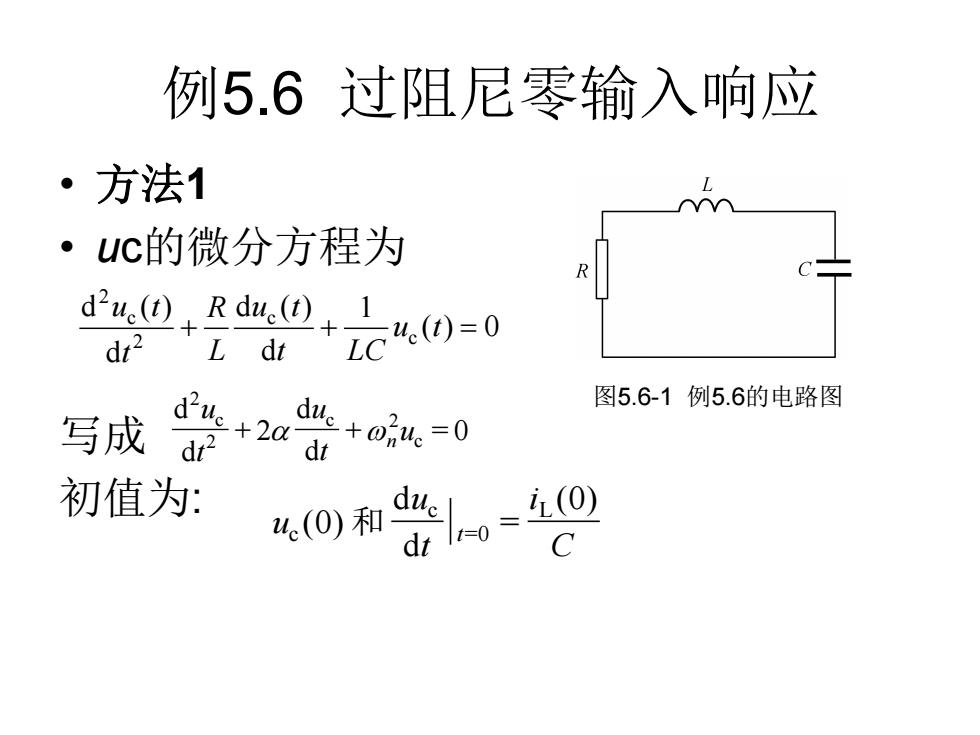
例5.6过阻尼零输入响应 ·方法1 ·uc的微分方程为 du()R due() dt2 L dt i LC.()=0 写成 due +2a de+o24。=0 图5.6-1例5.6的电路图 初值为： 0和监-9

例5.6 过阻尼零输入响应 • 方法1 • uc的微分方程为 写成 初值为: 图5.6-1 例5.6的电路图 ( ) 0 1 d d ( ) d d ( ) c c 2 c 2 + + u t = t LC u t L R t u t + = 0 d d + 2 d d c c 2 2 c 2 u t u t u  n C i t u u t (0) = d d (0) L =0 c c 和