
第6章在普通物理中的应用
第6章 在普通物理中的应用

【例6-1-1】温度单位转换 ·命题:写出一个程序,能把用户输入的摄氏温度转为华氏, 也可反求。 ·解:◆建模 ·两种温度之间的转换公式为: 。摄氏变华氏 9 Tout =Tin+32 5 ·华氏变摄氏 Tom=(n-32)月 ·程序中要先考虑由用户选择转换的方向,再给数据
【例6-1-1】温度单位转换 • 命题:写出一个程序,能把用户输入的摄氏温度转为华氏, 也可反求。 • 解:◆建模 • 两种温度之间的转换公式为: • 摄氏变华氏 • 华氏变摄氏 • 程序中要先考虑由用户选择转换的方向,再给数据。 9 32 5 Tout Tin 5 32 9 Tout Tin

程序exn611 k=inpute(选择1:摄氏变华氏;选择2:华氏变摄氏;. 键入数字1或2:); ·Tin=input(('输入待变换的温度(允许输入数组):) if k==1 Tout Tin*9/5 +32; %摄氏转华氏 elseif k==2 Tout =(Tin-32)*5/9; %华氏转摄氏 ·else disp('未给转换方向,转换无效) 。end ·s=['华氏';'摄氏门; ·s1=['转换后的温度为',s(k,),num2str(Tout),'度'], %注意此语句的编写方法
程序exn611 k = input('选择1:摄氏变华氏;选择2:华氏变摄氏;… 键入数字1或2: '); • Tin = input('输入待变换的温度(允许输入数组):') ; • if k==1 Tout = Tin*9/5 +32; % 摄氏转华氏 • elseif k==2 Tout = (Tin-32)*5/9; % 华氏转摄氏 • else disp('未给转换方向,转换无效'), • end • s = ['华氏';'摄氏']; • s1 = ['转换后的温度为' ,s(k,:),num2str(Tout), '度'], • % 注意此语句的编写方法

【例6-1-2】多种单位间的换算 ·写出一个程序,能把用户输入的长度单位在厘米、 米、千米、英寸、英尺、英里、市尺、市里之间 任意转换。 ·解:◆建模 ·这里采取的技巧是分成两步,先把输入量变换为 米,第二步再把米变换为输出单位,另外,把变 换常数直接表示为一个数组,选择单位的序号也 就成了数组的下标;这样程序就比较简明易读。 程序如下:
【例6-1-2】多种单位间的换算 • 写出一个程序,能把用户输入的长度单位在厘米、 米、千米、英寸、英尺、英里、市尺、市里之间 任意转换。 • 解:◆建模 • 这里采取的技巧是分成两步,先把输入量变换为 米,第二步再把米变换为输出单位,另外,把变 换常数直接表示为一个数组,选择单位的序号也 就成了数组的下标;这样程序就比较简明易读。 程序如下:

长度单位换算程序ex612.m clear all;disp('长度单位换算程序) ·fprintf('长度单位:n);%选择输入输出的单位 。 fprintf(1)厘米2)米3)千米4)英寸n); ·fprintf(5)英尺6)英哩7)市尺8)市里n): ·InUnits=inpute('选择输入单位编号:"); ·OutUnits=input(选择输出单位编号:); ·9 %令各种单位对米的变换常数数组为ToMeter ·ToMeter=[0.01,1.00,1000.0,0.0254,0.3048, 1609.3,1/3,500];
长度单位换算程序ex612.m clear all; disp(' 长度单位换算程序') • fprintf('长度单位: \n'); % 选择输入输出的单位 • fprintf(' 1) 厘米 2) 米 3) 千米 4) 英寸 \n'); • fprintf(' 5) 英尺 6) 英哩 7) 市尺 8) 市里 \n'); • InUnits = input('选择输入单位编号: '); • OutUnits = input('选择输出单位编号: '); • % 令各种单位对米的变换常数数组为ToMeter • ToMeter = [0.01, 1.00, 1000.0, 0.0254, 0.3048, 1609.3, 1/3, 500 ];

程序ex612.m(续) FrmMeter=1./ToMeter; Value=input('输入待变换的值(O为退出):); while(Value ~=0) ValueinM Value*ToMeter(InUnits); %把输入值变为米 New alue ValueinM*FrmMeter(OutUnits); %把米变为输出单位 fprintf(变换后的值是%gn',NewValue); %打印变换后的值 Value=input('输入待变换的值(O为退出):); %提问下个输入值 end
程序ex612.m(续) FrmMeter= 1./ ToMeter; Value = input('输入待变换的值(0为退出): '); while( Value ~= 0 ) ValueinM = Value*ToMeter(InUnits); % 把输入值变为米 NewValue = ValueinM*FrmMeter(OutUnits); % 把米变为输出单位 fprintf('变换后的值是 %g \n' ,NewValue); % 打印变换后的值 Value = input('输入待变换的值(0为退出): '); % 提问下个输入值 end

【例6-1-3】实验数据拟合 命题:设在某一实验中,给某元件加[1,2,3,4,5V电压,测得 的电流为[0.2339,0.3812,0.5759,0.8153,0.97421ma。 求此元件的电阻。 解:◆建模 ·模型:设直线的方程为y=a(1)x+a(2),待定的系数是 a(1),a(2)。将上述数据分别代入x,y, ·a(1)+a(2)=0.2339 17 1 0.2339 ·2a(1)+a(2)=0.3812 2 1 0.3812 ·3a(1)+a(2)=0.5759 → 3a(1)+1a(2)F 0.5759 ·4a(1)+a(2)=0.8153 4 1 0.8153 ·5a(1)+a(2)=0.9742 5 0.9742 ·把这五个方程联立,用矩阵表述,得 datax *a(1)+ones(N,1)*a(2)=datay
【例6-1-3】实验数据拟合 命题:设在某一实验中,给某元件加[1,2,3,4,5]v电压,测得 的电流为[ 0.2339, 0.3812, 0.5759, 0.8153, 0.9742 ]ma。 求此元件的电阻。 解:◆ 建模 • 模型:设直线的方程为 y= a(1)x +a(2), 待定的系数是 a(1),a(2)。将上述数据分别代入x,y, • a(1)+a(2)=0.2339 • 2a(1)+a(2)=0.3812 • 3a(1)+a(2)=0.5759 • 4a(1)+a(2)=0.8153 • 5a(1)+a(2)=0.9742 • 把这五个方程联立,用矩阵表述, 得 • datax *a(1) + ones(N,1) * a(2) = datay 1 1 0.2339 2 1 0.3812 3 a(1) 1 a(2)= 0.5759 4 1 0.8153 5 1 0.9742
程序exn613 ·这是一个超定方程组,写成A*a=B,其最小二乘解可以 用左除运算符a=A1B来求得。因此程序如下: ·lear,datax=[1:5]'; ·datay=[0.2339,0.3812,0.5759,0.8153,0.9742] A=[datax,ones(5,1)];B=datay; ·a=A1B,r=1/a(1) plot(datax,datay,'o'),hold on 0.8 ·运行结果为: 0.6 ·a(1)=0.1905 0.4 ·a(2)=0.0247 0.2 ·画出曲线如右图。 0 4 6
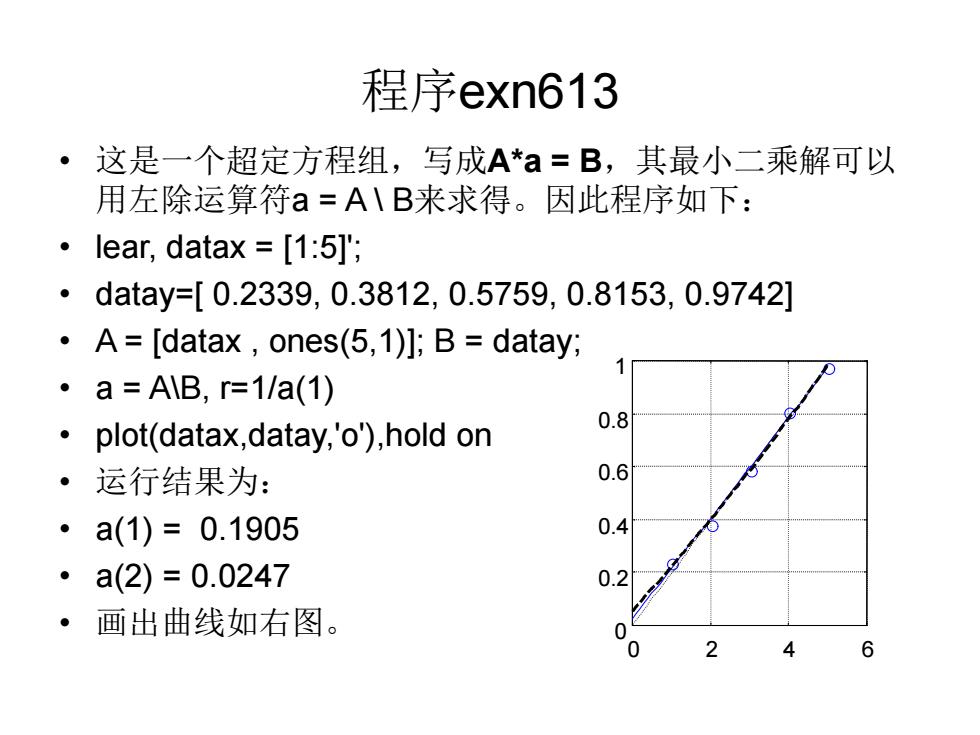
程序exn613 • 这是一个超定方程组,写成A*a = B,其最小二乘解可以 用左除运算符a = A \ B来求得。因此程序如下: • lear, datax = [1:5]'; • datay=[ 0.2339, 0.3812, 0.5759, 0.8153, 0.9742] • A = [datax , ones(5,1)]; B = datay; • a = A\B, r=1/a(1) • plot(datax,datay, 'o'),hold on • 运行结果为: • a(1) = 0.1905 • a(2) = 0.0247 • 画出曲线如右图。 0 2 4 6 0 0.2 0.4 0.6 0.8 1

6.2力学基础 ·【例6-2-1】目标相对于射点的高度为y,给定初速和射角, 计算物体在真空中飞行的时间和距离。 ·◆建模:这里目标和射点不在同一高度上,不好求封闭 形式的解,用MATLAB使整个计算和绘图过程自动化。其 好处是可快速地计算其在不同初速和射角下的飞行时间和 距离。关键在求落点时间t时需要解一个二次线性代数方 程 由y=votsin。 28 ● 解出t,她就是落点时间tf。它会有两个解,我们只取其中 一个有效解。再求 mYofr sino
6.2 力学基础 • 【例6-2-1】目标相对于射点的高度为 yf,给定初速和射角, 计算物体在真空中飞行的时间和距离。 • ◆建模:这里目标和射点不在同一高度上,不好求封闭 形式的解,用MATLAB使整个计算和绘图过程自动化。其 好处是可快速地计算其在不同初速和射角下的飞行时间和 距离。关键在求落点时间tf时需要解一个二次线性代数方 程 • 由 • • 解出t,她就是落点时间tf。它会有两个解,我们只取其中 一个有效解。再求 2 0 0 f 1 sin 2 y v t gt y max 0 f 0 x v t sin

程序eXn621 ·clear;y0=0;x0=0; %初始位置 vMag=input('输入初始速度(mls):);%输入初始速度 ·vDir=input(输入初速方向(度):); ·yf=input('输入目标高度(米):); %输入目标高度yh ·Vx0=vMag*cos(vDir*(pi/180);%计算x,y方向的初速 vy0 VMag*sin(vDir*(pi/180)); ·Wy=-9.81;wx=0; %重力加速度(m/s2) 。 tf=roots(wy/2,y0,y0-y);%解代数方程计算落点tf ·tf=max(tf; %去除tf两个解中的庸解 ·t=0:0.1:tf ·y=y0+y0*t+y*t.2/2; %计算轨迹 ·X=x0+VX0*t+Wx*t.2/2; xf max(x),plot(x,y), %计算射程,画出轨迹
程序exn621 • clear; y0 = 0; x0 = 0; % 初始位置 • vMag = input('输入初始速度 (m/s): '); % 输入初始速度 • vDir = input(' 输入初速方向(度): '); • yf = input('输入目标高度(米): '); % 输入目标高度yh • vx0 = vMag*cos(vDir* (pi/180)); % 计算x,y方向的初速 • vy0 = vMag*sin(vDir* (pi/180)); % • wy = -9.81; wx = 0; % 重力加速度 (m/s^2) • tf=roots([wy/2,vy0,y0-yf]); % 解代数方程计算落点tf • tf=max(tf); % 去除tf两个解中的庸解 • t=0:0.1:tf; • y = y0 + vy0*t + wy*t.^2/2; % 计算轨迹 • x = x0 + vx0*t + wx*t.^2/2; • xf = max(x),plot(x,y), % 计算射程,画出轨迹