
第六章用行阶梯法解方程组
第六章 用行阶梯法解方程组

6.1方程的MATLAB表示方法 A*x=b a(1,1)a(1,2)… a(1,n) x(1) b(1) 其中: A= a(2,1)a(2,2)· a(2,n) x(2) b(2) x= b= a(m,1)a(m,2)…a(m,n) x(n) b(m) 等价于「a(1,1)*x(1)+a(1,2)*x(2)+…+a(1,n)*x(n) b(1) a(2,1)*x(1)+a(2,2)*x(2)+…+a(2,n)*x(n) b(2) … … a(m,1)*x(1)+a(m,2)*x(2)+…+a(m,n)*x(n) b(m)
6.1 方程的MATLAB表示方法 其中: 等价于 A x b * = (1,1) (1,2) (1, ) (1) (1) (2,1) (2,2) (2, ) (2) (2) , , ( ,1) ( ,2) ( , ) ( ) ( ) a a a n x b a a a n x b A x b a m a m a m n x n b m = = = (1,1)* (1) (1,2)* (2) (1, )* ( ) (1) (2,1)* (1) (2,2)* (2) (2, )* ( ) (2) ( ,1)* (1) ( ,2)* (2) ( , )* ( ) ( ) a x a x a n x n b a x a x a n x n b a m x a m x a m n x n b m + + + + + + = + + +

行号、列号和变量名 。 可以看出,变量后圆括号中的第一个数是行号, 第二个数是列号,不加下标的变量A自身代表 一个矩阵。除了把下标放入圆括号中之外, MATLAB的表述与原来的算式是完全一致的, 非常好记。不过在MATLAB中变量名和元素名 是一致的,式(6.3)中的矩阵A应该是a。但是为 了使叙述文与一般的矩阵书籍相一致,我们还 是把矩阵用大写字母表示,数组和元素则用小 写字母,希望读者注意
行号、列号和变量名 • 可以看出,变量后圆括号中的第一个数是行号, 第二个数是列号,不加下标的变量A自身代表 一个矩阵。除了把下标放入圆括号中之外, MATLAB的表述与原来的算式是完全一致的, 非常好记。不过在MATLAB中变量名和元素名 是一致的,式(6.3)中的矩阵A应该是a。但是为 了使叙述文与一般的矩阵书籍相一致,我们还 是把矩阵用大写字母表示,数组和元素则用小 写字母,希望读者注意

欠定、适定和超定方程 如果n是未知数的数目,m是独立方程的数目, 那么当n>m时,未知数比独立方程数日多,此 方程组有无数个解,称为欠定方程;当n<m时, 未知数比独立方程数目少,此方程组无解,称 为超定方程;只有当n=m时,未知数与独立方 程数目相等,因而有惟一的解x,称为适定方 程。所以,不能简单地看形式上的m和n,还必 须要剔除其中非独立方程的虚假成分。本章和 下一章中将讨论的行阶梯形式、行列式和‘秩’ 等概念,很大程度上就是为了找到独立方程的 数日
欠定、适定和超定方程 • 如果n是未知数的数目,m是独立方程的数目, 那么当nm时,未知数比独立方程数目多,此 方程组有无数个解,称为欠定方程;当nm时, 未知数比独立方程数目少,此方程组无解,称 为超定方程;只有当n=m时,未知数与独立方 程数目相等,因而有惟一的解x,称为适定方 程。所以,不能简单地看形式上的m和n,还必 须要剔除其中非独立方程的虚假成分。本章和 下一章中将讨论的行阶梯形式、行列式和‘秩’ 等概念,很大程度上就是为了找到独立方程的 数目

几种二元线性方程的解 ·例6.1求解下列四个线性方程组 (a)x1-2x2=-1 (b) x1-2x2=-1 -X1+3x2=3 -X1+2x2=3 (C)x1-2x2=-1 (d) x1+x2=1 -X1+2x2=1 X1-X2=3 -x1+2x2=-3
几种二元线性方程的解 • 例6.1 求解下列四个线性方程组 • (a) (b) • (c) (d) 1 2 1 2 2 = -1 3 = 3 x x x x − − + 1 2 1 2 2 = -1 2 = 3 x x x x − − + 1 2 1 2 2 = -1 2 = 1 x x x x − − + 1 2 1 2 1 2 = 1 = 3 2 =-3 x x x x x x + − − +
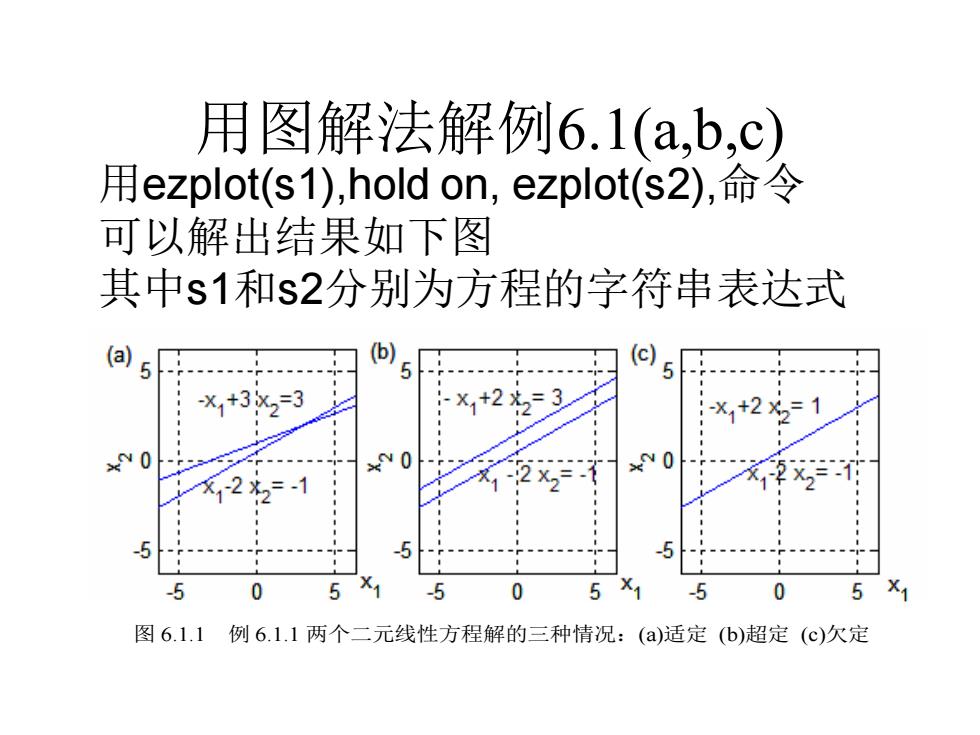
用图解法解例6.1(a,b,c) 用ezplot(s1),hold on,ezplot(s2),命令 可以解出结果如下图 其中s1和s2分别为方程的字符串表达式 (a5 (b) (c) %1+3x2=3 :X1+2光=3 :+2X2=1 ×N0 r 12X=-1 5 5 0 5X1 -5 0 5X1 5 5×1 图6.1.1例6.1.1两个二元线性方程解的三种情况:(a)适定(b)超定(c)欠定
用图解法解例6.1(a,b,c) 图 6.1.1 例 6.1.1 两个二元线性方程解的三种情况:(a)适定 (b)超定 (c)欠定 用ezplot(s1),hold on, ezplot(s2),命令 可以解出结果如下图 其中s1和s2分别为方程的字符串表达式
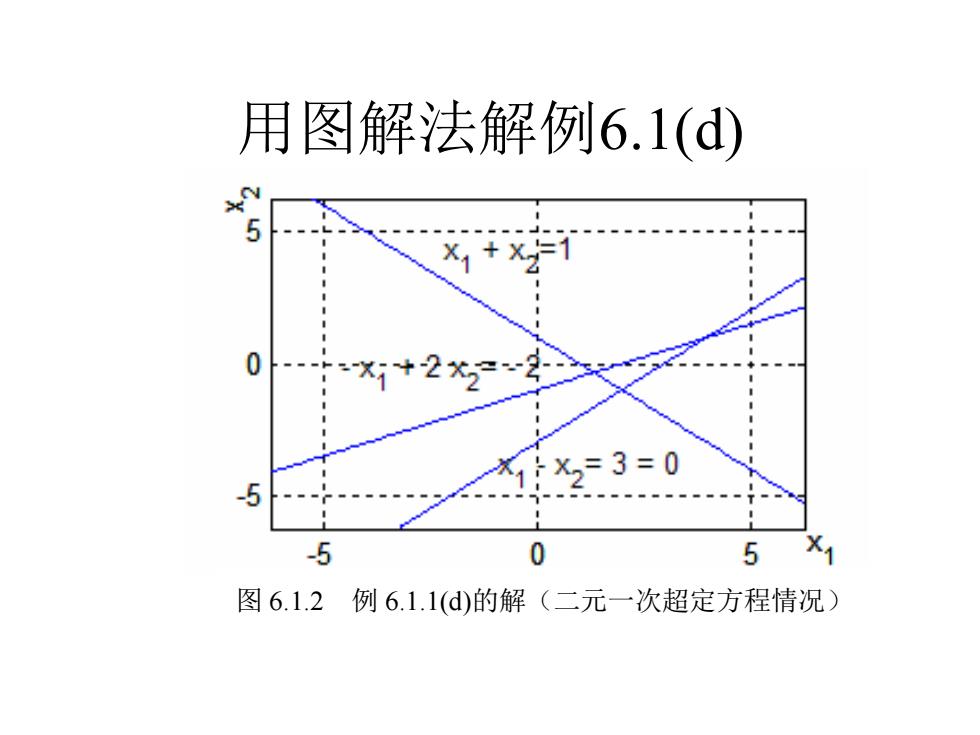
用图解法解例6.1(d) 1X2=3=0 5 0 5 X 图6.1.2例6.1.1(d)的解(二元一次超定方程情况)
用图解法解例6.1(d) 图 6.1.2 例 6.1.1(d)的解(二元一次超定方程情况)

用解析法解例6.1.1 ·用代入法或消去法等中学方法求解; ·用矩阵求解的方法 ·用MATLAB符号工具箱求解[xla,x2a=solve(sl,s2) 其结果当然是相同的: (a)解为xla=3,x2a=2 (b)解为x1b-[],x2b=[], 表示无解 (c)解为xlc=2*x2-1,x2c-x2, 表示有无数解 (d)解为x1d=[],x2d=[], 表示无解
用解析法解例6.1.1 • 用代入法或消去法等中学方法求解; • 用矩阵求解的方法 • 用MATLAB符号工具箱求解[x1a,x2a]=solve(s1,s2) 其结果当然是相同的: (a) 解为x1a=3,x2a=2 (b) 解为x1b=[ ],x2b=[ ], 表示无解 (c) 解为x1c=2*x2-1,x2c=x2, 表示有无数解 (d) 解为x1d=[ ],x2d=[ ], 表示无解

求解三元线性方程组的例 x y-z=5 2*x-3*y+Z=3 (由1,2式消去z)3*x-2*y=8 -5*x+2*y-2*z=0(由2,3式消去2)-x-4*y=6 ·再由两式联立解得: x=1.4286y=-1.8571z=-5.4286 用图解方法ezplplot3画此三个方程的平面, 用的就是例5.3的程序,得到:
求解三元线性方程组的例 → • 再由两式联立解得: x=1.4286 y=-1.8571 z=-5.4286 用图解方法ezplplot3画此三个方程的平面, 用的就是例5.3的程序,得到: x + y - z = 5 2*x - 3*y + z = 3 -5*x+2*y-2*z = 0 ( 1,2 z) 3*x - 2*y=8 ( 2,3 z) - x - 4*y =6 由 式消去 由 式消去
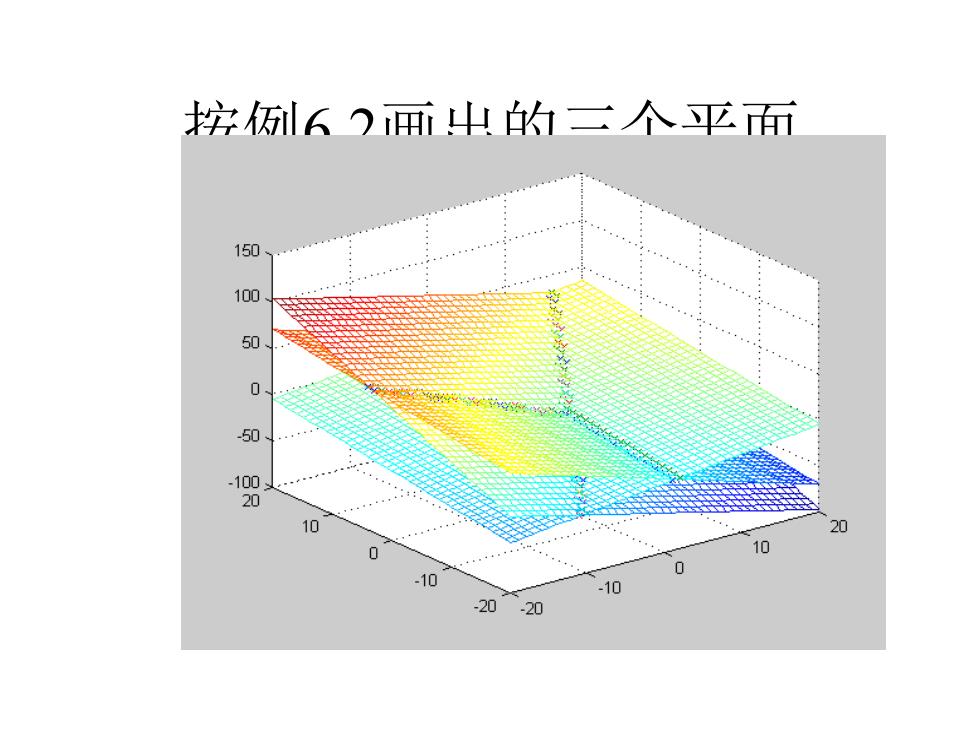
按6)两出的二个平而 150 100 50 50 .100 10 20 10 .10 -10 -20 -20
按例6.2画出的三个平面