
第7章在力学机械中的应用
第7章 在力学机械中的应用

7.1理论力学 例7-1-1任意平面力系的简化 ·本程序可用来对任意多个力组成的平面力 系作简化,得出一个合力,分成两步做: ·第一步:向任意给定点p0简化,得到一个 主向量和一个主矩; ·第二步,将此主矩和主向量转换成一个合 力。程序如下:
7-1 理论力学 例7-1-1 任意平面力系的简化 • 本程序可用来对任意多个力组成的平面力 系作简化,得出一个合力,分成两步做: • 第一步:向任意给定点p0简化,得到一个 主向量和一个主矩; • 第二步,将此主矩和主向量转换成一个合 力。程序如下:

程序exn711 clear,N=inpute('输入力的数目N=)%输入力系的数据 for i=1:N i,f,:)=input((力f0)的x,y两个分量fx(0),fy(0]=): p(i,:)=input('力f0的一个作用点的坐标p()=[px,py]="); end p0=input('简化转移点p0的坐标p0=[p0x,pOy]=): ft=sum(f), %求主向量 for i=1:N %计算各力对p0点的力矩 m(0)=fi,2)*(p(i,1)-p0(1)-f0,1)*(p(i,2)-p0(2); end mt=sum(m) %相加求主矩 pt=mt/[ft(2);-ft(1)】+p0 %求合力作用点的坐标
程序exn711 clear, N=input('输入力的数目N=') %输入力系的数据 for i=1:N i, f(i,:)=input('力f(i)的x,y两个分量[fx(i),fy(i) ] = '); p(i,:)=input('力f(i)的一个作用点的坐标p(i)= [px,py ] = '); end p0=input('简化转移点p0的坐标p0= [p0x,p0y ] = '); ft=sum(f), % 求主向量 for i=1:N %计算各力对p0点的力矩 m(i)=f(i,2)*(p(i,1)-p0(1))-f(i,1)*(p(i,2)-p0(2)); end mt=sum(m) % 相加求主矩 pt = mt/ [ft(2);-ft(1)] + p0 % 求合力作用点的坐标

程序exn711运行结果 ·最后一行程序是基于下列求合力作用点坐标 [pt(1),pt(2)]的方程: t(2)*(p0(1)-pt(1)-ft(1)*(p0(2)-pt(2)+mt=0 可写成(pt-p0)*[t(2);-t(1)】=-mt,再转成程序中的 p0表达式。由于是一个方程求两个未知数,这是 一个不定方程,用矩阵右除的方法将给出无数个 解中之一,即ptp0中有一个分量是零。 。 运行此程序,设N=3,f(1)=[2,3],p(1)=[-1,0],f(2) =[4,7],p(2)=[1,-2],f3)=[3,-4],p(3)=[1,2],又设 简化点的坐标p0=【-1,-1],答案为: 。ft=[161,mt=-9,pt=[-2.5000-1.00001
程序exn711运行结果 • 最后一行程序是基于下列求合力作用点坐标 [pt(1),pt(2)]的方程: ft(2)*(p0(1)-pt(1))- ft(1)*(p0(2)-pt(2)) + mt =0 可写成(pt-p0)* [ft(2); -ft(1)] = -mt, 再转成程序中的 p0表达式。由于是一个方程求两个未知数,这是 一个不定方程,用矩阵右除的方法将给出无数个 解中之一,即pt-p0中有一个分量是零。 • 运行此程序,设N=3,f(1)= [2,3],p(1) = [-1,0], f(2) = [-4,7],p(2)= [1,-2],f(3) = [3,-4], p(3)= [1,2],又设 简化点的坐标p0= [-1,-1],答案为: • ft =[ 1 6 ], mt = -9, pt =[ -2.5000 -1.0000]
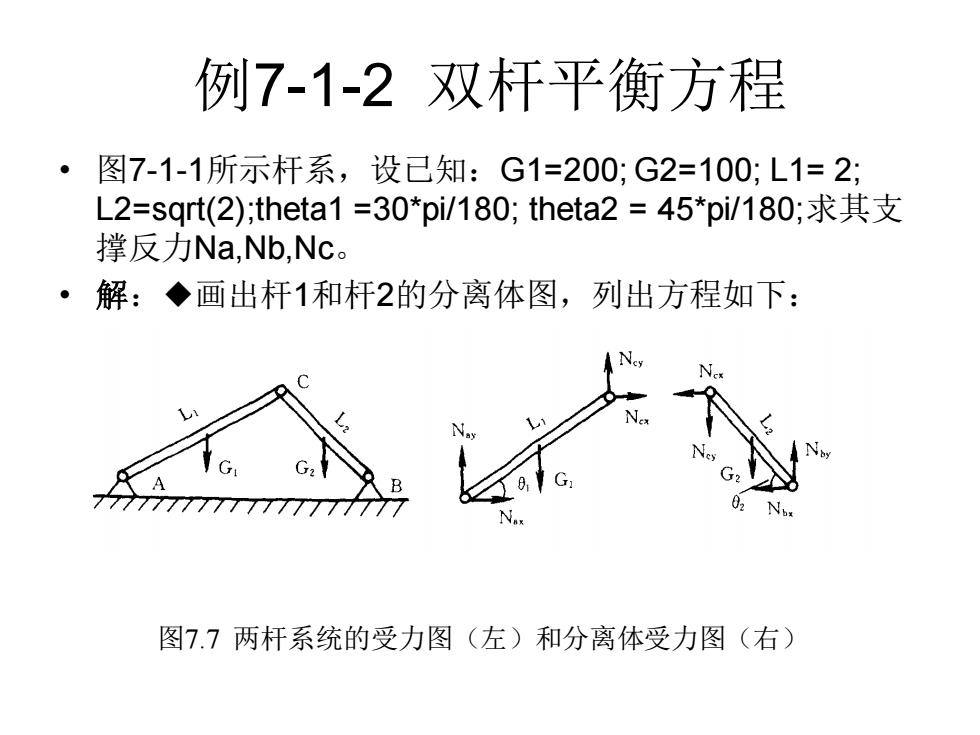
例7-1-2双杆平衡方程 ·图7-1-1所示杆系,设已知:G1=200;G2=100;L1=2; L2=sqrt(2);theta1=30*pi/180;theta2=45*pi/180;求其支 撑反力Na,Nb,Nc。 ·解:◆画出杆1和杆2的分离体图,列出方程如下: 02N 图7.7两杆系统的受力图(左)和分离体受力图(右)
例7-1-2 双杆平衡方程 • 图7-1-1所示杆系,设已知:G1=200; G2=100; L1= 2; L2=sqrt(2);theta1 =30*pi/180; theta2 = 45*pi/180;求其支 撑反力Na,Nb,Nc。 • 解:◆画出杆1和杆2的分离体图,列出方程如下: 图7.7 两杆系统的受力图(左)和分离体受力图(右)

线性数学模型 对杆件1:∑X=0Nax+Ncx=0 ∑Y=0Nay+Ncy-G1=0; ZM=0 Ncy*L1*cos(theta1)-Ncx*L1*sin(theta1)-... G1*L1/2*cos(theta1)=0; 对杆件2:ΣX=0Nbx-Ncx=0; ΣY=0Nby-Ncy-G2=0; ZM=0 Ncy*L2*cos(theta2)+ Ncx*L2*sin(theta2)+G2*L2/2*cos(theta2)=0; 这是一组包含六个未知数Nax,Nay,Nbx,Nby,Ncx,Ncy的六 个线性代数方程,通常是要寻找简化的方法,但用了 MATLAB工具,就可以列出矩阵方程AX=B,(其中 X=[Nax,Nay,Nbx,Nby,Ncx,NcyT,,可用矩阵除法直接来解
线性数学模型 对杆件1:ΣX=0 Nax + Ncx = 0 ΣY=0 Nay + Ncy - G1 = 0; ΣM=0 Ncy*L1*cos(theta1)-Ncx*L1*sin(theta1)-… G1*L1/2*cos(theta1)=0; 对杆件2: ΣX=0 Nbx - Ncx = 0; ΣY=0 Nby - Ncy - G2 = 0; ΣM=0 Ncy*L2*cos(theta2)+ … Ncx*L2*sin(theta2)+G2*L2/2*cos(theta2)=0; 这是一组包含六个未知数Nax, Nay, Nbx, Nby, Ncx, Ncy的六 个线性代数方程,通常是要寻找简化的方法,但用了 MATLAB工具,就可以列出矩阵方程AX=B,(其中 X=[Nax,Nay,Nbx,Nby,Ncx,Ncy]T,可用矩阵除法直接来解

程序exn712 %给原始参数赋值 G1=200;G2=100;L1=2;L2=sqt(2); %将度化为弧度 theta1 =30*pi/180;theta2 =45*pi/180; %则按此次序,系数矩阵A,B可写成下式 A=[1,0,0,0,1,0;0,1,0,0,0,1;0,0,0,0,-sin(theta1), c0s(theta1);0,0,1,0,-1,0;0,0,0,1,0,-1;. 0,0,0,0,sin(theta2),cos(theta2)] B=[0;G1;G1/2*cos(theta1);0;G2;-G2/2*cos(theta2)] X=AlB; %用左除求解线性方程组
程序exn712 %给原始参数赋值 G1=200; G2=100; L1= 2; L2 = sqrt (2) ; % 将度化为弧度 theta1 =30*pi/180; theta2 = 45*pi/180; % 则按此次序,系数矩阵A,B可写成下式 A=[1,0,0,0,1,0;0,1,0,0,0,1;0,0,0,0,-sin(theta1),... cos(theta1); 0,0,1,0,-1,0;0,0,0,1,0,-1;... 0,0,0,0, sin(theta2),cos(theta2)] B=[0;G1;G1/2*cos(theta1);0;G2;-G2/2*cos(theta2)] X = A\B; %用左除求解线性方程组
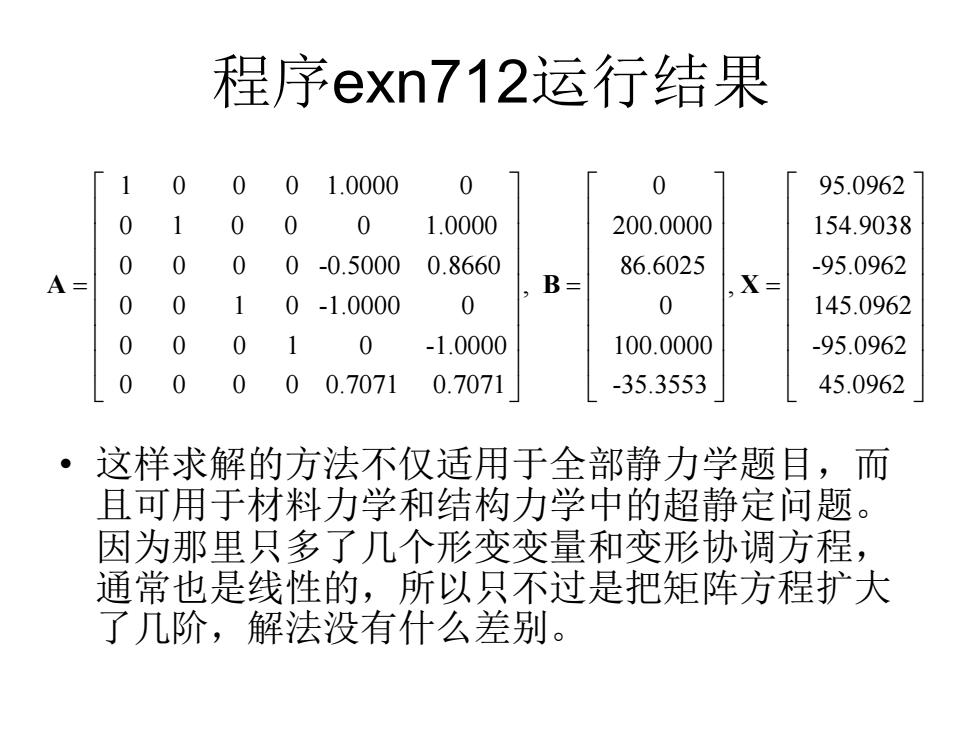
程序exn712运行结果 1 0 0 0 1.0000 0 0 95.0962 0 1 0 0 0 1.0000 200.0000 154.9038 0 0 0 0-0.5000 0.8660 86.6025 -95.0962 B= ,X= 0 0 1 0-1.0000 0 0 145.0962 0 0 0 0 -1.0000 100.0000 -95.0962 0 0 00.7071 0.7071 -35.3553 45.0962 这样求解的方法不仅适用于全部静力学题目,而 且可用于材料力学和结构力学中的超静定问题。 因为那里只多了几个形变变量和变形协调方程, 通常也是线性的,所以只不过是把矩阵方程扩大 了几阶,解法没有什么差别
程序exn712运行结果 • 这样求解的方法不仅适用于全部静力学题目,而 且可用于材料力学和结构力学中的超静定问题。 因为那里只多了几个形变变量和变形协调方程, 通常也是线性的,所以只不过是把矩阵方程扩大 了几阶,解法没有什么差别。 1 0 0 0 1.0000 0 0 1 0 0 0 1.0000 0 0 0 0 -0.5000 0.8660 0 0 1 0 -1.0000 0 0 0 A = 0 95.0962 200.0000 154.903 86.6025 , , 0 0 1 0 -1.0000 100.0000 0 0 0 0 0.7071 0.7071 -35.3553 = = B X 8 -95.0962 145.0962 -95.0962 45.0962
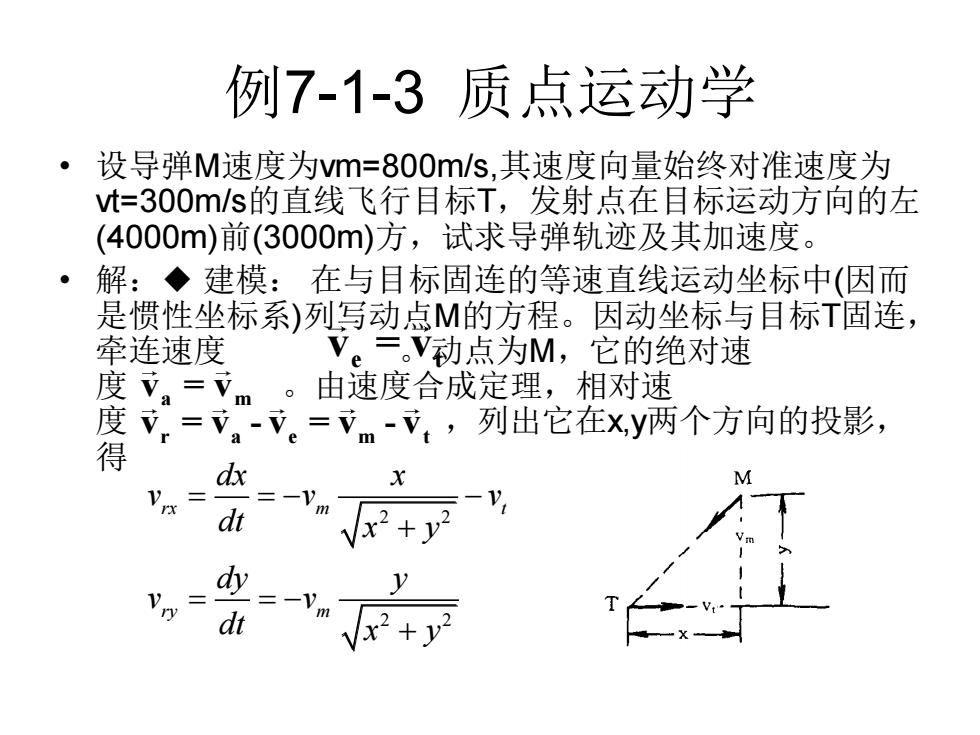
例7-1-3质点运动学 ·设导弹M速度为vm=800m/s,其速度向量始终对准速度为 t=300m/s的直线飞行目标T,发射点在目标运动方向的左 (4000m)前(3000m)方,试求导弹轨迹及其加速度。 ·解:◆建模:在与目标固连的等速直线运动坐标中(因而 是惯性坐标系)列写动点M的方程。因动坐标与目标T固连, 牵连速度 Ve=。V动点为M,它的绝对速 度V。=Vm。由速度合成定理,相对速 度,=,。=m-:,列出它在xy两个方向的投影, d d dt
例7-1-3 质点运动学 • 设导弹M速度为vm=800m/s,其速度向量始终对准速度为 vt=300m/s的直线飞行目标T,发射点在目标运动方向的左 (4000m)前(3000m)方,试求导弹轨迹及其加速度。 • 解:◆ 建模: 在与目标固连的等速直线运动坐标中(因而 是惯性坐标系)列写动点M的方程。因动坐标与目标T固连, 牵连速度 。动点为M,它的绝对速 度 。由速度合成定理,相对速 度 ,列出它在x,y两个方向的投影, 得 e t v = v a m v = v r a e m t v = v - v = v - v 2 2 2 2 rx m t ry m dx x v v v dt x y dy y v v dt x y = = − − + = = − +

主程序exn713 global vt vm vt=input('vt=');vm=input('vm='); %输入共用的参数 z0=input('[x0;y0]=); %输入数值积分需要的参数 tspan=input('tspan=[to,tfinal]=); % [t,z]ODE23('ex713f,tspan,z0); %进行数值积分 plot(z(,1),z:,2): %绘图 %M点位置的导数是相对速度,二次导数则为绝对加速度 dt=diff(t);Ldt=length(dt); %为了求导数先求t的增量 X=Z(:,1)y=Z(:,2); %把z写成xy两个分量形式 vx=diff(z(:,1))./dt;vy=diff(z(:,2))./dt; wx=diff(W./dt(1:Ldt-1);wy=dif(y)./dt(1:Ldt-1);%二次导数 [t(2:Ldt),x(2:Ldt),y(2:Ldt),wx,wy] %显示数据
主程序exn713 global vt vm vt=input('vt=');vm=input('vm='); %输入共用的参数 z0=input('[x0;y0]='); %输入数值积分需要的参数 tspan=input('tspan=[t0,tfinal]='); % [t,z] = ODE23('ex713f',tspan,z0); %进行数值积分 plot(z(:,1),z(:,2)); %绘图 % M点位置的导数是相对速度,二次导数则为绝对加速度 dt=diff(t); Ldt=length(dt); %为了求导数先求t的增量 x=z(:,1);y=z(:,2); % 把z写成x,y两个分量形式 vx=diff(z(:,1))./dt;vy=diff(z(:,2))./dt; % wx=diff(vx)./dt(1:Ldt-1);wy=diff(vy)./dt(1:Ldt-1); %二次导数 [t(2:Ldt),x(2:Ldt),y(2:Ldt),wx,wy] %显示数据