
第二篇线性代数实践 第五章预备知识
第二篇 线性代数实践 第五章 预备知识

5.1实验在线性代数中的重要性 利用软件工具进行实验有以下的一些好处: 。 好处一:对于低价(三阶及以下)的线性 代数问题,MATLAB能提供图形帮助,有利 于牢固地掌握概念。 。 好处二:对于高阶的问题,MATLAB能提供 计算程序,方便而简捷,节省时间。 好处三:由于解题快捷,在课程中可以较 多地放进线性代数的应用实例。扩展学生 的视野,提高学习的目的性和积极性
5.1 实验在线性代数中的重要性 利用软件工具进行实验有以下的一些好处: • 好处一:对于低价(三阶及以下)的线性 代数问题,MATLAB能提供图形帮助,有利 于牢固地掌握概念。 • 好处二:对于高阶的问题,MATLAB能提供 计算程序,方便而简捷,节省时间。 • 好处三:由于解题快捷,在课程中可以较 多地放进线性代数的应用实例。扩展学生 的视野,提高学习的目的性和积极性

“线性代数实践’的预期效果 所以我们敢于提出本书的标志性特征: 。 线性代数抽象吗?看了本书后,你会知道 它的概念都基于空间形象。 。 线性代数冗繁吗?学了本书后,你会懂得 它的计算全可有简明程序。 线性代数枯燥吗?读了本书后,你会发现 它的应用极其广泛又精彩
‘线性代数实践’的预期效果 所以我们敢于提出本书的标志性特征: • 线性代数抽象吗?看了本书后,你会知道 它的概念都基于空间形象。 • 线性代数冗繁吗?学了本书后,你会懂得 它的计算全可有简明程序。 • 线性代数枯燥吗?读了本书后,你会发现 它的应用极其广泛又精彩
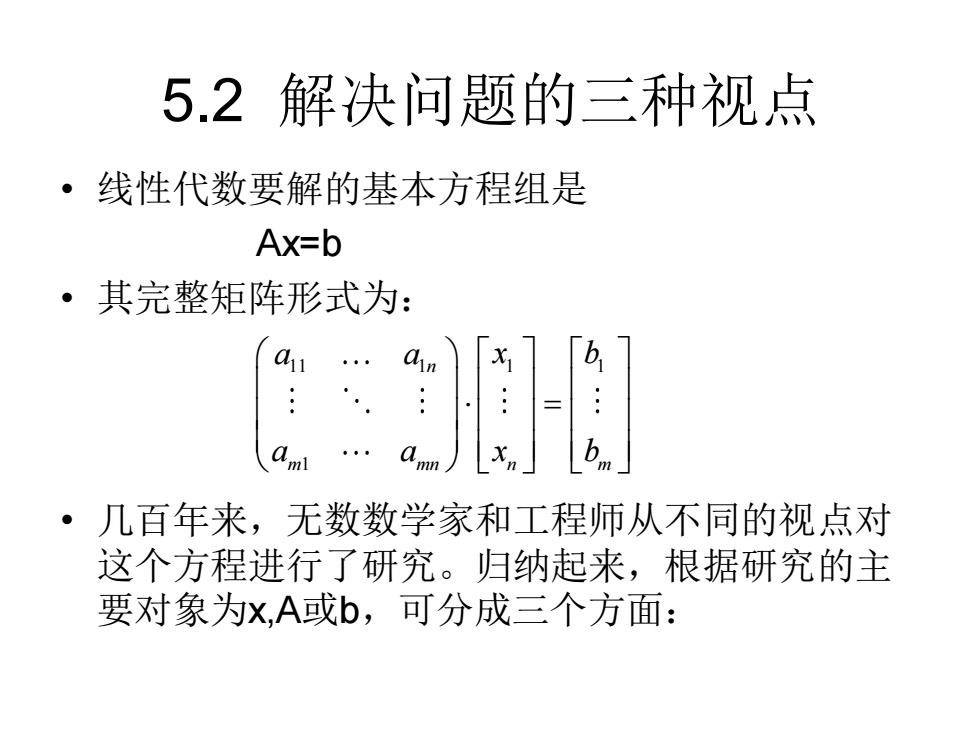
5.2解决问题的三种视点 ·线性代数要解的基本方程组是 Ax=b 。其完整矩阵形式为: am ·几百年来,无数数学家和工程师从不同的视点对 这个方程进行了研究。归纳起来,根据研究的主 要对象为x,A或b,可分成三个方面:
5.2 解决问题的三种视点 • 线性代数要解的基本方程组是 Ax=b • 其完整矩阵形式为: • 几百年来,无数数学家和工程师从不同的视点对 这个方程进行了研究。归纳起来,根据研究的主 要对象为x,A或b,可分成三个方面: 11 1 1 1 1 n m mn n m a a x b a a x b =

从解联立方程的视点 ·视点1:着重研究解x,即研究线性方程组的解法。 中学里做的就是这样,前面介绍的用MATLAB矩 阵除法的解也是如此。 要点:矩阵的每一行代表一个方程,m行代表m 个线性联立方程。n列代表n个变量。如果m是独 立方程数,根据mn确定方程是’欠 定’、’适定’ 还是’超定’。对这三种情况都 会求解了,研究就完成了。 必须剔除非独立方程。.行阶梯形式、行列式和秩的 概念很大程度上为此目的而建立。 本书6,7两章对应于本视点,区别是第6章用行阶梯 变换(消元法)而第7章用矩阵运算
从解联立方程的视点 • 视点1:着重研究解x,即研究线性方程组的解法。 中学里做的就是这样,前面介绍的用MATLAB矩 阵除法的解也是如此。 要点:矩阵的每一行代表一个方程,m行代表m 个线性联立方程。 n列代表n个变量。如果m是独 立方程数,根据mn确定方程是’欠 定’、’适定’还是’超定’。对这三种情况都 会求解了,研究就完成了。 必须剔除非独立方程。行阶梯形式、行列式和秩的 概念很大程度上为此目的而建立。 本书6,7两章对应于本视点,区别是第6章用行阶梯 变换(消元法)而第7章用矩阵运算
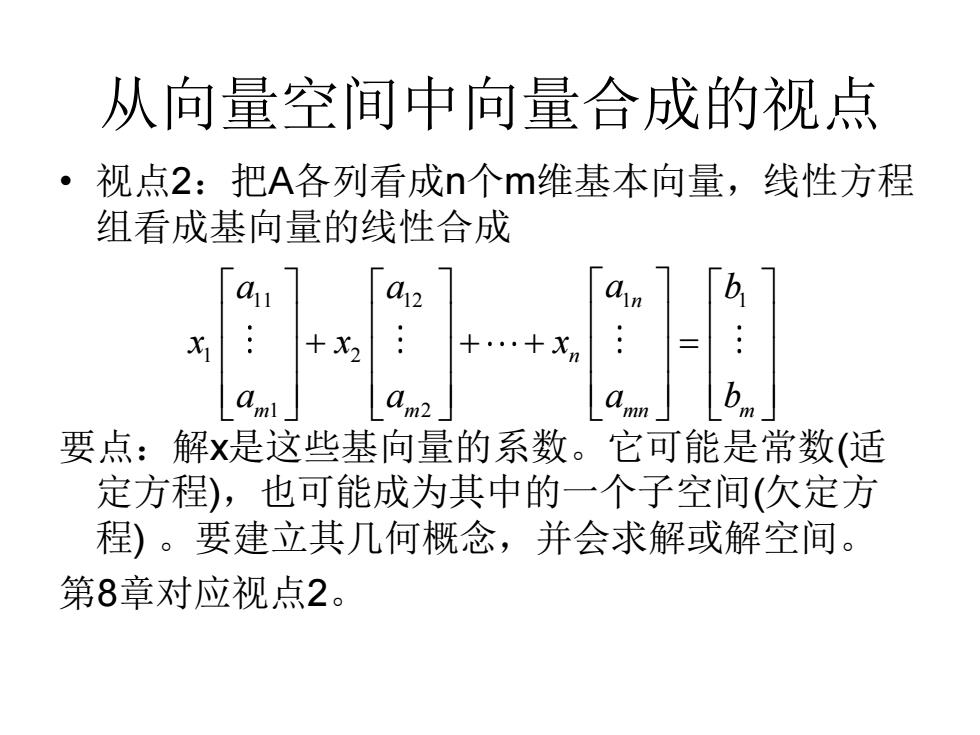
从向量空间中向量合成的视点 。 视点2:把A各列看成n个m维基本向量,线性方程 组看成基向量的线性合成 12 X +X2 +…+Xm am am2 要点:解是这些基向量的系数。它可能是常数(适 定方程),也可能成为其中的一个子空间(欠定方 程)。要建立其几何概念,并会求解或解空间。 第8章对应视点2
从向量空间中向量合成的视点 • 视点2:把A各列看成n个m维基本向量,线性方程 组看成基向量的线性合成 要点:解x是这些基向量的系数。它可能是常数(适 定方程),也可能成为其中的一个子空间(欠定方 程) 。要建立其几何概念,并会求解或解空间。 第8章对应视点2。 11 12 1 1 1 2 1 2 n n m m mn m a a b a x x x a a a b + + + =
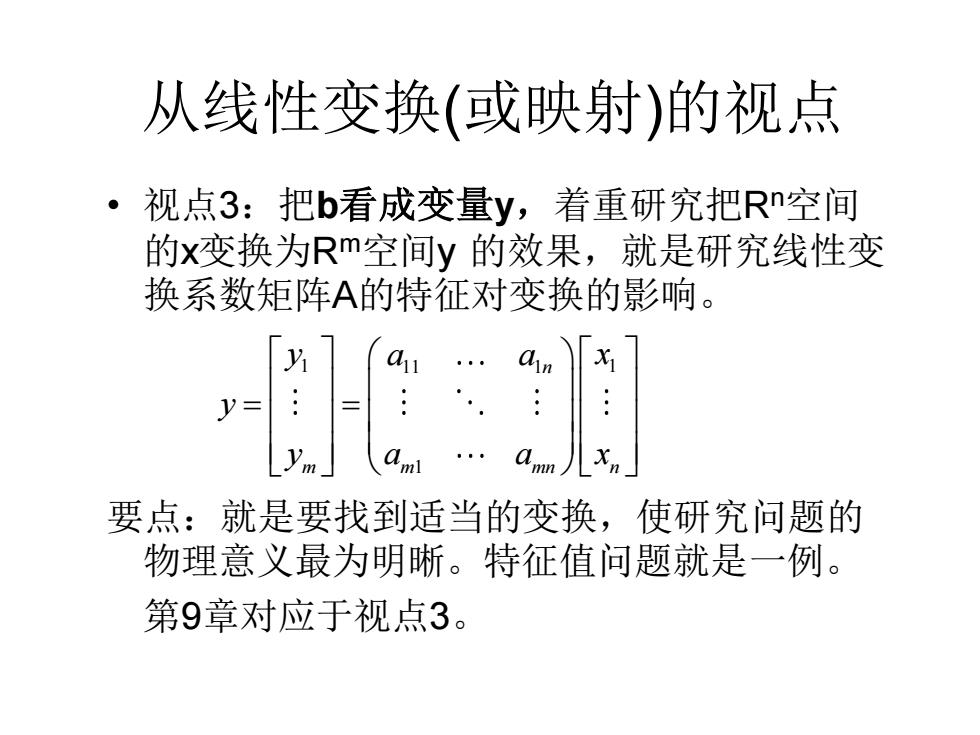
从线性变换(或映射)的视点 。 视点3:把b看成变量y,着重研究把Rn空间 的x变换为Rm空间y的效果,就是研究线性变 换系数矩阵A的特征对变换的影响。 y= 要点:就是要找到适当的变换,使研究问题的 物理意义最为明晰。特征值问题就是一例。 第9章对应于视点3
从线性变换(或映射)的视点 • 视点3:把b看成变量y,着重研究把Rn空间 的x变换为Rm空间y 的效果,就是研究线性变 换系数矩阵A的特征对变换的影响。 要点:就是要找到适当的变换,使研究问题的 物理意义最为明晰。特征值问题就是一例。 第9章对应于视点3。 1 1 11 1 1 n m m mn n y x a a y y a a x = =

学习本课的方法 在学习本书之前,对理论结果应已基本掌 握。 首先着重于对低阶概念的理解,要在二维 和三维空间内体会线性代数的定义。 。 结合相应的MATLAB程序,弄清低阶的算法, 然后再引伸到高阶方程中去,进一步搞清 其算法和程序应有的扩展。 对于应用问题,不必全看,可结合自已能 理解的问题先看
学习本课的方法 • 在学习本书之前,对理论结果应已基本掌 握。 • 首先着重于对低阶概念的理解,要在二维 和三维空间内体会线性代数的定义。 • 结合相应的MATLAB程序,弄清低阶的算法, 然后再引伸到高阶方程中去,进一步搞清 其算法和程序应有的扩展。 • 对于应用问题,不必全看,可结合自已能 理解的问题先看

5.3直线和平面的快速绘制程序 ·平面曲线的快速绘制程序ezplot(‘,[a,b]) 一引号中函数可以只有一个自变量,代表显函数 ·ezplot(f(x',[a,b]) ·系统将在a<x<b的范围内画出f=f() 一引号中的函数若有两个自变量,那就代表隐函 数,其典型格式为 ezplot('f(x,y)',[a,b]) ·系统将在a<x<b的范围内画出fx,y)=0。 -[a,b]的默认值为[-2π,2π]
5.3 直线和平面的快速绘制程序 • 平面曲线的快速绘制程序 ezplot(‘ ‘,[a,b]) – 引号中函数可以只有一个自变量,代表显函数 • ezplot(‘f(x)’, [a,b]) • 系统将在 a < x < b的范围内画出 f = f(x) – 引号中的函数若有两个自变量,那就代表隐函 数,其典型格式为 • ezplot(‘f(x,y)’, [a,b]) • 系统将在 a < x < b的范围内画出 f(x,y)=0。 – [a,b]的默认值为[-2π, 2π]

曲线快速绘制举例(例5.1) 。ezplot(x1+0.2*x23+1') -画出x,+0.2x+1=0在x=[-2T,-2T]的曲线 画多条曲线可按下列方法编程 ·S1='X1+0.2*X23+1' %方程1 ·S2=3*X1+2*X2+3 %方程2 ·ezplot(s1),nold on %画方程1,保持 ·ezplot(s2),grid on %画方程2,加网格 ·[x1,x2]=soVe(s1,s2) %解联立方程1,2
曲线快速绘制举例(例5.1) • ezplot(‘x1+0.2*x2^3+1’) – 画出 在x1=[-2π, -2π]的曲线 画多条曲线可按下列方法编程 • s1='x1+0.2*x2^3+1' % 方程1 • s2='3*x1+2*x2+3' % 方程2 • ezplot(s1),hold on % 画方程1,保持 • ezplot(s2),grid on % 画方程2,加网格 • [x1,x2]=solve(s1,s2) % 解联立方程1,2 3 1 2 x x + + = 0.2 1 0