
第五章 变换域中的离散时间系统
1 第五章 变换域中的离散时间系统

5.1z变换 ·傅氏变换有两个缺点,其一,在实际中 许多有用的信号,如μ(n)和n*u(n).等,它 们的离散傅利叶变换不存在。其二,系 统对初始条件的暂态响应,或由时变输 入引起的系统响应,都无法用离散傅利 叶变换方法来计算。 ·为了克服上述的两个缺点,要把离散傅 利叶变换方法进行推广,推广后的方法 称为z变换。 2
2 5.1 z变换 • 傅氏变换有两个缺点,其一,在实际中 许多有用的信号,如μ(n)和n* μ(n)...等,它 们的离散傅利叶变换不存在。其二,系 统对初始条件的暂态响应,或由时变输 入引起的系统响应,都无法用离散傅利 叶变换方法来计算。 • 为了克服上述的两个缺点,要把离散傅 利叶变换方法进行推广,推广后的方法 称为z变换

z变换的定义 定义:对于一个序列x(n),其双边z变换定义为: X(2)=ZIx(n】=∑x(n)z” n=-o0 其中z=pe0是复变量,其向径为p,幅角为p, 构成一个复平面,称为z平面。 序列xn)的单边z变换则定义为: X+(z):=Z+[x(n】=∑x(n)z” n=0 3
3 z变换的定义 定义:对于一个序列x(n),其双边z变换定义为: 其中 是复变量,其向径为ρ,幅角为φ, 构成一个复平面,称为z平面。 序列x(n)的单边z变换则定义为: . =− − = = n n X(z) : Z[x(n)]: x(n)z j z = e = + + − = = 0 ( ) : [ ( )]: ( ) n n X z Z x n x n z

z变换的定义 ·例如,对于序列x=1.5,0,5,2,-2,31 它的双边z变换是: X(z)=1.5z2+0.5z+2z0-2z1+3z2-z3 其单边z变换是: X+(z)=2z0-2z1+3z2-23 如果序数向量n只取正值,称为右序列,右序列 的z变换X(z)中只出现z的负次幂;当采样序数n 取负值时,X(z)中将出现z的正次幂。在工程中, 人们感兴趣的主要是右序列。 4
4 z变换的定义 • 例如,对于序列 它的双边z变换是: 其单边z变换是: 如果序数向量n只取正值,称为右序列,右序列 的z变换X(z)中只出现z的负次幂;当采样序数n 取负值时,X(z)中将出现z的正次幂。在工程中, 人们感兴趣的主要是右序列。 x = 1.5,0,5,2,−2,3,−1 2 0 1 2 3 ( ) 1.5 0.5 2 2 3 − − − X z = z + z + z − z + z − z 0 1 2 3 ( ) 2 2 3 + − − − X z = z − z + z − z

z变换的收敛域 z变换的收敛性 1.有限长序列:在除原点外的全z平面上收敛; 2。无限长右序列:在一个半径为r(称为收敛 半径)的圆外的全z平面上收敛; 3。无限长左序列:在一个半径为r(也称为收 敛半径)的圆内收敛; 4。双向无限序列:右序列和右序列收敛区的 (环形)公共区,也可能没有; 分别见下图中子图(a),(b),(c),(d)。 5
5 z变换的收敛域 z变换的收敛性 1.有限长序列:在除原点外的全z平面上收敛; 2。无限长右序列:在一个半径为r(称为收敛 半径)的圆外的全z平面上收敛; 3。无限长左序列:在一个半径为r(也称为收 敛半径)的圆内收敛; 4。双向无限序列:右序列和右序列收敛区的 (环形)公共区,也可能没有; 分别见下图中子图(a),(b),(c),(d)
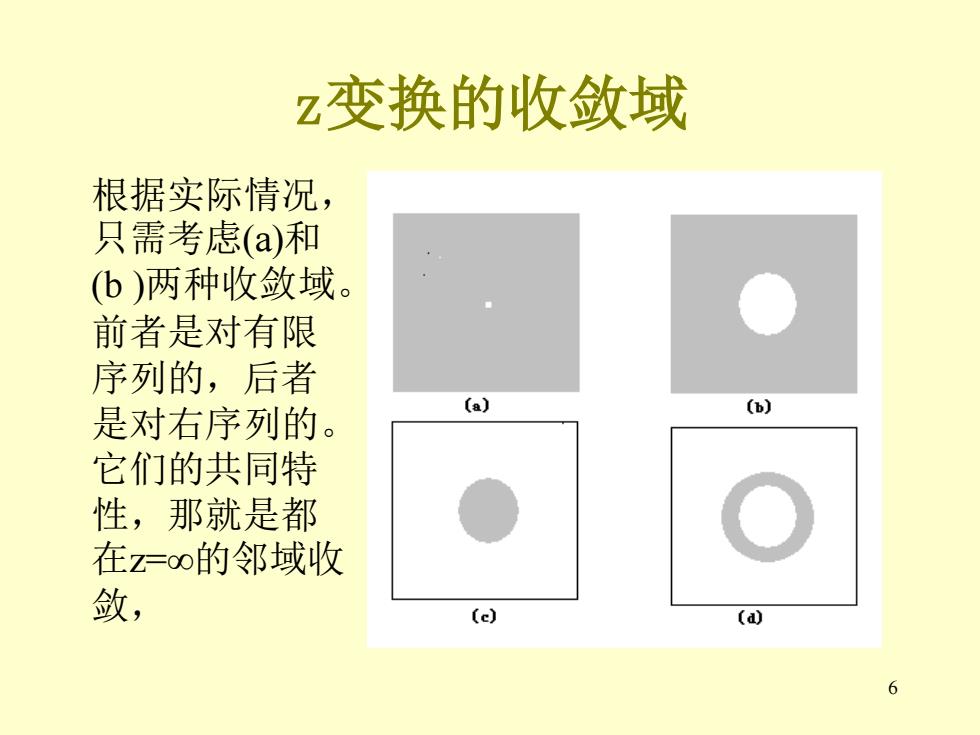
z变换的收敛域 根据实际情况, 只需考虑(a)和 (b)两种收敛域。 前者是对有限 序列的,后者 (a) 是对右序列的。 (b) 它们的共同特 性,那就是都 在z=oo的邻域收 敛, (e) (a 6
6 z变换的收敛域 根据实际情况, 只需考虑(a)和 (b )两种收敛域。 前者是对有限 序列的,后者 是对右序列的。 它们的共同特 性,那就是都 在z=∞的邻域收 敛

z反变换 单边或双边z变换的反变换定义为。 o=zrLe-=2gKekb 其中,积分路径是在复数平面中处于收敛 域中的一条围线。 在数字信号处理中,不需要用围线积分来 求z反变换。5.2节中,将专门讨论求z反 变换的其它方法。 7
7 z反变换 单边或双边z变换的反变换定义为。 其中,积分路径是在复数平面中处于收敛 域中的一条围线。 在数字信号处理中,不需要用围线积分来 求z反变换。5.2节中,将专门讨论求z反 变换的其它方法。 X z z dz j x n Z X z n C 1 1 ( ) 2 1 ( ) : [ ( )] − − = =

z反变换的非单值性 右序列: =65” n=0,12,… n<0 和左序列: [0 n≥0 x(n)= -1.5)m n<0 两个不同的序列具有相同的z变换 1.5-1z X(z)= 1-1.5-1z z-1.5 因此必须规定z变换的收敛域,本书限定研究在∞ 邻域收敛的右序列。故其反变换唯一。 8
8 z反变换的非单值性 右序列: 和左序列: 两个不同的序列具有相同的z变换 因此必须规定z变换的收敛域,本书限定研究在∞ 邻域收敛的右序列。故其反变换唯一。 = = 0 0 1.5 0,1,2, ( ) n n x n n − = − (1.5) 0 0 0 ( ) n n x n n 1 1.5 1.5 1.5 ( ) : 1 1 − = − = − − − z z z z X z

z变换的重要特性 ·z变换的特性与DTFT和DFT的特性有很多相似 之处,其证明都可以类比或从定义直接导出, 所以不再重复推证。这里着重讨论几个重要特 性的意义和应用。因为讨论都限于右序列,所 以也免除了对收敛域的说明。 ·1.线性特性: 设Z[g(n)]=G(z),Z[h(n)]=H(z),a,β为常数, 则 Za g(n)+B h(n)=a G(=)+B H(=) 9
9 z变换的重要特性 • z变换的特性与DTFT和DFT的特性有很多相似 之处,其证明都可以类比或从定义直接导出, 所以不再重复推证。这里着重讨论几个重要特 性的意义和应用。因为讨论都限于右序列,所 以也免除了对收敛域的说明。 • 1.线性特性: 设Z[g(n)]=G(z), Z[h(n)]=H(z), α,β为常数, 则 Z g(n) + h(n)= G(z) + H(z)

z变换的重要特性 ·2。样本的移位: Z[g(n-n小=zG(z) ·3。序列卷积: Z g(n)*h(n)=G().H(z) ·4。初值定理 mce)=8tms” =8(0) n=0 10
10 z变换的重要特性 • 2。样本的移位: • 3。序列卷积: • 4。初值定理 0 0 ( ) ( ) n Z g n n z G z − − = Z g n h n G z H z ( ) ( ) ( ) ( ) = lim ( ) ( ) (0) 0 G z g n z g z n n z = = → = − →