
数字信号处理教程 —MATLAB释义与实现 陈怀琛编著
1 数字信号处理教程 —MATLAB释义与实现 陈怀琛编著

第一章信号和信号处理 1.1信号的分类 1.2信号处理 1.3信号采样和复原的一个实例 1.4本书概貌的说明 2
2 第一章 信号和信号处理 1.1 信号的分类 1.2 信号处理 1.3 信号采样和复原的一个实例 1.4 本书概貌的说明

1.1信号的分类 ·按信号载体的物理特征,可分为电、磁、 光、机械、热、声音等; ·按信号中的自变量的数目分: -一维信号:如语言和音乐 -二维信号:如黑白照片或地形图, -三维信号:如黑白电视图象, (彩色图像或电视是三个因变量,自变量同上) 3
3 1.1 信号的分类 • 按信号载体的物理特征,可分为电、磁、 光、机械、热、声音等; • 按信号中的自变量的数目分: –一维信号:如语言和音乐 –二维信号:如黑白照片或地形图, –三维信号:如黑白电视图象, (彩色图像或电视是三个因变量,自变量同上)

信号的分类 ·按信号中自变量和因变量的取值特点分 ·连续时间(Continuous-Time一CT)信号: 自变量和因变量均连续取值,(自变量的连续 称为连续时间,因变量的连续称为模拟信号) ·离散时间(Discrete-Time一DT)信号: 自变量离散,因变量仍连续取值 ·数字信号(Digital Signal): 自变量和因变量均离散取值(因变量的离散称为数 字信号) 4
4 信号的分类 • 按信号中自变量和因变量的取值特点分 • 连续时间(Continuous-Time—CT)信号: 自变量和因变量均连续取值,(自变量的连续 称为连续时间,因变量的连续称为模拟信号) • 离散时间(Discrete-Time—DT)信号: 自变量离散,因变量仍连续取值 • 数字信号(Digital Signal): 自变量和因变量均离散取值(因变量的离散称为数 字信号)

信号的分类 ·信号量化的方法 -自变量的量化:等间隔采样,n工,n=0,1, ·T为采样周期,也即量化步长 -因变量x的量化: ·设量化步长为△x,则量化公式为 xq=△x·round(x/△x) ·对应的MATLAB语句(x为数组也适用) xq=round(x/deltax)*deltax; 其它取整函数有cei1,f1oor,fix等 5
5 信号的分类 • 信号量化的方法 – 自变量的量化:等间隔采样,t=nT, n=0,1,… • T为采样周期,也即量化步长 – 因变量x的量化: • 设量化步长为△x,则量化公式为 •对应的MATLAB语句(x为数组也适用) xq=round(x/deltax)*deltax; 其它取整函数有ceil,floor,fix等 xq = x round(x / x)

信号的分类 ·由对模拟信号采样而产生离散信号x) x(n))=xa(i=nT n=0,1,2…,W-1 ·量化后信号xq的误差 一绝对误差 e-xq-x -相对误差rerror=(xq-)./abs(x) -对大的数,量化造成的相对误差小;而对小的数, 量化造成的相对误差大。 6
6 • 由对模拟信号采样而产生离散信号x(n) • 量化后信号xq的误差 – 绝对误差 e=xq-x – 相对误差 rerror=(xq-x)./abs(x) –对大的数,量化造成的相对误差小;而对小的数, 量化造成的相对误差大。 信号的分类 ( ) = ( ) , = 0,1,2, , −1 = x n x t n N a t n T

信号分类的例题 。例1.1.1设连续信号为 xa(t)=Vt+cost 0≤t≤tf=6 -其中f为终点时刻。若采样周期为0.5秒,求采样后 的离散时间信号 -MATLAB程序hc111 7
7 信号分类的例题 • 例1.1.1 设连续信号为 –其中tf为终点时刻。若采样周期为0.5秒,求采样后 的离散时间信号 – MATLAB程序hc111 xa (t) = t + cost 0 t t f = 6

例1.1.1的MATLAB:程序hc111 此程序分别描述了连续信号、离散信号和数字信号 dt=0.001;tf=6;t=0:dt:tf;号建立自变量向量 xa=sqrt(t)+cos(t);原始的连续时间信号xa(t)》 T=0.5;n=0:tf/T;号建立离散自变量向量 x=sqrt(n*T)+cos(n*T);号离散时间信号x(n) deltax=0.5; 号deltax为x的量化步长 xq=round(x/deltax)*deltax;号量化的数字信号xg ·以下为绘图语句 8
8 例1.1.1的MATLAB程序hc111 此程序分别描述了连续信号、离散信号和数字信号 dt=0.001; tf=6; t=0:dt:tf;% 建立自变量向量 xa=sqrt(t)+cos(t); % 原始的连续时间信号xa(t) T=0.5;n=0:tf/T;% 建立离散自变量向量 x=sqrt(n*T)+cos(n*T); % 离散时间信号x(n) deltax=0.5; % deltax为x的量化步长 xq=round(x/deltax)* deltax;% 量化的数字信号xq • 以下为绘图语句
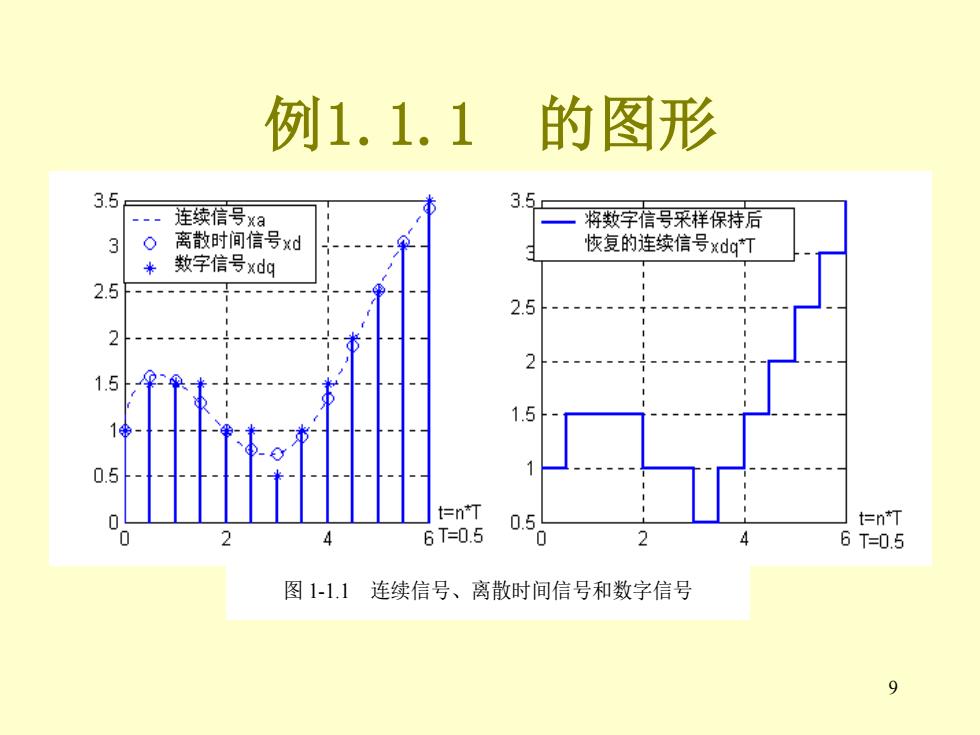
例1.1.1 的图形 3.5 3.5 连续信号xa 将数字信号采样保持后 3 离散时间信号xd 恢复的连续信号xdgT 数字信号xdg 2.5 2.5 2 1.5 1.5 t仁nT 0.5 t仁n*T 6T=0.5 0 6T=0.5 图1-1.1连续信号、离散时间信号和数字信号 9
9 例1.1.1 的图形 图 1-1.1 连续信号、离散时间信号和数字信号

信号的分类 ·按照信号的来源来分 -心电(ElectroCardioGraphy--ECG)信号: -脑电图(ElectroEncephaloGram-一EEG)信号 -地震信号:它由岩石的自然运动、或人为的地下爆 炸等产生。 -发动机振动信号: -语言信号: -音乐信号: -统计数据: 等等 10
10 • 按照信号的来源来分 –心电(ElectroCardioGraphy—ECG)信号: –脑电图(ElectroEncephaloGram—EEG)信号 –地震信号:它由岩石的自然运动、或人为的地下爆 炸等产生。 –发动机振动信号: –语言信号: –音乐信号: –统计数据: 等等 信号的分类