
附录A MATLAB 矩阵代数和作图初步
附录A MATLAB 矩阵代数和作图初步

MATLAB简介 ·MATLAB是“矩阵实验室”(MATrix LABoratoy)的缩写, 它是一种以矩阵运算为基础的交互式程序语言,专 门针对科学、工程计算及绘图的需求。与其他计算 机语言相比,其特点是简活和智能化。适应料技专 是全装·义桂容发实大 它用解释方式工作,键入程序后立即得出结果:,它 的自学也千分方便,通过它的演示(demo)和求助 (help)命令,人们可以方便地在线学习各种函数的用 法及其内涵。 MATLAB语言与高等数学的关系十分密切。作者认为 最好是尽早入门,但入门起码要有矩阵的基础,所 以和线性代数同步学习是最佳的选择
MATLAB简介 • MATLAB是“矩阵实验室”(MATrix LABoratoy)的缩写, 它是一种以矩阵运算为基础的交互式程序语言,专 门针对科学、工程计算及绘图的需求。与其他计算 机语言相比,其特点是简洁和智能化。适应科技专 业人员的思维方式和书写习惯;它还包含了大量的 科学计算函数库,使得编程和调试效率大大提高; 它用解释方式工作,键入程序后立即得出结果;它 的自学也十分方便,通过它的演示(demo)和求助 (help)命令,人们可以方便地在线学习各种函数的用 法及其内涵。 • MATLAB语言与高等数学的关系十分密切。作者认为 最好是尽早入门,但入门起码要有矩阵的基础,所 以和线性代数同步学习是最佳的选择

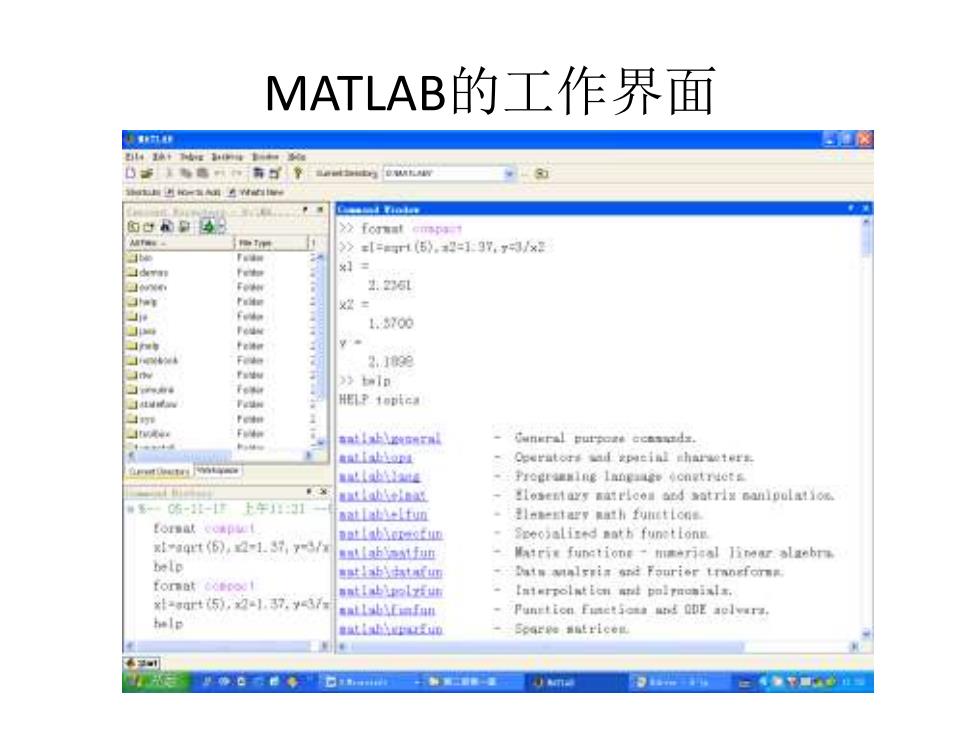
1.MATLAB的工作界面 在Vindows.桌面上,双击MATLAB的图标,就可进入 MATLAB的工作环境。如图A-1所示。它的右方是键 ◇建含養有数字复盟区整称阁部含示 了该命令产生的计算结果。数据的默认显示格式为 五位有效数字,可角format命令改变输出格式 help是获取帮助的命令,在它之后应该跟二个主题 词,,例如nelp format,系统就会对format的用法提 供说明。图A-1中在help之后没有主题,它只列出了 在此系统中所有的MATLAB函数库名。 键入figure命令可以生成图形窗,以显示MATLAB程 序产生的图形。另一个常用到的视窗是“文本编辑 ”,只要点击命令窗上部最左边的两个菜单图标 就可打开,可用它来编辑和修改程序文件
1.MATLAB的工作界面 • 在Windows桌面上,双击MATLAB的图标,就可进入 MATLAB的工作环境。如图A-1所示。它的右方是键 入命令和获得数字计算结果的区域,称为命令窗。 >>是它的提示符,在>>之后键入命令,图中已显示 了该命令产生的计算结果。数据的默认显示格式为 五位有效数字,可用format命令改变输出格式。 help是获取帮助的命令,在它之后应该跟一个主题 词,例如help format,系统就会对format的用法提 供说明。图A-1中在help之后没有主题,它只列出了 在此系统中所有的MATLAB函数库名。 • 键入figure命令可以生成图形窗,以显示MATLAB程 序产生的图形。另一个常用到的视窗是“文本编辑 窗”,只要点击命令窗上部最左边的两个菜单图标 就可打开,可用它来编辑和修改程序文件
MATLAB的工作界面 图 0子主与路新尊 Csml Tiote >2fc灯tGg >l=e1(50,2=137,y-3/×2 f短 ×1= ECA 2.2951 ×程= f标 Fenbne : 1.8700 Ye e 2,1839 白 fa地 tln 域d Peshnd HE1?topica ye Pettet a士l止约高r neral putpore cca时d aatiakiont Cperators tad zpacial sharaeters. ylako ptiabkoinav lesertayr aatrleos and aatrix nanlpulatioo -C6-11-1F上年j131 et Lateltyn lenerta驶math functicn nnth以rofw Speojalized aath funetionn -aqt(6,21.37,7/ abs1fu边 atris funetione一mwri和sl1 inear alaeb belp 上ah由tf四 Datu Malsria and Fourier traneforns. s山z线 -【aterpolat ion an palrnoaial x0rt50,2-1.37,¥37 satlab\Cimfan -Punrticn Fuetiona an ODE aclvars help atLabieoEu Eparge sntricen 海。, ow。=4童e■
MATLAB的工作界面

2.矩阵及其赋值 ● 1)标识符与数 ● 标识符是标识变量名、常量名、,函数名和文件名的字符串的总 称。在MATLAB中,变量和常量的标识符最长为19个 符,.函数 和文件名则通常不超过8个字符。这些字符包括全部的英文字母 (大小写共52个、,阿拉伯数字和下划线等符号,但其中第个 字符必须是英文字母。MATLAB对大小写敏感(Case Sensitive), 即它把A和a看做两个不同的字符。 。 MATLAB内部只有一种数据格式,那就是双精度(即64位二进制), 对应于十进制16位有效数和士308次幂。MATLAB做运算和存储 时都用双精度格式,这对绝大多数工程计算是足够的。虽然它 的数据存储格式只有二种,但显示格式有多种,format short是 默认条件,显示5位十进制有效数位:用format long命令后,显 示16位有效数位;用format rat命令后显示有理数分数;format compact则使显示结果紧凑,去掉空行。 MATLAB的每一个元素都可以是复数,实数是复数的特例。复数 的虚数部分用i或j表示。这是在MATLAB启动时就在内部设定的
2.矩阵及其赋值 • 1) 标识符与数 • 标识符是标识变量名、常量名、函数名和文件名的字符串的总 称。在MATLAB中,变量和常量的标识符最长为19个字符,函数 和文件名则通常不超过8个字符。这些字符包括全部的英文字母 (大小写共52个)、阿拉伯数字和下划线等符号,但其中第一个 字符必须是英文字母。MATLAB对大小写敏感(Case Sensitive), 即它把A和a看做两个不同的字符。 • MATLAB内部只有一种数据格式,那就是双精度(即64位二进制), 对应于十进制16位有效数和±308次幂。MATLAB做运算和存储 时都用双精度格式,这对绝大多数工程计算是足够的。虽然它 的数据存储格式只有一种,但显示格式有多种,format short是 默认条件,显示5位十进制有效数位;用format long命令后,显 示16位有效数位;用format rat命令后显示有理数分数;format compact则使显示结果紧凑,去掉空行。 • MATLAB的每一个元素都可以是复数,实数是复数的特例。复数 的虚数部分用i或j表示。这是在MATLAB启动时就在内部设定的

2。矩阵及其元素的赋值 ·赋值就是把数赋予代表变量的标识符。MATLAB中的变量或常量 都代表矩阵,标量应看做1×1阶的矩阵。矩阵的值放在方括号 中,同一行中各元素之间以逗号或空格分开,不同的行则以分 号隔开,语句的结尾可用回车符或逗 号,此时会立即显示运算 结果。如果不希望显示结果,就以分号结尾。此时运算仍然执 行,只是不显示。例如输入语句 ·a=[123;456;789] 则显示结果为 a=123 456 789 。 元素也可以用表达式代替,如输入: X=[-1.3,sqrt(3),(1+2+3)/5*4] 。 结果为 ● x=-1.3000 1.7321 4.8000
2。 矩阵及其元素的赋值 • 赋值就是把数赋予代表变量的标识符。MATLAB中的变量或常量 都代表矩阵,标量应看做1 1阶的矩阵。矩阵的值放在方括号 中,同一行中各元素之间以逗号或空格分开,不同的行则以分 号隔开,语句的结尾可用回车符或逗号,此时会立即显示运算 结果。如果不希望显示结果,就以分号结尾。此时运算仍然执 行,只是不显示。例如输入语句 • a=[1 2 3;4 5 6;7 8 9] • 则显示结果为 • a= 1 2 3 • 4 5 6 • 7 8 9 • 元素也可以用表达式代替,如输入: • x=[-1.3,sqrt(3),(1+2+3)/5*4] • 结果为 • x=-1.3000 1.7321 4.8000

变量下标的使用 变量中的元素序号用“()”中的数字(也称为下标) 来注明,一维矩阵(也称数组或向量)中的元素用 个下标表示,二维的矩阵可有行号和列号两个下标 数,以逗号分开。用户可以单独给元素赋值,如果 赋值元素的下标超出了原来矩阵的大小,、则矩阵的 行列会自动扩展。如在上述x的赋值语句之后键入: · x(5)=abs(x(1) ·得: ·×=-1.30001.7321 4.8000 01.3000 ·给全行赋值,可用冒号。例如,给a的第5行赋值。 可键入: ·a(4,3)=6.5;a(5,:)=[5,4,3]
变量下标的使用 • 变量中的元素序号用“( )”中的数字(也称为下标) 来注明,一维矩阵(也称数组或向量)中的元素用一 个下标表示,二维的矩阵可有行号和列号两个下标 数,以逗号分开。用户可以单独给元素赋值,如果 赋值元素的下标超出了原来矩阵的大小,则矩阵的 行列会自动扩展。如在上述x的赋值语句之后键入: • x(5)=abs(x(1)) • 得: • x =-1.3000 1.7321 4.8000 0 1.3000 • 给全行赋值,可用冒号。例如,给a的第5行赋值。 可键入: • a(4,3)=6.5; a(5, :)=[5,4,3]

矩阵赋值(续) 得:a=1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 ● 0 0 6.5000 ● 5.0000 4.0000 3.0000 可见,跳空的元素x(4),a(4,1),a(4,2)被自动赋值为0。这种 自动扩展维数的功能只适用于赋值语句。在其他语句中若出现 超维调用的情况,、系统将瓮出出错提示。一个矩阵的所有元素 都要用同样的格式显示,因为出现了a(4,3)=6.5,所以a的所有 元素都有了小数点。 把a的第二,,四行及第一,三列交点上的元素取出,构成一个新 矩阵b。可键入: b=a([2,4],[1,3]) ·得:b= 4.0000 6.0000 0 6.5000
矩阵赋值(续) 得:a =1.0000 2.0000 3.0000 • 4.0000 5.0000 6.0000 • 7.0000 8.0000 9.0000 • 0 0 6.5000 • 5.0000 4.0000 3.0000 • 可见,跳空的元素x(4),a(4,1),a(4,2)被自动赋值为0。这种 自动扩展维数的功能只适用于赋值语句。在其他语句中若出现 超维调用的情况,系统将给出出错提示。一个矩阵的所有元素 都要用同样的格式显示,因为出现了a(4,3)=6.5,所以a的所有 元素都有了小数点。 • 把a的第二,四行及第一,三列交点上的元素取出,构成一个新 矩阵b。可键入: b = a([2,4],[1,3]) • 得:b = 4.0000 6.0000 0 6.5000

空矩阵和矩阵元素的删除 ·要删除a中的第二、四、五行,可利用空矩阵([)的概念。 键入: a([2,4,5],:)=[] ·得:a= 123 789 洼意,“窑阵”是指婆有云春的矩阵兵对凭但金阵赋以 值门,就是使它的元素都消尖獐。这完全不茼宇“零矩库分 后者是云素存在,一尽是基数值为零而己。可以看出,空矩阵是 佞矩库减缩时宋可缺少的瓣卷。 a'为矩阵a的共轭转置命令。若a是实数矩阵,则它就是矩阵a的 转置。此处键入a',得到: ans 17 28 39
空矩阵和矩阵元素的删除 • 要删除a中的第二、四、五行,可利用空矩阵([ ])的概念。 • 键入: a([2,4,5],:)=[ ] • 得:a = 1 2 3 7 8 9 • 注意,“空矩阵”是指没有元素的矩阵。对任何一个矩阵赋以 值[ ],就是使它的元素都消失掉。这完全不同于“零矩阵”, 后者是元素存在,只是其数值为零而已。可以看出,空矩阵是 使矩阵减缩时不可缺少的概念。 • a'为矩阵a的共轭转置命令。若a是实数矩阵,则它就是矩阵a的 转置。此处键入a',得到: ans = 1 7 2 8 3 9
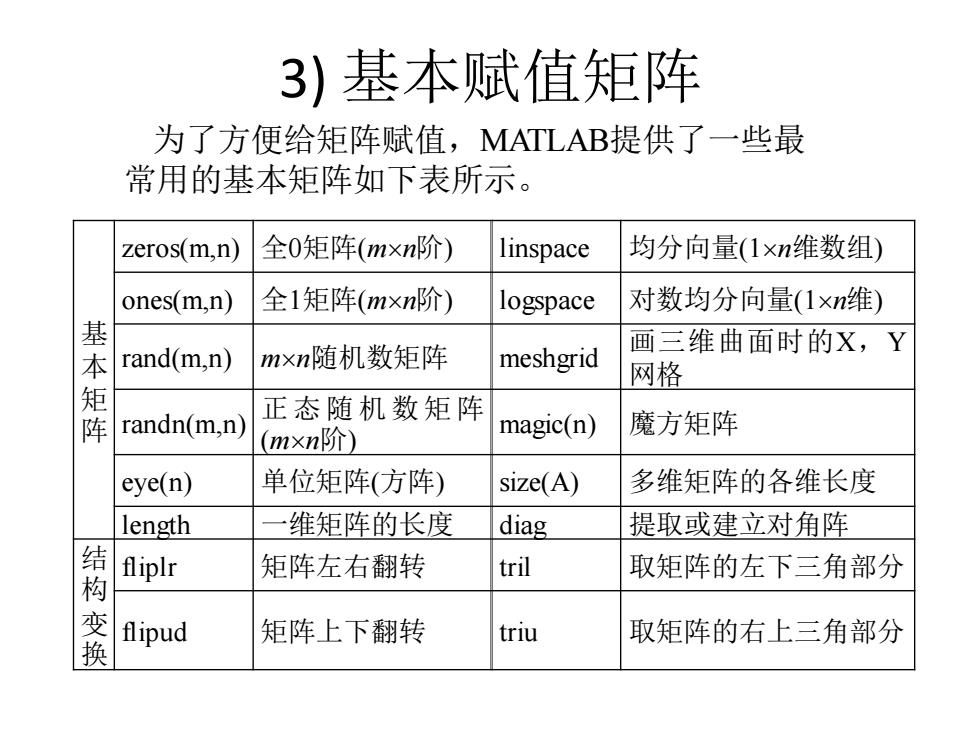
3)基本赋值矩阵 为了方便给矩阵赋值,MATLAB提供了一些最 常用的基本矩阵如下表所示。 zeros(m,n) 全0矩阵(mxn阶) linspace 均分向量(1xn维数组) ones(m,n) 全1矩阵(mxn阶) logspace 对数均分向量(1×n维) 本 rand(m,n) mxn随机数矩阵 meshgrid 画三维曲面时的X,Y 网格 正态随机数矩阵 阵 randn(m,n) (mxn阶) magic(n) 魔方矩阵 eye(n) 单位矩阵(方阵) size(A) 多维矩阵的各维长度 length 维矩阵的长度 diag 提取或建立对角阵 结 fliplr 矩阵左右翻转 tril 取矩阵的左下三角部分 flipud 矩阵上下翻转 triu 取矩阵的右上三角部分 换
3) 基本赋值矩阵 基 本 矩 阵 zeros(m,n) 全0矩阵(mn阶) linspace 均分向量(1n维数组) ones(m,n) 全1矩阵(mn阶) logspace 对数均分向量(1n维) rand(m,n) mn随机数矩阵 meshgrid 画三维曲面时的X,Y 网格 randn(m,n) 正态随机数矩阵 (mn阶) magic(n) 魔方矩阵 eye(n) 单位矩阵(方阵) size(A) 多维矩阵的各维长度 length 一维矩阵的长度 diag 提取或建立对角阵 结 构 变 换 fliplr 矩阵左右翻转 tril 取矩阵的左下三角部分 flipud 矩阵上下翻转 triu 取矩阵的右上三角部分 为了方便给矩阵赋值,MATLAB提供了一些最 常用的基本矩阵如下表所示