
论非数学类线性代数的内容改革 一如何用最浅显的理论解决更广泛的问题 西安电子科技大学陈怀琛hchchen1934vip.163.com 摘要:为了弄清线性代数中哪些理论是非数学类(下简称工科)学生必学的,采用了逆向思考的方 法,把后续课和工程中遇到的问题加以归纳,找到其最低限度需要的理论.。凡是后续课需要的,讲透加 强:凡是找不到直接需求的,即子省略;凡是能我到简明证法的,均予采纳.根据工科学生的特点,尽 量从具体到抽象,加强形象救学在理论证明中的作用。经过多年尝试,提出一些原则,并写出了教材以。 一、工科大学为什么要开线性代数课? 1960年前后,线性代数进入美国大学数学系本科教学计划叫,以后修这门课的非数学系等 生却成了主流:三十年前中国的工科是没有线性代数课的,80年代起增设这门课。线性代数 为什么在近几十年如此风靡呢?不是它在理论上有新突破,而是在应用上的创新。1973年的 诺贝尔经济奖发给了Leontiff教授,因为他1949年首创用计算机解了54阶线性方程组:80 年代初,线性代数软件包LINPACK开发成功, 这样人们不需要精通矩阵求解的数学细节,就 可以解决大型复杂的线性代数命题,MATLAB也是用此软件包作为后台支撑的。线性代数不 再是少数理论尖子才能学会的秘笈,而成为非数学专业大学生都能掌握的计算工具。 现代社会对工科数学提出了更高的要求。钱学森先生在1989年写道:“今后对一个问题求 解可以全部让电子计算机去干,不需要人去一点一点尊。而直到今天,工科理科大学一二年级 的数学课是构筑在人自己去算这一要求上的。…所以理工科的数学课必须改革,数学课不是 为了学生学会自己去求解,而是为了学生学会让电子计算机去求解,学会理解电子计算机给出 的答案”。线性代数是数值计算的基础,不但该率先使用计算机、而且该由它推动其他数 学和工程问题的计算机化。 线性代数的重要性主要体现在它把愈来愈多的新领域与计算机联系起来,Leontiff获经济 奖说明,想用计算机解决问题就得学线性代数。这种“需求牵引”对非数学专业而言,体现在 用计算机求解高阶复杂的矩阵模型, 不是去手工推证课程内部的微观数学公式。它与原数学系 的指导思想相差很大,在实施中师生都提出了改革要求。 实践多年后,美国在1990年提出了线性代数作为公共课的五条改革建议:(①)线性代数课 程要面向应用,满足非数学专业的需要:(的它应该是面向矩阵的(不是面向向量空间):(而) 它应该适应学生的水平和需要:(v)它应该利用最新的计算技术:(W)抽象内容应另设后续课程 来讲。这五条建议鲜明地指出了非数学系的线性代数与原有课程的重大区别。 “面向应用,满足非数学专业的需要”如何体现? 要做到这一点,必须深入到非数学专业的实我中去,而用计算机解矩阵方程组是问题的核 心。作者从十多门后续工程与管理课程中找到了两百多个应用例题,归纳它们的共同需求。大 体情况是:(1)最多的是解高阶方程组:阶次为515,工程中可高至数千。类型则适定的最 多,超定的其次,欠定的极少见:(2)向量相关性:大部分题目涉及空间几何形状和运动, 维为主:高维问题极少,而且通常都看做解方程,用行阶梯变换来解:(3)线性变换:大
论非数学类线性代数的内容改革 ——如何用最浅显的理论解决更广泛的问题 西安电子科技大学 陈怀琛 hchchen1934@vip.163.com 摘要:为了弄清线性代数中哪些理论是非数学类(下简称工科)学生必学的,采用了逆向思考的方 法,把后续课和工程中遇到的问题加以归纳,找到其最低限度需要的理论。凡是后续课需要的,讲透加 强;凡是找不到直接需求的,即予省略;凡是能找到简明证法的,均予采纳。根据工科学生的特点,尽 量从具体到抽象,加强形象教学在理论证明中的作用。经过多年尝试,提出一些原则,并写出了教材[2]。 一、工科大学为什么要开线性代数课? 1960 年前后,线性代数进入美国大学数学系本科教学计划[1],以后修这门课的非数学系学 生却成了主流;三十年前中国的工科是没有线性代数课的,80 年代起增设这门课。线性代数 为什么在近几十年如此风靡呢?不是它在理论上有新突破,而是在应用上的创新。1973 年的 诺贝尔经济奖发给了 Leontiff 教授,因为他 1949 年首创用计算机解了 54 阶线性方程组;80 年代初,线性代数软件包 LINPACK 开发成功。这样人们不需要精通矩阵求解的数学细节,就 可以解决大型复杂的线性代数命题,MATLAB 也是用此软件包作为后台支撑的。线性代数不 再是少数理论尖子才能学会的秘笈,而成为非数学专业大学生都能掌握的计算工具。 现代社会对工科数学提出了更高的要求。钱学森先生在 1989 年写道:“今后对一个问题求 解可以全部让电子计算机去干,不需要人去一点一点算。而直到今天,工科理科大学一二年级 的数学课是构筑在人自己去算这一要求上的。… 所以理工科的数学课必须改革,数学课不是 为了学生学会自己去求解,而是为了学生学会让电子计算机去求解,学会理解电子计算机给出 的答案…”。[4]线性代数是数值计算的基础,不但该率先使用计算机、而且该由它推动其他数 学和工程问题的计算机化。 线性代数的重要性主要体现在它把愈来愈多的新领域与计算机联系起来,Leontiff 获经济 奖说明,想用计算机解决问题就得学线性代数。这种“需求牵引”对非数学专业而言,体现在 用计算机求解高阶复杂的矩阵模型,不是去手工推证课程内部的微观数学公式。它与原数学系 的指导思想相差很大,在实施中师生都提出了改革要求。 实践多年后,美国在 1990 年提出了线性代数作为公共课的五条改革建议:(i)线性代数课 程要面向应用,满足非数学专业的需要;(ii)它应该是面向矩阵的(不是面向向量空间);(iii) 它应该适应学生的水平和需要;(iv)它应该利用最新的计算技术;(v)抽象内容应另设后续课程 来讲。这五条建议鲜明地指出了非数学系的线性代数与原有课程的重大区别。 二、“面向应用,满足非数学专业的需要”如何体现? 要做到这一点,必须深入到非数学专业的实践中去,而用计算机解矩阵方程组是问题的核 心。作者从十多门后续工程与管理课程中找到了两百多个应用例题,归纳它们的共同需求。大 体情况是:(1)最多的是解高阶方程组:阶次为 5~15,工程中可高至数千。类型则适定的最 多,超定的其次,欠定的极少见;(2)向量相关性:大部分题目涉及空间几何形状和运动, 三维为主;高维问题极少,而且通常都看做解方程,用行阶梯变换来解;(3)线性变换:大
量的应用问题属于欧几里得空间的坐标变换。把同类问题适当合并后,在本文末的附录中列举 了教材中近50个应用实例,给出了它们的阶数及特性。教材改革的理论选材,就是围绕这 些题目的需要组织起来的。 把高斯消元法解线性方程组作为全书的理论主线,把行列式也纳入这根主线上。尽 量去除不必要的紫 ,使理论单 化 (2)为了与计算机结合,要使学生建立计算复杂度和计算精度的概念,引入的方法和概 念都要把工程和计算可实现性摆在重要位置: (3)根据大一学生的水平,若重建立三维空间概念,不要求N难向量空间: 4进透适定和超定方程的MATLAB解法,弱化欠定方程的解,不讲基础解及解空间。 5)特征方程和特征根、 次型都只以二阶为主,但兼顾复数根, 这样组织的内容,与原有的数学系的线性代数就有了很大的不同,特别表现在以下方面。 三、行列式的定义和性质的讲法改革 我们发现,在所有的应用命题中,除了硬凑的求面积体积的题用到三阶行列式外,没有 个问顾直正要算三阶以上行列式的,花了很名学时进的各种行列式理论和方法意然没用处。原 因何在?这是因为用消元法解方程时,已经用主元都不为零判定了解的存在和唯一,不知不觉 中已用了主元连乘定义下行列式:不必另起炉灶,让学生 去学其他两种紫 货的高阶行列式定义 也用不到克拉默法则。主元连乘法是高斯消元的自然延伸,不引进新概念新名词,并可很容易 地证明行列式的各种有用的性质,也是软件编程的依据。 对于工程人才,数学定义和方法的可实现性是必须关注的问题。数值计算中通常用所需的 乘法次数来标志计算的复杂度,下表给出了行列式三种定义方法在不同阶数下的计算量比较 表3-1行列式日 种定义方法所需 阶数n 2345 10 25 1.悬式法(不含正负号计算)(-)n: 21272 480 326592003.72*1026 2.代数余子式法≈2 2940205 72576003.10*10°25 3。对角主元连乘法3 4132445342 5233 拿1,3两种方法所需的乘法次数加以比较,可以看出,只有=2时,用显式法求行列式才 比消元法方便。当n=10时,用显式法算的计算量为三千万次,主元连乘法才342次。n更大 时,两种老定义的运算量不仅超越了人们竿算可能性,也超越了计算机的能力。这种现象称为 se of Di e ality)”。在新定义下,不但计算量大 那些“逆疗 数 代数余子式、随伴矩阵 、行列式按行展开 等等只能给爱数学的人练练推导,根本 有实用价值。非数学系避开了这些“拦路虎”,可大大压缩篇幅,降低难度,何乐而不为呢。 不讲这些概念水平就低吗?其实这才是有水平:高屋建瓴,看透了传统定义的致命痼疾, 让后人别白费时间。经典的行列式定义出现最早,最繁琐,用绕它的公式也多,但只能推导不 能算:高斯消元法可直接得出行列式的主元连乘公式,计算很简单,有人就把简化说成水平低 r用 琐的 老定义加 推导来绕 ,非要繁才算高水 。好在到 了计算机时代,编程中自然会扬弃一切无用的中间环节。所以MATLAB中就没有这些繁琐过 时的术语及其子程序。当前全世界有几百万教学、科研和工程用户都在靠它解大规模、高难度 的线性代数问题,说明从应用出发,确实不需要这些概念。美国T的教材也不细讲这 术语,只通过 阶陈简单介绍了一下 好比,定义党手 工岩,要一尺一尺地爬。高斯法找到了筑台阶的办法,可以 级一级地走:计算机相当于发明缆车,可以一步到顶。根据非数学专业学生的基础和面临的实 际问题,该教什么是不言自明的。让少数数学系的学生练两天攀岩也许还有点道理,让千百万 非数学系的学生都去学攀岩,不坐缆车,实在讲不过去。 四、向量空间要讲透三维,减缩N维
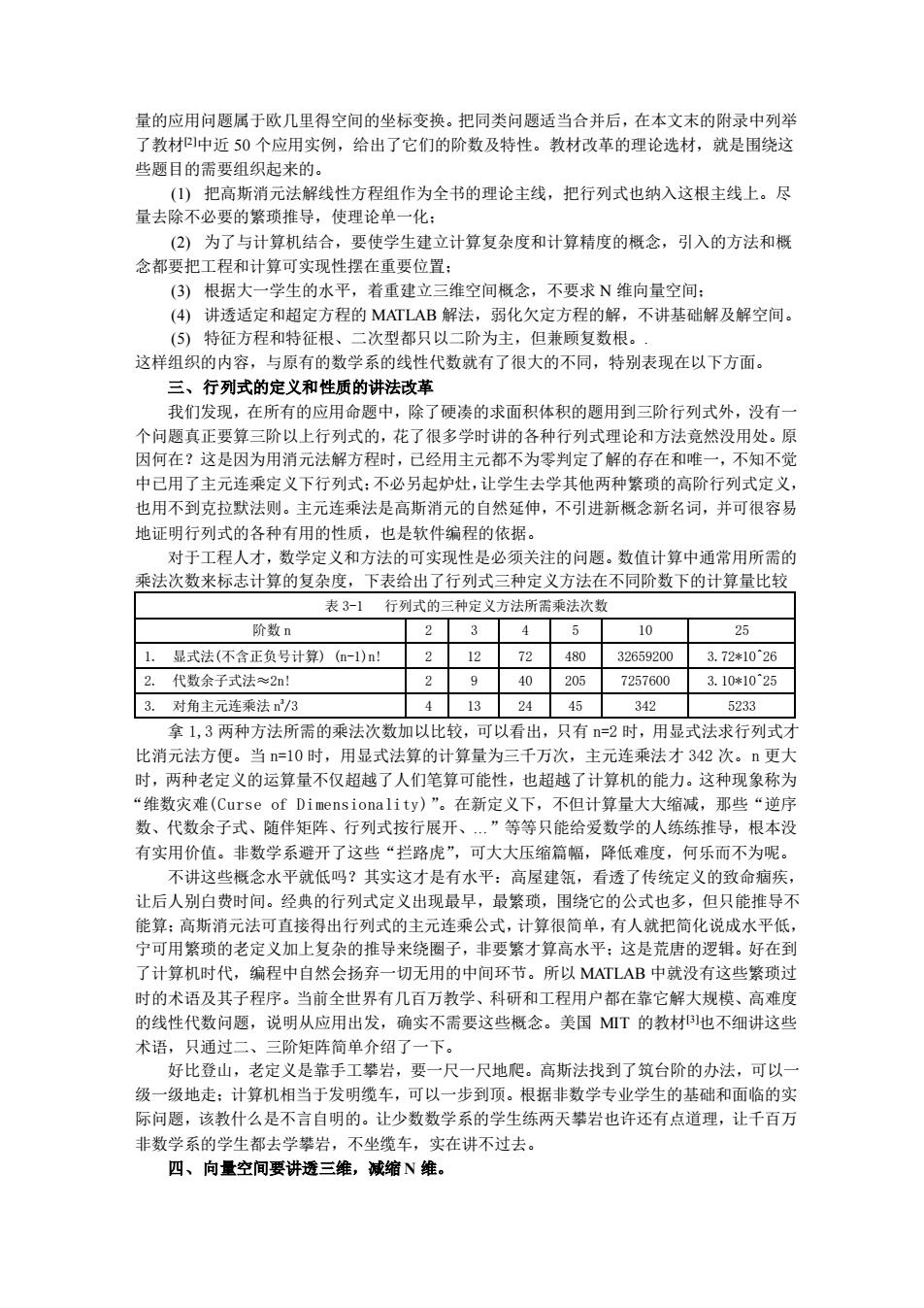
量的应用问题属于欧几里得空间的坐标变换。把同类问题适当合并后,在本文末的附录中列举 了教材[2]中近 50 个应用实例,给出了它们的阶数及特性。教材改革的理论选材,就是围绕这 些题目的需要组织起来的。 (1) 把高斯消元法解线性方程组作为全书的理论主线,把行列式也纳入这根主线上。尽 量去除不必要的繁琐推导,使理论单一化; (2) 为了与计算机结合,要使学生建立计算复杂度和计算精度的概念,引入的方法和概 念都要把工程和计算可实现性摆在重要位置; (3) 根据大一学生的水平,着重建立三维空间概念,不要求 N 维向量空间; (4) 讲透适定和超定方程的 MATLAB 解法,弱化欠定方程的解,不讲基础解及解空间。 (5) 特征方程和特征根、二次型都只以二阶为主,但兼顾复数根。. 这样组织的内容,与原有的数学系的线性代数就有了很大的不同,特别表现在以下方面。 三、行列式的定义和性质的讲法改革 我们发现,在所有的应用命题中,除了硬凑的求面积体积的题用到三阶行列式外,没有一 个问题真正要算三阶以上行列式的,花了很多学时讲的各种行列式理论和方法竟然没用处。原 因何在?这是因为用消元法解方程时,已经用主元都不为零判定了解的存在和唯一,不知不觉 中已用了主元连乘定义下行列式;不必另起炉灶,让学生去学其他两种繁琐的高阶行列式定义, 也用不到克拉默法则。主元连乘法是高斯消元的自然延伸,不引进新概念新名词,并可很容易 地证明行列式的各种有用的性质,也是软件编程的依据。 对于工程人才,数学定义和方法的可实现性是必须关注的问题。数值计算中通常用所需的 乘法次数来标志计算的复杂度,下表给出了行列式三种定义方法在不同阶数下的计算量比较 表 3-1 行列式的三种定义方法所需乘法次数 阶数 n 2 3 4 5 10 25 1. 显式法(不含正负号计算) (n-1)n! 2 12 72 480 32659200 3.72*10^26 2. 代数余子式法≈2n! 2 9 40 205 7257600 3.10*10^25 3. 对角主元连乘法 n 3 /3 4 13 24 45 342 5233 拿 1,3 两种方法所需的乘法次数加以比较,可以看出,只有 n=2 时,用显式法求行列式才 比消元法方便。当 n=10 时,用显式法算的计算量为三千万次,主元连乘法才 342 次。n 更大 时,两种老定义的运算量不仅超越了人们笔算可能性,也超越了计算机的能力。这种现象称为 “维数灾难(Curse of Dimensionality)”。在新定义下,不但计算量大大缩减,那些“逆序 数、代数余子式、随伴矩阵、行列式按行展开、…”等等只能给爱数学的人练练推导,根本没 有实用价值。非数学系避开了这些“拦路虎”,可大大压缩篇幅,降低难度,何乐而不为呢。 不讲这些概念水平就低吗?其实这才是有水平:高屋建瓴,看透了传统定义的致命痼疾, 让后人别白费时间。经典的行列式定义出现最早,最繁琐,围绕它的公式也多,但只能推导不 能算;高斯消元法可直接得出行列式的主元连乘公式,计算很简单,有人就把简化说成水平低, 宁可用繁琐的老定义加上复杂的推导来绕圈子,非要繁才算高水平;这是荒唐的逻辑。好在到 了计算机时代,编程中自然会扬弃一切无用的中间环节。所以 MATLAB 中就没有这些繁琐过 时的术语及其子程序。当前全世界有几百万教学、科研和工程用户都在靠它解大规模、高难度 的线性代数问题,说明从应用出发,确实不需要这些概念。美国 MIT 的教材[3]也不细讲这些 术语,只通过二、三阶矩阵简单介绍了一下。 好比登山,老定义是靠手工攀岩,要一尺一尺地爬。高斯法找到了筑台阶的办法,可以一 级一级地走;计算机相当于发明缆车,可以一步到顶。根据非数学专业学生的基础和面临的实 际问题,该教什么是不言自明的。让少数数学系的学生练两天攀岩也许还有点道理,让千百万 非数学系的学生都去学攀岩,不坐缆车,实在讲不过去。 四、向量空间要讲透三维,减缩 N 维

帮助大学低年级学生建立立体概念是大学教学计划中的重要一环,为此有制图、画法几何 多变量微积分、物理中场的演示、数学中的场论、电工中的复信号、电机中的旋转磁场等等多 门课程,说明三维空间的概念不是那末好建立的。线性代数本应该有责任帮助学生建立空间概 含,但现有教法知品化三维,村分强调N维空间。国外的各种面向工科的线性代数代委教材 都是以三维空间为主的,并且有大量的立体图辅助。中国教材强调N维,全是公式,没法画 图,很不利于学生接受。我们强调二、 三维,使例子形象化,并使图形作为建立概念的重要 具。利用三维空间向量的概念又可以推导出超定方程组的最小二乘解,为扩大线性代数的应用 领域起了很好的作用。 强化和讲透三维可通过许多应用实例来实现,例如在三维空间中如何认识欠定方程组和超 定方程组的解,如何认识和应用坐标变换、投影和QR分解等。N维只用于解方程组,不用于 向量空间,这也是和传统教材的区别。不是说N维不 重要,而是说要循序渐进,先感性积累 后理性抽象,按美国改革线性代数的第(W)点,N维应另设后续课程来讲。 五、弱化次定,加强超定。 欠定方程组是由于命题条件不足造成的,工程师可以拒绝处理,在强调解的存在和唯一性 的高等数学入门阶段,找不到基础解系的工程实例,不可能让学生理解其意义,在此让大学新 生花很多学时是太超前】 。超定 方程则是工程上常见的问,它来源于实践中不可避免的干扰 和测量误差,而且其证明又可加强向量空间概念。世界各国的教材都讲,只有我国的教材不讲 大量的应用命题就不会解。“大讲欠定,不讲超定”是我国线性代数教学脱离工程的突出表现。 有用的不讲,讲的却没用,浪费了很多课时,对工程应用完全没有帮助。 六、特征根的意义和解法不讲高阶,只讲到两阶为止,但实数和复数根都要讲。 实际上三阶及以上的特征根,多数老师都不会笔算,也没有 本教材讲它的求法。应该老 老实实告诉学生 三阶以上系统的特征值问题 手工解是不行的, 只有依靠计算机。 二次型 以只讲到二阶,高阶实二次型不但计算有难度,而且很难找其物理意义和几何模型,更谈不上 工程应用。而复数特征根却是工程中很有用的。它是理解振动问题的基础,它是学生在日常经 验中能够接受的。 采用了这些改革措施后,理论是大大减少了,新教2只用了100多而的篇幅。就打下了 初步的理论基础,足以解决所列举的几十个线性代数问题。这些问题中 的四分 用现在教 线性代数是很难解或解不出的,用最小的学习成本以获得最大的应用效果,这是内容改革的目 标。原有的线性代数书为什么解不了这些题呢?(1)因为不用计算机,表中十几个超过三阶 的题目就很难解,甚至无法解:即使是三阶题,手工解起来也是少慢差费:(2)因为空间概 今不清,对干空间多点共面性、刚体云动和华标变撩方面的颗日就感闲难:(3)因为不进招 定方程,几个超定命题也不 (4)不讲复数特征值,振动问题也不会解。可见我们删 的内容完全不影响学生解工程问题的能力,只是减少了工程上用不到(可惜考研有些还要)的 数学推演,增补的内容却都是有的放矢地提高了解决多种应用问题的能力。 需要说明的是,上述改革是针对大学生和工程师提出的理论上的最低要求,比较合适于学 时数0左右,培养目标为应用型、技能型的专业,并且不参加现在的考研。对于理工科中研 究型人才培养,除了达到最低要求外,要根据各专业的需要和大纲所给的学时,适当地加强 些理论以应付考研 但实践也要加强。对计算速度和精度的讨论、对 三维空间概念的强化 对 超定方程解法、对复数特征根、对应用问题的建模、对用MATLAB解题的能力、,总之, 在线性代数建模和实践环节上,都应该有适应工科需求的变革与加强。 参考文献 [1]A.Tucker.The Growing Importance of Linear Algebra in Undergraduate Mathematics,Resources for Teaching Linear Algebra.MAANote Series 42.199 ]陈怀踩,实用大众线性代数(MATLAB版),西安电子科技大学出版社,2014年7月
帮助大学低年级学生建立立体概念是大学教学计划中的重要一环,为此有制图、画法几何、 多变量微积分、物理中场的演示、数学中的场论、电工中的复信号、电机中的旋转磁场等等多 门课程,说明三维空间的概念不是那末好建立的。线性代数本应该有责任帮助学生建立空间概 念,但现有教法却弱化三维,过分强调 N 维空间。国外的各种面向工科的线性代数优秀教材, 都是以三维空间为主的,并且有大量的立体图辅助。中国教材强调 N 维,全是公式,没法画 图,很不利于学生接受。我们强调二、三维,使例子形象化,并使图形作为建立概念的重要工 具。利用三维空间向量的概念又可以推导出超定方程组的最小二乘解,为扩大线性代数的应用 领域起了很好的作用。 强化和讲透三维可通过许多应用实例来实现,例如在三维空间中如何认识欠定方程组和超 定方程组的解,如何认识和应用坐标变换、投影和 QR 分解等。N 维只用于解方程组,不用于 向量空间,这也是和传统教材的区别。不是说 N 维不重要,而是说要循序渐进,先感性积累, 后理性抽象,按美国改革线性代数的第(v)点,N 维应另设后续课程来讲。 五、弱化欠定,加强超定。 欠定方程组是由于命题条件不足造成的,工程师可以拒绝处理,在强调解的存在和唯一性 的高等数学入门阶段,找不到基础解系的工程实例,不可能让学生理解其意义,在此让大学新 生花很多学时是太超前了。超定方程则是工程上常见的问题,它来源于实践中不可避免的干扰 和测量误差,而且其证明又可加强向量空间概念。世界各国的教材都讲,只有我国的教材不讲, 大量的应用命题就不会解。“大讲欠定,不讲超定”是我国线性代数教学脱离工程的突出表现。 有用的不讲,讲的却没用,浪费了很多课时,对工程应用完全没有帮助。 六、特征根的意义和解法不讲高阶,只讲到两阶为止,但实数和复数根都要讲。 实际上三阶及以上的特征根,多数老师都不会笔算,也没有一本教材讲它的求法。应该老 老实实告诉学生,三阶以上系统的特征值问题,手工解是不行的,只有依靠计算机。二次型可 以只讲到二阶,高阶实二次型不但计算有难度,而且很难找其物理意义和几何模型,更谈不上 工程应用。而复数特征根却是工程中很有用的。它是理解振动问题的基础,它是学生在日常经 验中能够接受的。 采用了这些改革措施后,理论是大大减少了,新教材[2]只用了 100 多页的篇幅,就打下了 初步的理论基础,足以解决所列举的几十个线性代数问题。这些问题中约四分之一用现在教的 线性代数是很难解或解不出的,用最小的学习成本以获得最大的应用效果,这是内容改革的目 标。原有的线性代数书为什么解不了这些题呢?(1)因为不用计算机,表中十几个超过三阶 的题目就很难解,甚至无法解;即使是三阶题,手工解起来也是少慢差费;(2)因为空间概 念不清,对于空间多点共面性、刚体运动和坐标变换方面的题目就感困难;(3)因为不讲超 定方程,几个超定命题也不会解;(4)不讲复数特征值,振动问题也不会解。可见我们删除 的内容完全不影响学生解工程问题的能力,只是减少了工程上用不到(可惜考研有些还要)的 数学推演,增补的内容却都是有的放矢地提高了解决多种应用问题的能力。 需要说明的是,上述改革是针对大学生和工程师提出的理论上的最低要求,比较合适于学 时数 30 左右,培养目标为应用型、技能型的专业,并且不参加现在的考研。对于理工科中研 究型人才培养,除了达到最低要求外,要根据各专业的需要和大纲所给的学时,适当地加强一 些理论以应付考研,但实践也要加强。对计算速度和精度的讨论、对三维空间概念的强化、对 超定方程解法、对复数特征根、对应用问题的建模、对用 MATLAB 解题的能力、...,总之, 在线性代数建模和实践环节上,都应该有适应工科需求的变革与加强。 参考文献: [1] A. Tucker, The Growing Importance of Linear Algebra in Undergraduate Mathematics, Resources for Teaching Linear Algebra. MAA Note Series 42, 1997 [2] 陈怀琛,实用大众线性代数(MATLAB 版),西安电子科技大学出版社,2014 年 7 月

[3]Gilbert Strang Introduction to Linear Algebra.4th Edition.Wilsley-Cabridge Press,Feb.2009 1SBN:978-098023271 「4】钱学森,回顾与展望,《老交大的故事》,江苏人民出版社,1989 附录:教材《实用大众线性代数(MATLAB版)》中的应用实例汇总表
[3] Gilbert Strang, Introduction to Linear Algebra, 4th Edition, Wilsley-Cambridge Press, Feb.2009, ISBN: 978-098023271 [4] 钱学森,回顾与展望,《老交大的故事》,江苏人民出版社,1989 附录:教材《实用大众线性代数(MATLAB 版)》中的应用实例汇总表

序号 例题名称 炬阵阶数 方程类型向量空间线性变换 矩阵运算 页数 1 例1.8插值多项式 4 适定 22 2 例1.9平板稳态温度的计算 4 适定 22 3 例1.10交通流量的分析 4 欠定 补充其他条件求解 23 4 例1.11化学方程的配平 3 欠定 补充其他条件求解 23 5 例2.14成本核算问题 3 矩阵乘法 42 6 例2.15列乘行生成网格矩阵 10×21 矩阵乘法 43 7 例2.16 Vander矩阵的生成 4*4 矩阵乘法 43 8 例2.17特殊矩阵的生成 4 求逆阵 43 9 例2.18图及其矩阵表述 4 矩阵乘法 44 10 例2.19网络的矩阵分割和连接 2X2 矩阵乘法 45 11 例2.20微分矩阵和积分矩阵 3 求逆阵 46 12 例3.7用行列式判解的存在性 4 行列式计算 58 13 例3.8行列式为零时无逆阵 3 求逆阵 59 14 例3.9用行列式计算面积 2 行列式计算 59 15 例3.10特征行列式的计算 2 行列式计算 60 16 例4.7欠定方程解的几何意义 2×3 欠定 空间概念 75 17 例4.8超定方程解的几何意义 3×1 超定 空间概念 76 18 例4.9超定方程解的几何意义 3X2 超定 空间概念 77 19 例4.6.1减肥配方的实现 3 适定 78 20 例4.6.2三维空间中的平面方程 3 空间概念 79 21 例4.6.3价格平衡模型 适定 81 22 例4.6.4混凝土配料中的应用 5 超定 82 23 例5.1平面线性变换的几何意义 2 空间概念线性变换 88 24 例5.2斜体字母生成 2 空间概念线性变换 91 25 例5.3刚体平面运动 3 空间概念线性变换 93 26 例5.5测量数据直线性判断 4×2 超定 空间概念线性变换 99 27 例5.6.1字母阴影投影的生成 2 线性变换 102 28 例5.6.2雷达坐标与地面坐标系 3 正交线性变换 103 29 例5.6.3人口迁徙模型 2 矩阵幂次 实特征根 104 30 例5.6.4物料混合问题 2 微分方程矩阵指数 实特征根 105 31 例5.6.5 单自由度机械振动 2 微分方程矩阵指数 复特征根 107 32 例6.1电阻电路的计算 3 适定 111 33 例6.2交流稳态电路的计算 3 适定 复数矩阵 112 34 例63双杆系统的支撑反力 6 适定 113 35例6.4双滑块动力学系统 4 适定 113 36 例6.5 信号流图和梅森公式 3 适定 符号运算公式推导 114 37 例6.6数字滤波器系统函数 6 适定 116 38 例6.7空间五点共面的分析 3×5 超定 QR分解 117 39 例6.8,圆锥截面插值问题 5 适定超定 118 40 例6.9舰载机测定甲板偏转角 2 QR分解 119 41 例6.10坐标测量仪检验圆形 7×3 超定 119 42 例6.11三角形运动连续化 3 线性变换 方阵分数幂 123 43 例6.12控制系统结构图的化简 5×5 适定 符号运算公式推导 124 44 例6.13机械臂速度和雅可比矩 2×2 公式推导线性变换 125 45 例6.14情报检索模型 7×6 矩阵乘法 125 46 例6.15宏观经济模型 3 适定 127
序号 例题名称 矩阵阶数 方程类型 向量空间线性变换 矩阵运算 页数 1 例 1.8 插值多项式 4 适定 22 2 例 1.9 平板稳态温度的计算 4 适定 22 3 例 1.10 交通流量的分析 4 欠定 补充其他条件求解 23 4 例 1.11 化学方程的配平 3 欠定 补充其他条件求解 23 5 例 2.14 成本核算问题 3 矩阵乘法 42 6 例 2.15 列乘行生成网格矩阵 10×21 矩阵乘法 43 7 例 2.16 Vander 矩阵的生成 4*4 矩阵乘法 43 8 例 2.17 特殊矩阵的生成 4 求逆阵 43 9 例 2.18 图及其矩阵表述 4 矩阵乘法 44 10 例 2.19 网络的矩阵分割和连接 2×2 矩阵乘法 45 11 例 2.20 微分矩阵和积分矩阵 3 求逆阵 46 12 例 3.7 用行列式判解的存在性 4 行列式计算 58 13 例 3.8 行列式为零时无逆阵 3 求逆阵 59 14 例 3.9 用行列式计算面积 2 行列式计算 59 15 例 3.10 特征行列式的计算 2 行列式计算 60 16 例 4.7 欠定方程解的几何意义 2×3 欠定 空间概念 75 17 例 4.8 超定方程解的几何意义 3×1 超定 空间概念 76 18 例 4.9 超定方程解的几何意义 3×2 超定 空间概念 77 19 例 4.6.1 减肥配方的实现 3 适定 78 20 例 4.6.2 三维空间中的平面方程 3 空间概念 79 21 例 4.6.3 价格平衡模型 3 适定 81 22 例 4.6.4 混凝土配料中的应用 5 超定 82 23 例 5.1 平面线性变换的几何意义 2 空间概念线性变换 88 24 例 5.2 斜体字母生成 2 空间概念线性变换 91 25 例 5.3 刚体平面运动 3 空间概念线性变换 93 26 例 5.5 测量数据直线性判断 4×2 超定 空间概念线性变换 99 27 例 5.6.1 字母阴影投影的生成 2 线性变换 102 28 例 5.6.2 雷达坐标与地面坐标系 3 正交线性变换 103 29 例 5.6.3 人口迁徙模型 2 矩阵幂次 实特征根 104 30 例 5.6.4 物料混合问题 2 微分方程矩阵指数 实特征根 105 31 例 5.6.5 单自由度机械振动 2 微分方程矩阵指数 复特征根 107 32 例 6.1 电阻电路的计算 3 适定 111 33 例 6.2 交流稳态电路的计算 3 适定 复数矩阵 112 34 例 6.3 双杆系统的支撑反力 6 适定 113 35 例 6.4 双滑块动力学系统 4 适定 113 36 例 6.5 信号流图和梅森公式 3 适定 符号运算公式推导 114 37 例 6.6 数字滤波器系统函数 6 适定 116 38 例 6.7 空间五点共面的分析 3×5 超定 QR 分解 117 39 例 6.8 . 圆锥截面插值问题 5 适定超定 118 40 例 6.9 舰载机测定甲板偏转角 2 QR 分解 119 41 例 6.10 坐标测量仪检验圆形 7×3 超定 119 42 例 6.11 三角形运动连续化 3 线性变换 方阵分数幂 123 43 例 6.12 控制系统结构图的化简 5×5 适定 符号运算公式推导 124 44 例 6.13 机械臂速度和雅可比矩 阵 2×2 公式推导线性变换 125 45 例 6.14 情报检索模型 7×6 矩阵乘法 125 46 例 6.15 宏观经济模型 3 适定 127