
第二章 时域中的离散信号和系统 1
1 第二章 时域中的离散信号和系统

2.1模拟信号与其采样序列 ·对模拟信号xa(t)以采样周期T进行等间隔采样, 得到采样序列xn) x(m)=xa(l=nr=xa(nTb -0<n<0 ·它的每一个样本点与相应处的模拟信号值相等, 而在其它时间位置处的值为零。 ·这一采样序列与原来的模拟信号是不等价的: 不包围面积,量纲不同,物理作用不同。 2
2 2.1 模拟信号与其采样序列 • 对模拟信号 以采样周期T进行等间隔采样, 得到采样序列x(n) • 它的每一个样本点与相应处的模拟信号值相等, 而在其它时间位置处的值为零。 • 这一采样序列与原来的模拟信号是不等价的: 不包围面积,量纲不同,物理作用不同。 x (t) a = = − = x n x t xa nT n a t n T ( ) ( ) ( )

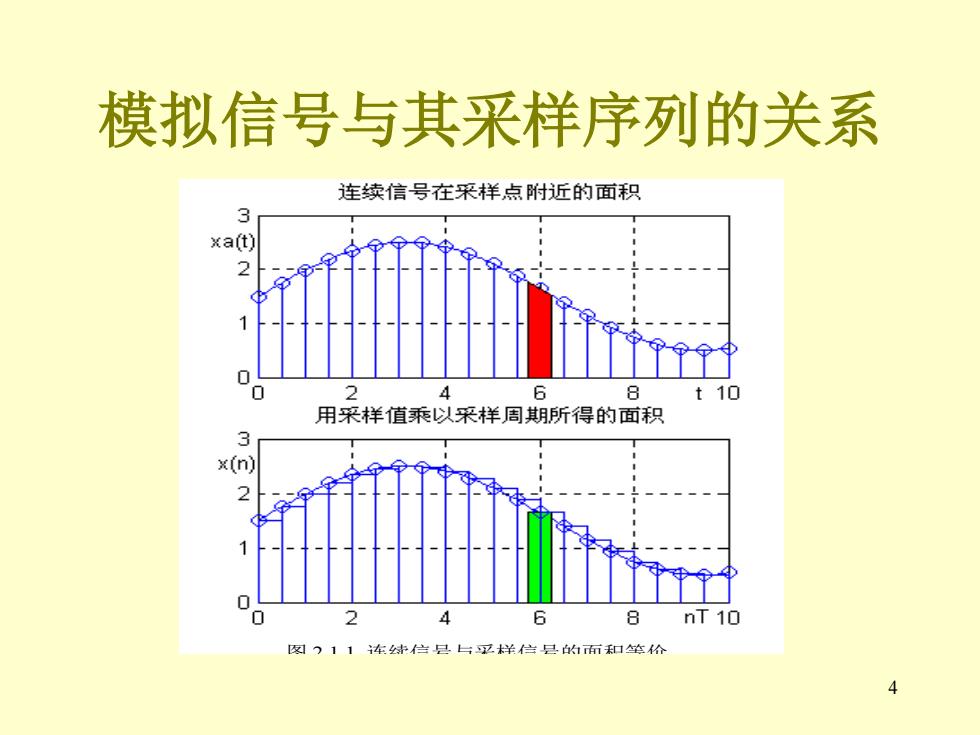
模拟信号与其采样序列的关系 。 要构成一个与模拟信号有等价性的离散序列, 应该有 xe(n)=T.x(n)=T.xa(nT) ·这个序列xe(n)具有面积的量纲,T很密时,有 limx(n)=T·x,(以,nr=宽度T所围面积 T>0 因此和原始的模拟信号等价。 ·这个关系式不难从图2.1.1中得到验证 3
3 模拟信号与其采样序列的关系 • 要构成一个与模拟信号有等价性的离散序列, 应该有 • 这个序列 具有面积的量纲,T很密时,有 因此和原始的模拟信号等价。 • 这个关系式不难从图2.1.1中得到验证 x (n) T x(n) T x (nT) e a = = x (n) e 0 ( ) ( ) lim e a t nT T x n T x t T = → = =宽度 所围面积
模拟信号与其采样序列的关系 连续信号在采样点附近的面积 3 xa(t) 2 0 6 t10 用采样值乘以采样周期所得的面积 3 x(n 6 8 nT 10 凤)11在续信是与平样信是的而如笔价 4
4 模拟信号与其采样序列的关系 图 2.1.1 连续信号与采样信号的面积等价

模拟信号与其采样序列的关系 ·人们用(2.1.1)式的序列作为离散信号 的研究模型,由于抽掉了模拟信号中的 主要物理量一时间。在数字域处理信 号时可只按序号逐次进行运算和存储, 这就是抽象为序列模型的好处。 另一方面必须看到模型与原物理过程之 间的本质差异。在把序列与模拟信号进 行转换和等价比较的时候,必需按等价 序列x。(n)的概念(2.1.2)式来考虑
5 模拟信号与其采样序列的关系 • 人们用(2.1.1)式的序列作为离散信号 的研究模型,由于抽掉了模拟信号中的 主要物理量——时间。在数字域处理信 号时可只按序号逐次进行运算和存储, 这就是抽象为序列模型的好处。 • 另一方面必须看到模型与原物理过程之 间的本质差异。在把序列与模拟信号进 行转换和等价比较的时候,必需按等价 序列xe(n)的概念(2.1.2)式来考虑

2.2基本序列及其运算 ·序列的表示方法 完全地表示序列x(n)要用x和n两个向量,x表示序 列的值,n表示它的位置或时间次序。 ·例如x(n)={2,1.2,-1.4,3,1,4,3.1,7}(下划双 线表示n=0处的采样点) -用MATLAB表示时用两个向量: n=[-3,-2,-1,0,1,2,3,4]; x=[2,1.2,-1.4,3,1,4,3.1,7]; 可见n是顺序增加的整数序列,可写成n=ns:nf, 序列的长度为lx=nf-ns+1。本例n=-3:4;lx=8。 6
6 2.2 基本序列及其运算 • 序列的表示方法 –完全地表示序列x(n)要用x和n两个向量,x表示序 列的值,n表示它的位置或时间次序。 • 例如x(n)={2,1.2,-1.4,3,1,4,3.1,7}(下划双 线表示n=0处的采样点) –用MATLAB表示时用两个向量: n = [-3,-2,-1,0,1,2,3,4]; x = [2,1.2,-1.4,3,1,4,3.1,7]; 可见n是顺序增加的整数序列,可写成n=ns:nf, 序列的长度为lx=nf-ns+1。本例n= -3:4;lx=8

基本序列及其运算 ·有限长序列和无限长序列 一序列位置向量的起点和终点都是有限数称为有限长 序列 一序列位置向量的起点向-∞延伸为无限长序列,简 称左序列。 一序列位置向量的终点向∞延伸也为无限长序列,简 称右序列。 工程中遇到的序列都属于有限序列,有些情况下可看 成右序列,但不会有左序列。 复数序列可分解为实部和虚部两个实数序列 7
7 基本序列及其运算 • 有限长序列和无限长序列 – 序列位置向量的起点和终点都是有限数称为有限长 序列 – 序列位置向量的起点向-∞ 延伸为无限长序列,简 称左序列。 – 序列位置向量的终点向∞ 延伸也为无限长序列,简 称右序列。 工程中遇到的序列都属于有限序列,有些情况下可看 成右序列,但不会有左序列。 复数序列可分解为实部和虚部两个实数序列

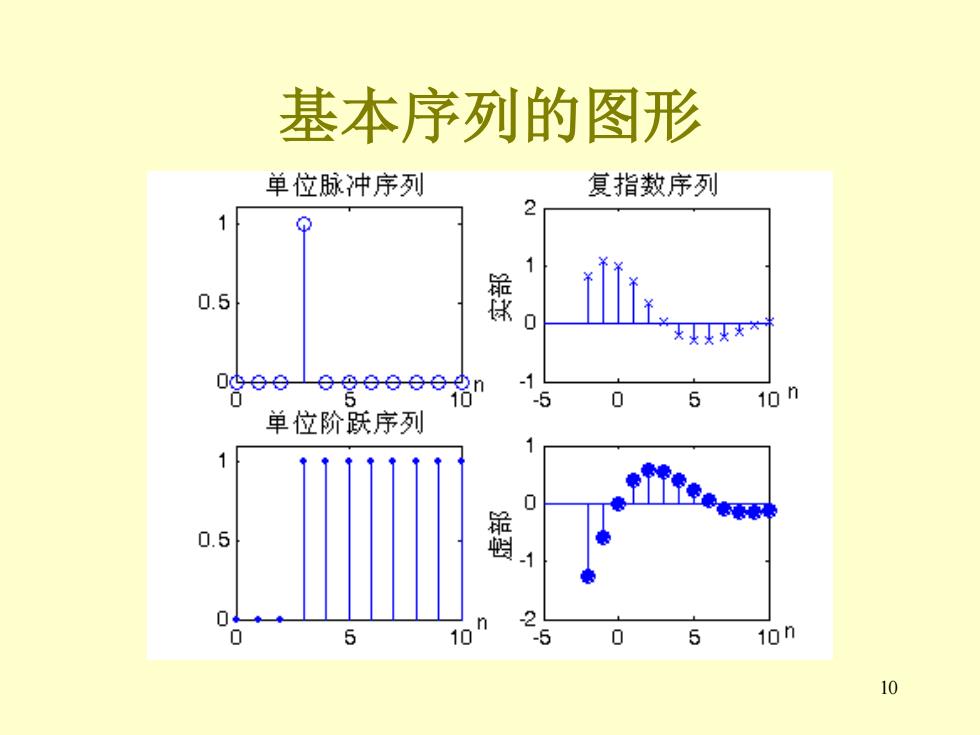
常用的典型序列 ·单位脉冲序列δ(n) [x,n]impseq(np,ns,nf) ·单位阶跃序列μ(n) [x,n]stepseq(np,ns,nf) ·矩形序列 Ry(n)=L(n)-u(n-N) ·复数指数序列 x =e(atjo)n ·正余弦序列 x(n)=cos(on)+jsin(on)=ejom 8
8 • 单位脉冲序列δ(n) [x,n] = impseq(np,ns,nf) • 单位阶跃序列μ(n) [x,n] = stepseq(np,ns,nf) • 矩形序列 • 复数指数序列 • 正余弦序列 x(n)=cos(ωn)+jsin(ωn) 常用的典型序列 ( ) ( ) ( ) R n n n N N = − − ( ) j n x e + = j n e =

单位脉冲序列的函数程序 function [x,n]impseq(np,ns,nf) %ns为序列起始位置,nf为序列终止位置, np为脉冲位置 if ns>np ns>nf np>nf error(’输入位置参数不满足ns=0]
9 • function [x,n] = impseq(np,ns,nf) % ns为序列起始位置,nf为序列终止位置, np为脉冲位置 if ns>np | ns>nf | np>nf error(’输入位置参数不满足ns = 0] 单位脉冲序列的函数程序
基本序列的图形 单位脉冲序列 复指数序列 2 0.5 腰 0 0g66ogs96e鼎n -5 10n 单位阶跃序列 0 0.5 福 0 2 0 5 10 5 10n 10
10 基本序列的图形