
第四章 信号频谱的高效计算 1
1 第四章 信号频谱的高效计算

信号频谱的高效计算 。4.1 各种傅立叶变换及其关系 。4.2 快速付立叶变换(FFT) ·4.3 用FFT计算序列的频谱 ·4.4 时域采样中的频谱变换 。4.5 连续信号的频谱计算 ·4.6用反变换从频谱计算信号 ·4.7用FFT计算能量 ·4.8小结 2
2 信号频谱的高效计算 • 4.1 各种傅立叶变换及其关系 • 4.2 快速付立叶变换(FFT) • 4.3 用FFT计算序列的频谱 • 4.4 时域采样中的频谱变换 • 4.5 连续信号的频谱计算 • 4.6 用反变换从频谱计算信号 • 4.7 用FFT计算能量 • 4.8 小结

4.1各种傅立叶变换及其关系 (1)时域的周期性对应于频域的离散化。 (2)时域的离散化对应于频域的周期性。其主 周期就是乃奎斯特频率范围[-π/T,π/T]。 (3)周期性的离散序列将对应于离散并周期性 的频谱。即离散傅立叶级数(DFS)。离散有利 于数值计算,但信号无穷延伸又不利于计算。 (4)把时域和频域数据长度都限于主周期,并 且使之相等,形成离散傅立叶变换(DFT)。它 既离散,又长度有限,适合于计算机数值计算。 3
3 (1)时域的周期性对应于频域的离散化。 (2) 时域的离散化对应于频域的周期性。其主 周期就是乃奎斯特频率范围[-π/T,π/T]。 (3) 周期性的离散序列将对应于离散并周期性 的频谱。即离散傅立叶级数(DFS)。离散有利 于数值计算,但信号无穷延伸又不利于计算。 (4)把时域和频域数据长度都限于主周期,并 且使之相等,形成离散傅立叶变换(DFT)。它 既离散,又长度有限,适合于计算机数值计算。 4.1 各种傅立叶变换及其关系
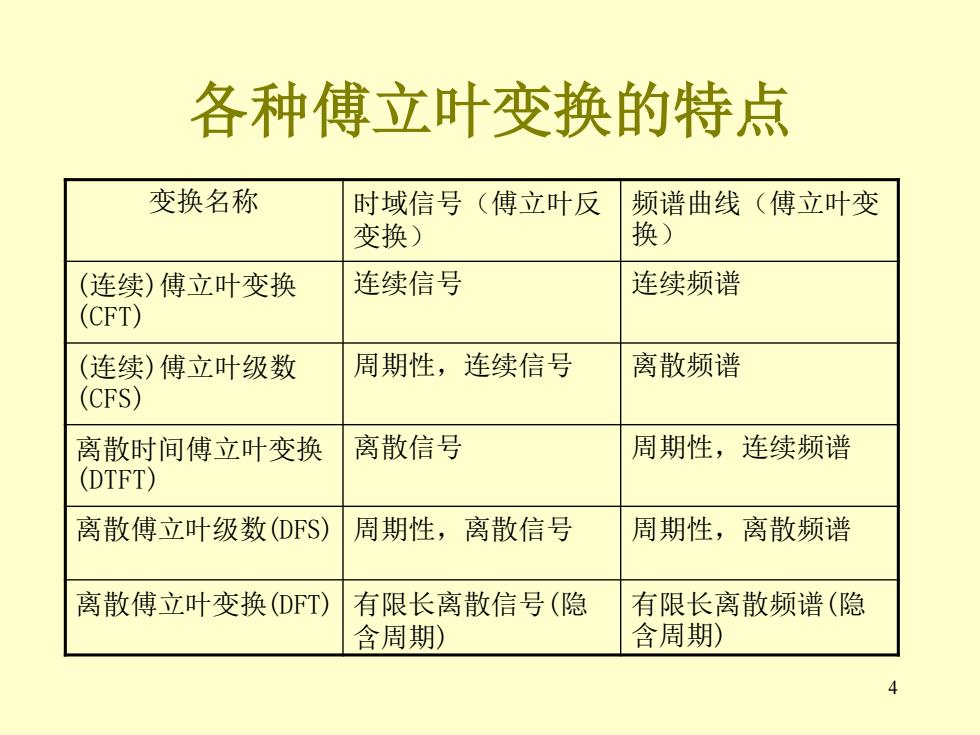
各种傅立叶变换的特点 变换名称 时域信号(傅立叶反 频谱曲线(傅立叶变 变换) 换) (连续)傅立叶变换 连续信号 连续频谱 (CFT) (连续)傅立叶级数 周期性,连续信号 离散频谱 (CFS) 离散时间傅立叶变换 离散信号 周期性,连续频谱 (DTFT) 离散傅立叶级数(DFS) 周期性,离散信号 周期性,离散频谱 离散傅立叶变换(DFT) 有限长离散信号(隐 有限长离散频谱(隐 含周期) 含周期)
4 各种傅立叶变换的特点 变换名称 时域信号(傅立叶反 变换) 频谱曲线(傅立叶变 换) (连续)傅立叶变换 (CFT) 连续信号 连续频谱 (连续)傅立叶级数 (CFS) 周期性,连续信号 离散频谱 离散时间傅立叶变换 (DTFT) 离散信号 周期性,连续频谱 离散傅立叶级数(DFS) 周期性,离散信号 周期性,离散频谱 离散傅立叶变换(DFT) 有限长离散信号(隐 含周期) 有限长离散频谱(隐 含周期)

各种傅立叶变换及其相互关系 对离散傅立叶变换(DFT),人们开发了可以高效 地进行计算的方法,称为快速傅立叶变换 (FFT)。 人们想尽量利用F℉T来解决其他类型信号的频谱 计算问题。所以要充分弄清各种傅立叶变换之 间的关系。本章就讨论这个主题。先把主要结 果列出,其中有些结论已经讨论过,与采样定 理有关的结论将在后面讨论,读者可先接受下 来。目的是走通下图的路线,完成时频域傅立 叶变换的数值计算。 5
5 对离散傅立叶变换(DFT),人们开发了可以高效 地进行计算的方法,称为快速傅立叶变换 (FFT)。 人们想尽量利用FFT来解决其他类型信号的频谱 计算问题。所以要充分弄清各种傅立叶变换之 间的关系。本章就讨论这个主题。先把主要结 果列出,其中有些结论已经讨论过,与采样定 理有关的结论将在后面讨论,读者可先接受下 来。目的是走通下图的路线,完成时频域傅立 叶变换的数值计算。 各种傅立叶变换及其相互关系

各种傅立叶变换及其相互关系 模拟信号 时域采样 周期延拓 主值区间 时域x()—n) x(n)— x(n)RN(n) (FFT) 频域XaGj2)—X(j2) (k) —X(k)RN(k) CTFT DTFT DFS DFT ICTFT IDTFT 频域采样 IDFT 6
6 各种傅立叶变换及其相互关系 模拟信号 时域采样 周期延拓 主值区间 时域xa(t) —— x(n) —— ——x(n)·RN(n) | | (FFT) 频域Xa(jΩ)——X(jΩ)—— ——X(k)·RN(k) CTFT DTFT DFS DFT ICTFT IDTFT 频域采样 IDFT x n( ) X k( )

各种傅立叶变换及其相互关系 (1).DFT与DFS的关系: X(k)=ak·N或 a4= (4.1.7 N (2).DFT与DTFT的关系 采样 w号)o器 插补 Xo)=∑X(h)m(N2z2eNka k-0 sin(oN-2πk)/2N) >
7 各种傅立叶变换及其相互关系 (1). DFT与DFS的关系: 或 (4.1.7) (2). DFT与DTFT的关系 : 采样 插补 N X k ak ( ) X(k) = ak N = ( ) NT k X NT X k X k 2 2 ( ) = = = ( ) (2 / )( 1)/ 2 1 0 sin(( 2 )/ 2 ) sin(( 2 )/ 2) ( ) 1 − − − − = − − = j k N N N k e N k N N k X k N X

各种傅立叶变换及其相互关系 (3).DTFT与CTFT的关系:用采样定理或乃奎 斯特定理建立关系。由CTFT求DTFT x@,-三x(n-)-号 由DTFT求CTFT:频率泄漏可以忽略不计时近 似解。 x号-l飞a o≤π 8
8 各种傅立叶变换及其相互关系 (3). DTFT与CTFT的关系:用采样定理或乃奎 斯特定理建立关系。由CTFT求DTFT 由DTFT求CTFT:频率泄漏可以忽略不计时近 似解。 1 2 ( ) , a k X X k T T T =− = − = ( ) ( ) ( ) 0 a a T X X FT x t T =

各种傅立叶变换及其相互关系 ·DFT与CTFT的相互关系: 由CTT求DFT只是取出其一部分,没有误差问题。 而由DFT求CTFT要先经过由DFT求DTFT,再经 过由DTFT求CTFT的两步。由离散求连续不一定 有解,只有在信号的频谱足够窄,频率泄漏可 以忽略不计的条件才可能近似由下式求得。 X(k) aka≈ak= 9
9 各种傅立叶变换及其相互关系 • DFT与CTFT的相互关系: 由CTFT求DFT只是取出其一部分,没有误差问题。 而由DFT求CTFT要先经过由DFT求DTFT,再经 过由DTFT求CTFT的两步。由离散求连续不一定 有解,只有在信号的频谱足够窄,频率泄漏可 以忽略不计的条件才可能近似由下式求得。 2 1 2 ( ) N k N N X k ak a ak = − +

4.2快速付立叶变换(FFT) 计算DFT的运算次数按N2快速增长。设N可以被2整除, 把x(n)分成两个子序列x1(n)和x2(n), x(n)=[x(0),x(2),…x(W-2)] n=0,…,(N-1)/2 x2(n)=[x(1),x(3),…(N-1)] 则原序列的DFT可写成(设N1=N/2): X(m)=x(0)W8+x(2)W2m+…+x(N-2)W-2》m+ +x(1)W+x(3)Wm+...+x(N-1)WW-Im =Ow8+w%++x1(N1-Dw-m+ +[xO)W9+x2④w双++x2(W1-1)w-m 10
10 4.2 快速付立叶变换(FFT) • 计算DFT的运算次数按N 2快速增长。设N可以被2整除, 把x(n)分成两个子序列x1(n)和x2(n), 则原序列的DFT可写成(设N1=N/2): 1 2 ( ) [ (0), (2), ( 2)] 0, ,( 1) / 2 ( ) [ (1), (3), ( 1)] x n x x x N n N x n x x N = − = − = − 0 2 ( 2 3 ( 1) ( ) (0) (2) ( 2) (1) (3) ( 1) m N m N N N m m N m N N N X m x W x W x N W x W x W x N W − − = + + + − + + + + + − ) N m N m N N m N N m N m N N W x W x W x N W x W x W x N W ( 1) 2 2 1 0 2 ( 1) 1 1 1 0 1 1 1 1 1 1 1 1 1 [ (0) (1) ( 1) (0) (1) ( 1) − − + + + + − = + + + − +