
5.3节数列和级数
5.3节 数列和级数

一.数列的表示方法 。 数列就是自变量为整数时的函数。MATLAB中的元 素群运算特别适合于简明地表达数列,可省去其他 语言中的循环语句。下面就是二些例子: ·n=1:6; ·1./m=1.00000.50000.33330.25000.20000.1667 ·(-1).n./m=-1.00000.5000-0.33330.2500-0.20000.1667 。 1./m./n+1)=0.50000.16670.08330.05000.03330.0238 左端的算式表示这个数列产生方法的“通项”,它 坐须符食元素群运算的规则、厅以要充分注意用泰 乘、点除和点幕。例如(1).n就是产生交项薮列符 号位的算式,它在n取偶数时为正,而它在n取奇 数时为负。在某些情况下,当产生数列的运算中包 含数组运算时,就不可避免地要用for循环
一.数列的表示方法 • 数列就是自变量为整数时的函数。MATLAB中的元 素群运算特别适合于简明地表达数列,可省去其他 语言中的循环语句。下面就是一些例子: • n=1:6; • 1./n = 1.0000 0.5000 0.3333 0.2500 0.2000 0.1667 • (-1).^n./n = -1.0000 0.5000 -0.3333 0.2500 -0.2000 0.1667 • 1./n./(n+1) = 0.5000 0.1667 0.0833 0.0500 0.0333 0.0238 • 左端的算式表示这个数列产生方法的“通项”,它 必须符合元素群运算的规则,所以要充分注意用点 乘、点除和点幂。例如(-1).^n就是产生交项数列符 号位的算式,它在n取偶数时为正,而它在n取奇 数时为负。在某些情况下,当产生数列的运算中包 含数组运算时,就不可避免地要用for 循环

数列用for循环的表示方法 ·比如计算n!(n的阶乘),它应该写成prod(1:n), 其中的n就不能是数组,因为prod(1:n)中已用了数 组[1n]。这时必须用: for k=1:6 x(k)=1/prod(1:k);end,x ·得x=1.00000.50000.1667 0.0417 0.00830.0014 ·在MATLAB中数列随n增加而变化的趋向很容易由 计算其数值并作图的方法来解决。但要求数列在 趋向∞时的极限时往往要藉助于符号数学,可以 从下面的实例看出
数列用for循环的表示方法 • 比如计算n!(n的阶乘),它应该写成prod(1:n), 其中的n就不能是数组,因为prod(1:n)中已用了数 组[1:n]。这时必须用: • for k=1:6 x(k)=1/prod(1:k); end,x • 得 x = 1.0000 0.5000 0.1667 0.0417 0.0083 0.0014 • 在MATLAB中数列随n增加而变化的趋向很容易由 计算其数值并作图的方法来解决。但要求数列在n 趋向∞时的极限时往往要藉助于符号数学,可以 从下面的实例看出

【例5-3-1】 ·对下列各题的序列,问: 。 (①)。计算并画出其前25项,判断它是否收 敛。若收敛,极限L是多少? ()。如果序列收敛,找到数N,使得n>N后 的an都有a,-L≤0.01。如果要离极限L小 于0.0001,序列该取多长? (1)an=n,(2) (3)a,=sinn (4)
【例5-3-1】 • 对下列各题的序列,问: • (i)。计算并画出其前25项,判断它是否收 敛。若收敛,极限L是多少? • (ii)。如果序列收敛,找到数N,使得n>N后 的an都有 。如果要离极限L小 于0.0001,序列该取多长? (1) , (2) , (3) , (4) , 0.01 n a L − n n a n = 0.5 1 n n a n = + sin n a n = 1 sin n a n n =

解例5.3.1的程序 解:◆只要会写通项的表达式,程序是很简单的。 用数值计算方法时,四个题可编在一起如下: ·程序exn531 。n=1:25; 。a1=n.^(1./n) ·a2=(1+0.5./n).n; ·a3=sin(n); 。a4=n.*sin(1./n); plot(n,a1,n,a2,n,a3,n,a4)
解例5.3.1的程序 解:◆只要会写通项的表达式,程序是很简单的。 用数值计算方法时,四个题可编在一起如下: • 程序exn531 • n=1:25; • a1=n.^(1./n); • a2=(1+0.5./n).^n; • a3=sin(n); • a4=n.*sin(1./n); • plot(n,a1,n,a2,n,a3,n,a4)
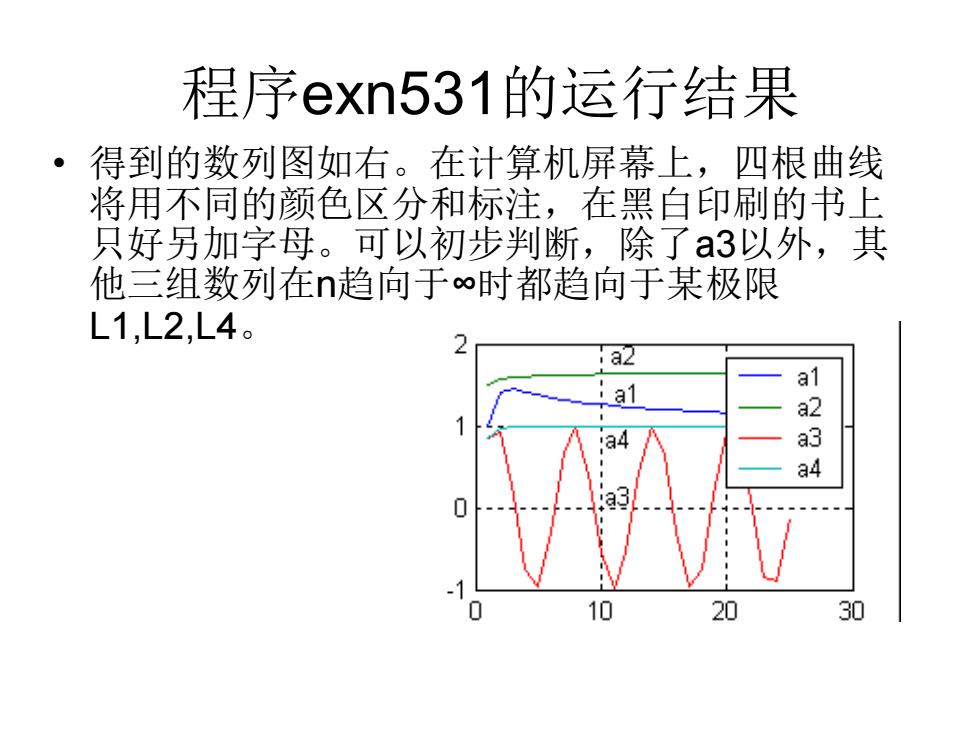
程序exn531的运行结果 ·得到的数列图如右。在计算机屏幕上,四根曲线 将用不同的颜色区分和标注,在黑白印刷的书上 只好另加字母。可以初步判断,除了a3以外,其 他三组数列在n趋向于∞时都趋向于某极限 L1,L2,L4。 2 a2 al 2 a4 a4 10 20 30
程序exn531的运行结果 • 得到的数列图如右。在计算机屏幕上,四根曲线 将用不同的颜色区分和标注,在黑白印刷的书上 只好另加字母。可以初步判断,除了a3以外,其 他三组数列在n趋向于∞时都趋向于某极限 L1,L2,L4

用符号数学求数列的极限 。 求极限最好用符号数学来解,主要的不同是自变 量应设为符号变量,所有的函数也要重写一次, 使它们也成为符号因变量,最好是在程序开始处 用clear命令清除掉前面程序在工作空间中生成的 同名数值变量。语句如下: 。clear,syms n .L1=limit(n^(1/n),inf) 。 %为了缩短语句,也可写成两句:a1=n(1n), L1=limit(n(1/n),inf) L2=limit((1+0.5./n).An,inf) L4=limit(n.*sin(1./n),inf) 。 程序运行后,得到L1=1,L2=e0(1/2),L4=1
用符号数学求数列的极限 • 求极限最好用符号数学来解,主要的不同是自变 量n应设为符号变量,所有的函数也要重写一次, 使它们也成为符号因变量,最好是在程序开始处 用clear命令清除掉前面程序在工作空间中生成的 同名数值变量。语句如下: • clear, syms n • L1= limit(n^(1/n),inf) • % 为了缩短语句,也可写成两句:a1= n^(1/n), L1= limit(n^(1/n),inf) • L2= limit((1+0.5./n).^n,inf) • L4= limit(n.*sin(1./n),inf) • 程序运行后,得到L1=1, L2=exp(1/2), L4=1

二.常数项级数 ● 无穷数列的累加称为级数,当取其前面若干有限 项时,得到的是部分和。将数列a累加形成的新序 列可用s=cumsum(a)实现,如果a的长度是n,则 s的长度也是n。即每一个s(k)是数组a中前k项的 和。注意cumsum与sum命令的区别,若 ss=sum(a),得到的是一个数,是序列 s=cumsum(a)中最后一项ss=s(n)。因为它是把a 中所有元素加在一起得到的最后结果。 。〉 MATLAB中同样有符号数学的累加命令,要注意 它与数值计算的差别,主要是符号数学没有数组 累加成数组的命令,只有求一个求总和的累加命 令symcum
二.常数项级数 • 无穷数列的累加称为级数,当取其前面若干有限 项时,得到的是部分和。将数列a累加形成的新序 列可用s=cumsum(a)实现,如果a的长度是n,则 s的长度也是n。即每一个s(k)是数组a中前k项的 和。注意cumsum与sum命令的区别,若 ss=sum(a),得到的是一个数,是序列 s=cumsum(a)中最后一项ss=s(n)。因为它是把a 中所有元素加在一起得到的最后结果。 • MATLAB中同样有符号数学的累加命令,要注意 它与数值计算的差别,主要是符号数学没有数组 累加成数组的命令,只有求一个求总和的累加命 令symcum

【例5-3-2】 ·设级数(a)&=立,(b>马,= n= n=1 n ·试观察它们的部分和序列变化的趋势,如果是收 敛的,计算出它们在趋向于无穷大时的极限值。 解:(1)。用数值方法计算的程序exn532如下: clear,n=input('n=);k=1:n; a1=1./k.^2;s1=cumsum(a1); a2=1./k;s2=cumsum(a2); plot(k,s1,k,s2),grid on s1(end),s2(end)
【例5-3-2】 • 设级数(a) ,(b) , • 试观察它们的部分和序列变化的趋势,如果是收 敛的,计算出它们在n趋向于无穷大时的极限值。 解:(1)。用数值方法计算的程序exn532如下: clear,n=input('n= ');k=1:n; a1=1./k.^2; s1=cumsum(a1); a2=1./k; s2=cumsum(a2); plot(k,s1,k,s2),grid on s1(end),s2(end) 1 2 1 1 , n s n = = 2 1 1 n s n = =

程序exn532的运行结果 ·键入n=20时,得到图形 如图,数值结果为: ·s1(end)= 1.59616324391302 3 …1…$2 ·s2(end)= 3.59773965714368 。 我们只能从图形上猜测 s1会趋向于一个极限, 而s2就难说了。 10 15 20
程序exn532的运行结果 • 键入n=20 时,得到图形 如图,数值结果为: • s1(end) = 1.59616324391302 • s2(end) = 3.59773965714368 • 我们只能从图形上猜测 s1会趋向于一个极限, 而s2就难说了