
5.4节数值积分和微分方程 数值解
5.4节 数值积分和微分方程 数值解

一.数值定积分求面积 ·【例5-4-1】用数值积分法求由y=-x2+115,y=0, =0与x10围成的图形面积,并讨论步长和积分方法对精 度的影响。 。分 解:◆原理用矩形法和梯形法分别求数值积分并作比较, 步长的变化用循环语句实现。MATLAB中的定积分有专门 的函数QUAD,QUADL等实现。为了弄清原理,我们先用 直接编程的方法来计算,然后再介绍定积分函数及其调用 方法。设x向量的长度取为n,即将积分区间分为n-1段, 各段长度为△x,(i=1,2,…,n-1)。算出各点的 y,(i=1,2,…,n+1),则矩形法数值积分公式为: ∑aAx
一.数值定积分求面积 • 【例5-4-1】 用数值积分法求由 ,y=0, x=0与x=10围成的图形面积,并讨论步长和积分方法对精 度的影响。 • 解: ◆原理 用矩形法和梯形法分别求数值积分并作比较, 步长的变化用循环语句实现。MATLAB中的定积分有专门 的函数QUAD,QUADL等实现。为了弄清原理,我们先用 直接编程的方法来计算,然后再介绍定积分函数及其调用 方法。设x向量的长度取为n,即将积分区间分为n-1段, 各段长度为 。算出各点的 ,则矩形法数值积分公式为: 2 y x = − +115 ( 1, 2, , 1) i = − x i n ( 1, 2, , 1) i y i n = + 1 1 n i i i s y x − = =

矩形和梯形定积分公式 。梯形法的公式为: 2 。 比较两个公式,它们之间的差别只是0.5(yn-)。 ·在MATLAB中,把向量中各元素叠加的命令是sum。把向 量中各元素按梯形法叠加的命令是trapz。梯形法的几何意 义是把被积分的函数的各计算点以直线相联,形成许多窄 长梯形条,然后叠加,我们把两种算法都编入同一个程序 进行比较
矩形和梯形定积分公式 • 梯形法的公式为: • 比较两个公式,它们之间的差别只是 。 • 在MATLAB中,把向量中各元素叠加的命令是sum。把向 量中各元素按梯形法叠加的命令是trapz。梯形法的几何意 义是把被积分的函数的各计算点以直线相联,形成许多窄 长梯形条,然后叠加,我们把两种算法都编入同一个程序 进行比较。 1 1 1 1 1 2 2 2 n n i i n i i i i i y y y y q x y x − − + = = + + = = + 0.5( y y n − 1 )

求面积的数值积分程序exn541 for dx=[2,1,0.5,0.1] %设不同步长 X=0:.1:10;y=-X.*x+115; %取较密的函数样本 plot(x,y),hold on %画出被积曲线并保持 x1=0:dx10;y1=-X1.*x1+115; %求取样点上的y1 %用矩形(欧拉)法求积分,注意末尾去掉一个点 n=length(x1);s=sum(y1(1:n-1))*dx; q=trapz(y1)*dx; %用梯形法求积分 stairs(x1,y1), %画出欧拉法的积分区域 plot(x1,y1) %画出梯形法的积分区域 [dx,s,q],pause(1) hold off,end
求面积的数值积分程序exn541 for dx=[2,1,0.5,0.1] % 设不同步长 x=0:.1:10;y=-x.*x+115; % 取较密的函数样本 plot(x,y),hold on % 画出被积曲线并保持 x1=0:dx:10;y1=-x1.*x1+115; % 求取样点上的y1 % 用矩形(欧拉)法求积分,注意末尾去掉一个点 n=length(x1);s=sum(y1(1:n-1))*dx; q=trapz(y1)*dx; % 用梯形法求积分 stairs(x1,y1), % 画出欧拉法的积分区域 plot(x1,y1) % 画出梯形法的积分区域 [dx,s,q],pause(1), hold off,end
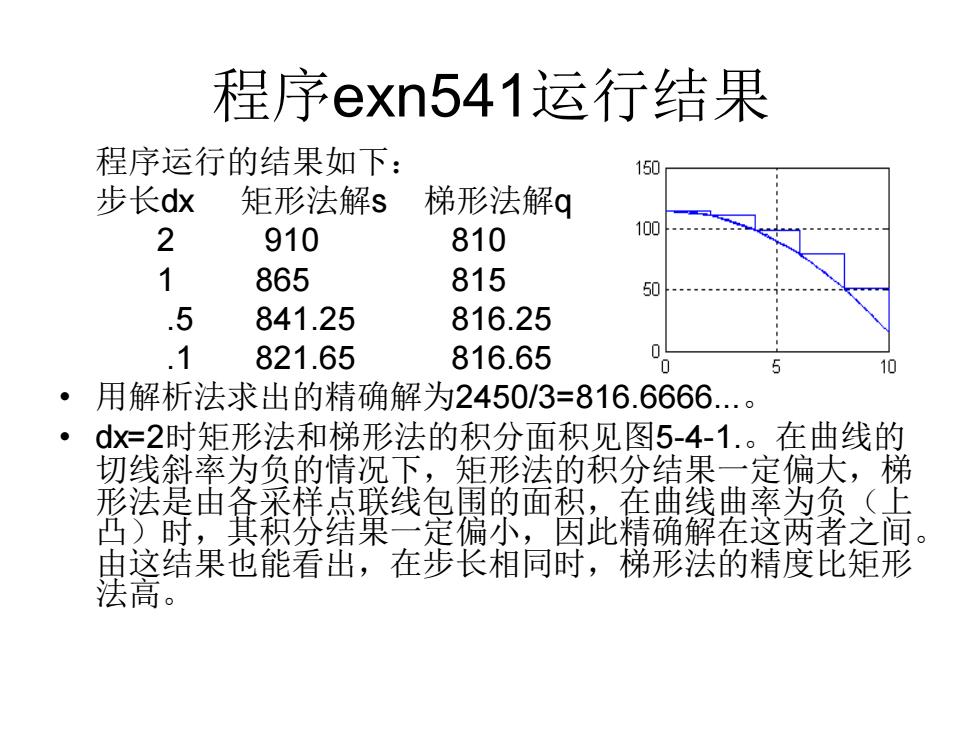
程序exn541运行结果 程序运行的结果如下: 150 步长dx 矩形法解s 梯形法解q 2 910 810 100 1 865 815 50 .5 841.25 816.25 .1 821.65 816.65 0 5 10 ·用解析法求出的精确解为2450/3=816.6666.。 dx2时矩形法和梯形法的积分面积见图5-4-1.。在曲线的 切线斜率为负的情况下,矩形法的积分结果一定偏大,梯 形法是由各采样点联线包围的面积,在曲线曲率为负(上 凸)时,其积分结菓一定偏小,因此精确解在这两者之间。 由这结果也能看出,在步长相同时,梯形法的精度比矩形 法高·
程序exn541运行结果 程序运行的结果如下: 步长dx 矩形法解s 梯形法解q 2 910 810 1 865 815 .5 841.25 816.25 .1 821.65 816.65 • 用解析法求出的精确解为2450/3=816.6666...。 • dx=2时矩形法和梯形法的积分面积见图5-4-1.。在曲线的 切线斜率为负的情况下,矩形法的积分结果一定偏大,梯 形法是由各采样点联线包围的面积,在曲线曲率为负(上 凸)时,其积分结果一定偏小,因此精确解在这两者之间。 由这结果也能看出,在步长相同时,梯形法的精度比矩形 法高

矩形法数字积分的演示程序rsums o MATLAB中有一个矩形法数 115-x.2:816.992188 字积分的演示程序rsums, 100 可以作一个对比。键入 rsums(115-x.2',0,10) 80 ·就得到右图。图中表示了被 60 积函数的曲线和被步长分割 的小区间,并按各区间中点 40 的函数值构成了各个窄矩形 面积。用鼠标拖动图下方的 20 滑尺可以改变步长的值,图 的上方显示的是这些矩形面 2 4 6 8 10 16 积叠加的结果
矩形法数字积分的演示程序rsums • MATLAB中有一个矩形法数 字积分的演示程序rsums, 可以作一个对比。键入 rsums('115-x.^2',0,10) • 就得到右图。图中表示了被 积函数的曲线和被步长分割 的小区间,并按各区间中点 的函数值构成了各个窄矩形 面积。用鼠标拖动图下方的 滑尺可以改变步长的值,图 的上方显示的是这些矩形面 积叠加的结果。 0 2 4 6 8 10 0 20 40 60 80 100 115-x.^2 : 816.992188 16

MATLAB内的数值定积分函数 ·在实际工作中,用MATLAB中的定积分求面积的 函数quad和quad可以得到比自编程序更高的精 度,因为quad函数用的是辛普生法,即把被和函 数用二次曲线逼近的算法,而quadli函数采用了更 高阶的逼近方法。它们的调用格式如下: Q=QUADL(FUN,A,B,TOL) 其中,FUN是表示被积函数的字符串,A是积分下 限,B是积分上限。TOL是规定计算的容差,其默 认值为1e-6 。1 例如,键入 S=quad('-X.*x+115',0,10) 得到 S=8.166666666666666e+002
MATLAB内的数值定积分函数 • 在实际工作中,用MATLAB中的定积分求面积的 函数quad和quadl可以得到比自编程序更高的精 度,因为quad函数用的是辛普生法,即把被积函 数用二次曲线逼近的算法,而quadl函数采用了更 高阶的逼近方法。它们的调用格式如下: Q = QUADL(FUN,A,B,TOL) 其中,FUN是表示被积函数的字符串, A是积分下 限,B是积分上限。TOL是规定计算的容差,其默 认值为1e-6 • 例如,键入 S = quad('-x.*x+115',0,10) 得到 S = 8.166666666666666e+002

二.求两条曲线所围图形的面积 【例5-4-2】。设f(x)=e-2os,g(x)=4c0s(x-2) 计算区间[0,4]上两曲线所围面积。 ·解:◆原理:先画出图形, .>dx=input('dx=;x=0:dx:4; ·>>f=eXp(-(x-2).2.*cos(pi*x)月 2 ·>>g=4*c0s(X-2): >plot(x,f,x,g,":r') 得到右图。从图上看到,其 中既有f(x)>g(的区域,也 有f(X)>g(X的区域
二.求两条曲线所围图形的面积 【例5-4-2】。设 计算区间[0,4]上两曲线所围面积。 • 解:◆原理:先画出图形, • >> dx=input('dx= ') ;x=0:dx:4; • >> f=exp(-(x-2).^2.*cos(pi*x)); • >> g=4*cos(x-2); • >> plot(x,f,x,g,':r') 2 ( 2) cos ( ) , ( ) 4cos( 2) x x f x e g x x − − = = − 得到右图。从图上看到,其 中既有f(x)>g(x)的区域,也 有f(x)>g(x)的区域

求两条曲线所围图形的面积() 若要求两曲线所围总面积(不管正负),则可加一条语句 >s=trapz(abs(f-g))*dx, 在dx=0.001时,得到s=6.47743996919702 若要求两曲线所围的f()>g()的正面积,则需要一定的技巧. ◆方法一。先求出交点x1,再规定积分上下限。 >>x1=fzero('exp(-(x-2).2.*c0s(pi*X)-4*cos(x-2)',1) %把积分限设定为0~x1,求出积分结果再乘以2: >>X=0:dxx1; >f=exp(-(x-2).^2.*cos(pi*x)); >>g=4*c0s(X-2); >s1=2*trapz(abs(f-g))*dx 在设定dx=0.001时,得到s1=2.30330486000857
求两条曲线所围图形的面积(1) 若要求两曲线所围总面积(不管正负),则可加一条语句 >> s=trapz(abs(f-g))*dx, 在dx=0.001时,得到s = 6.47743996919702 若要求两曲线所围的f(x)>g(x)的正面积,则需要一定的技巧. ◆方法一。先求出交点x1 ,再规定积分上下限。 >> x1=fzero('exp(-(x-2).^2.*cos(pi*x))-4*cos(x-2)',1) %把积分限设定为0~x1,求出积分结果再乘以2: >> x=0:dx:x1; >> f=exp(-(x-2).^2.*cos(pi*x)); >> g=4*cos(x-2); >> s1=2*trapz(abs(f-g))*dx 在设定dx=0.001时,得到s1 = 2.30330486000857

求两条曲线所围图形的面积(2) 方法二。调用MATLAB中求面积函数quad。这里的关键是建 立一个函数文件,把e1=f(x)-g(>0的部分取出来。 利用逻辑算式(e1>0),它在e1>0处取值为1,在e10)与e1作元素群乘法,正的e1将全 部保留,而负的e1就全部为零。因此编出子程序 exn542f.m如下: function e exn542f(x) ·e1=exp(-(x-2).2.*cos(pi*x)-4*cos(x-2); 。e=(e1>=0).*e1; 将它存入工作目录下。于是求此积分的主程序语句为: >>s2=quad('exn542f',0,4) ·得到的结果为: s2=2.30330244952618
求两条曲线所围图形的面积(2) 方法二。调用MATLAB中求面积函数quad。这里的关键是建 立一个函数文件,把e1=f(x)-g(x)>0的部分取出来。 • 利用逻辑算式(e1>0),它在e1>0处取值为1,在e10)与e1作元素群乘法,正的e1将全 部保留,而负的e1就全部为零。因此编出子程序 exn542f.m如下: • function e = exn542f(x) • e1=exp(-(x-2).^2.*cos(pi*x))- 4*cos(x-2); • e = (e1>=0).*e1; • 将它存入工作目录下。于是求此积分的主程序语句为: • >> s2=quad('exn542f',0,4) • 得到的结果为: • s2= 2.30330244952618