
第十章后续课矩阵建模举例
第十章 后续课矩阵建模举例
10.1多项式插值问题 例:试求三次插值多项式p)=a,+at+,r+a,r,使 曲线通过以下4个点:(0,3),(1,0),(2,-1),(3,6)。 解:这4个点的坐标应满足三次多项式函数,代入后有: a 100 a,+a1+a2+a3=0 111 a, a0+2a1+4a2 +8a3 =-1 124 8 a0+3a1+9a2+27a3=6 139272 6 程序: A=[1,0,0,0;1,1,1,1;1,2,4,8;1,3,9,27]; B=[3;0;-1;6];a=A\B 得到a=[3,-2,-2,1]T,即p(t)=3-2t-2t2+t
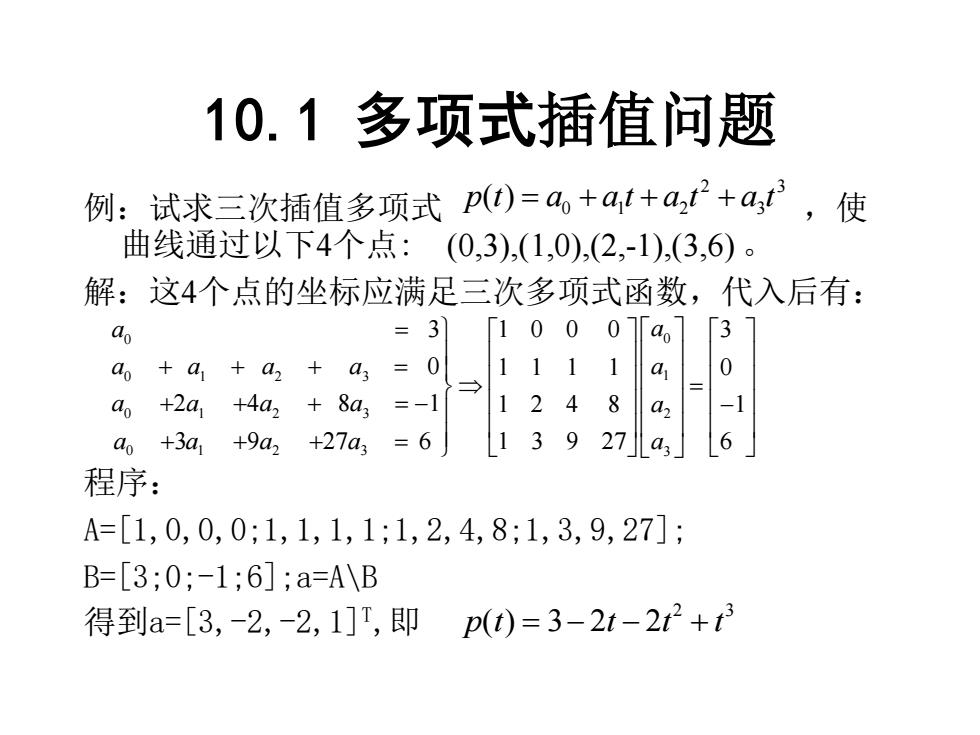
10.1 多项式插值问题 例:试求三次插值多项式 ,使 曲线通过以下4个点: (0,3),(1,0),(2,-1),(3,6) 。 解:这4个点的坐标应满足三次多项式函数,代入后有: 程序: A=[1,0,0,0;1,1,1,1;1,2,4,8;1,3,9,27]; B=[3;0;-1;6];a=A\B 得到a=[3,-2,-2,1]T ,即 2 3 0 1 2 3 p t a a t a t a t ( ) = + + + 0 0 0 1 2 3 1 0 1 2 3 2 0 1 2 3 3 3 1 0 0 0 3 0 1 1 1 1 0 2 4 8 1 1 2 4 8 1 3 9 27 6 1 3 9 27 6 a a a a a a a a a a a a a a a a a = + + + = = + + + = − − + + + = 2 3 p t t t t ( ) 3 2 2 = − − +
例10.1的图形 %绘图程序 ezp1ot('3-2*t-2*t^2+t^3') hold on,grid on 3-2t-2t2 p1ot([0:3],[3,0,-1,6],'x') 1ine([1.5,1.5],[0,6]) axis([-1,4,-2,8]) %求t=1.5处的插值函数值 t1=1.5: p1=3-2*t1-2*t1^2+t1^3 0 p1ot(t1,p1,'o') 图10.1例10.1的插值曲线
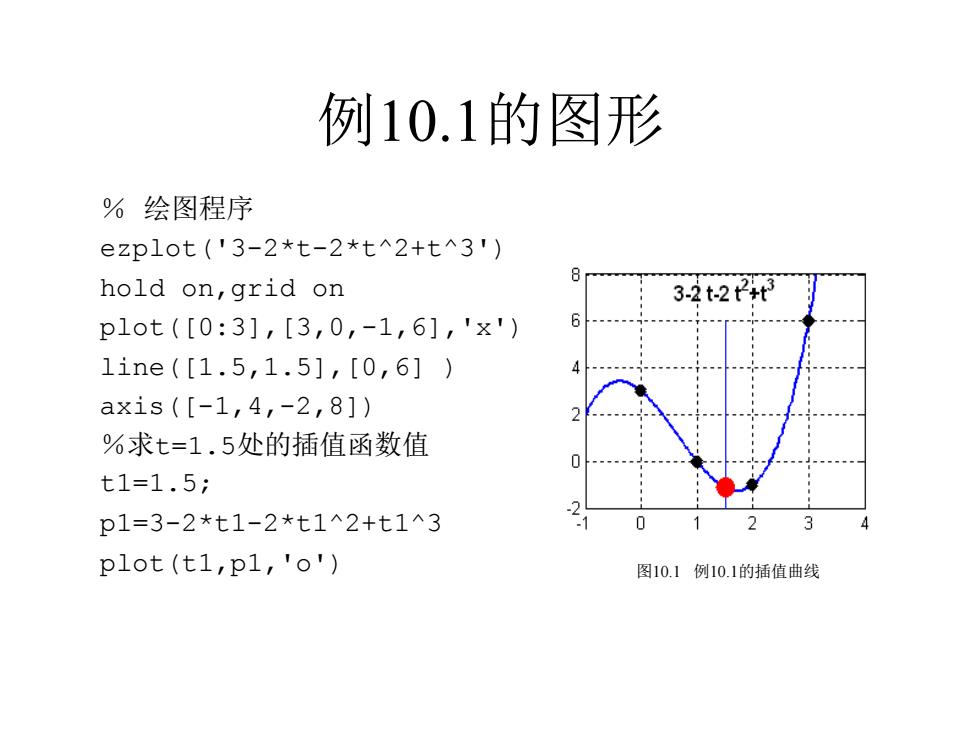
例10.1的图形 % 绘图程序 ezplot('3-2*t-2*t^2+t^3') hold on,grid on plot([0:3],[3,0,-1,6],'x') line([1.5,1.5],[0,6] ) axis([-1,4,-2,8]) %求t=1.5处的插值函数值 t1=1.5; p1=3-2*t1-2*t1^2+t1^3 plot(t1,p1,'o') 图10.1 例10.1的插值曲线

高阶的多项式插值 ·在一般情况下,当给出函数在+1个点上的值时,就可 以用n次多项式p(t)=a+a,t+a2t+…+a,t 对它进行插值。如果给出的点数(即方程数)大于+1, 方程组成为超定的,因而没有一个能满足方程组的解, 得出的曲线将是以最小二乘意义下的误差靠近各点, 于是插值就变为拟合。 ·插值也不一定是自变量的多项式,比如圆锥曲线方程 ax2+bxy+cy2+dx+ey+f=O 虽然它有6个系数,若用a除以此方程两端,得到的将 是有5个待定系数的方程。如果给出x-y平面上的5个点, 就可以列出5个线性方程来确定这5个系数
高阶的多项式插值 • 在一般情况下,当给出函数在n+1个点上的值时,就可 以用n次多项式 对它进行插值。如果给出的点数(即方程数)大于n+1, 方程组成为超定的,因而没有一个能满足方程组的解, 得出的曲线将是以最小二乘意义下的误差靠近各点, 于是插值就变为拟合。 • 插值也不一定是自变量的多项式,比如圆锥曲线方程 虽然它有6个系数,若用a除以此方程两端,得到的将 是有5个待定系数的方程。如果给出x-y平面上的5个点, 就可以列出5个线性方程来确定这5个系数。 2 2 ax bxy cy dx ey f + + + + + = 0 2 0 1 2 ( ) n n p t a a t a t a t = + + + +

10.2坐标测量仪测定的拟合 比如为了测量一个圆锥形截面的半径,可在x-y 平面内测量其圆周上n个点的坐标(x:,y:) (i=1,..n),然后拟合出此截面的方程。 ●〉 对于每一组数据(x,y),代入圆锥曲线方程, 移项可得: xy9+yc2+x,C3+y,c4+C5=-x;2(i=1,2,…,n) n个点就有n个方程。其结构相同,只是数据 不同。可以把数据写成列向量,然后用元素群 运算一次列出所有的n个方程
10.2 坐标测量仪测定的拟合 • 比如为了测量一个圆锥形截面的半径,可在x-y 平面内测量其圆周上n个点的坐标(xi,yi) (i=1,…n),然后拟合出此截面的方程。 • 对于每一组数据(xi ,yi),代入圆锥曲线方程, 移项可得: n个点就有n个方程。其结构相同,只是数据 不同。可以把数据写成列向量,然后用元素群 运算一次列出所有的n个方程。 2 2 1 2 3 4 5 ( 1,2, , ) i i i i i i x y c y c x c y c c x i n + + + + = − =

例10.2圆锥截面方程的拟合 设测量了圆周上7个点,其x,y坐标如下: x=-3.000 -2.000-1.00001.000 2.0003.000 y=3.03 3.90 4.354.504.404.02 3.26 试求出此圆锥截面的方程,并求其最大最小直径。 列出程序如下: x=[-3:3]'; 号把x,y赋值为列向量 y=[3.03,3.90,4.35,4.50,4.40,4.02,3.26]': A=[x.*y,y.*y,x,y,ones (size(x))]B=-x.^2; 号列出系数矩阵A和B c=inv(A'*A)*A'*B, 号解超定方程得出c
例10.2 圆锥截面方程的拟合 设测量了圆周上7个点,其x,y坐标如下: x = -3.000 -2.000 -1.000 0 1.000 2.000 3.000 y= 3.03 3.90 4.35 4.50 4.40 4.02 3.26 试求出此圆锥截面的方程,并求其最大最小直径。 列出程序如下: x=[-3:3]'; % 把x,y赋值为列向量 y=[3.03,3.90,4.35,4.50,4.40,4.02,3.26]'; A=[x.*y, y.*y, x, y, ones(size(x))]; B=-x.^2; % 列出系数矩阵A和B c=inv(A'*A)*A'*B, % 解超定方程得出c
程序运行结果 ·将程序运行生成的参数写出,应为: -9.09009.1809-3.0000 3.0300 9 -7.800015.2100 -2.0000 3.9000 -4 0.0050 -4.350018.9225 -1.0000 4.3500 1 0.9214 A= 0 20.2500 0 4.5000 1 B= 0 C= -0.2228 4.400019.36001.0000 4.4000 -1 -0.4050 8.040016.16042.0000 4.0200 1 -4 -16.8537 9.780010.62763.0000 3.2600 -9 ·即截面的方程为: x2+0.0050xy+0.9214y2-0.2228x-0.4050y-16.8537=0
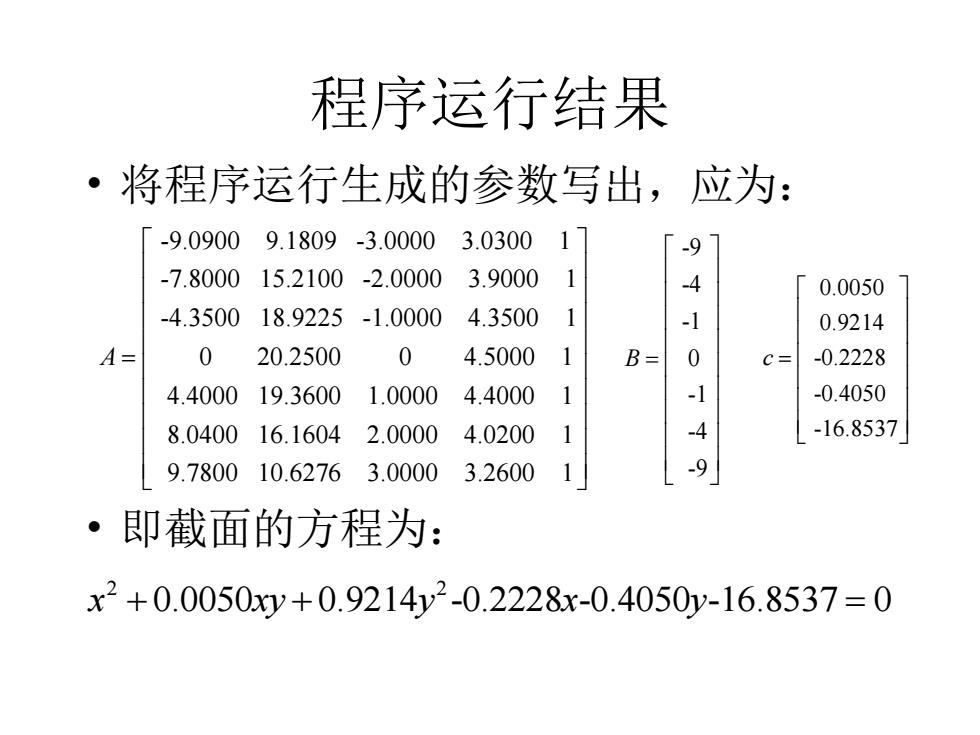
程序运行结果 • 将程序运行生成的参数写出,应为: • 即截面的方程为: -9.0900 9.1809 -3.0000 3.0300 1 -7.8000 15.2100 -2.0000 3.9000 1 -4.3500 18.9225 -1.0000 4.3500 1 0 20.2500 0 4.5000 1 4.4000 19.3600 A = 1.0000 4.4000 1 8.0400 16.1604 2.0000 4.0200 1 9.7800 10.6276 3.0000 3.2600 1 -9 -4 -1 0 -1 -4 -9 B = 0.0050 0.9214 -0.2228 -0.4050 -16.8537 c = 2 2 x xy y x y + + = 0.0050 0.9214 -0.2228 -0.4050 -16.8537 0

例10.2曲线 ezplot(x2+0.005*x*y+0.9214*y2-0.2228*x-0.4050*y-16.8537) % 画圆锥曲线 hold on,plot(x,y,'x') %画测量点 grid on,axis equal %x,y两方向取同样比例尺 拟合的图形和给定的测量点, 如图所示。从工程角度看, 0 这样的测量点布局对拟合 精度不大有利。 X+0.005xy+0.9214y 0.22280.4050y-16537=0
例10.2 曲线 ezplot('x^2+0.005*x*y+0.9214*y^2-0.2228*x-0.4050*y-16.8537') % 画圆锥曲线 hold on, plot(x,y,'x') % 画测量点 • grid on, axis equal % x,y两方向取同样比例尺 拟合的图形和给定的测量点, 如图所示。从工程角度看, 这样的测量点布局对拟合 精度不大有利

估计圆直径的方法 ·设圆周方程为: (x-C)2+y-C2)2=r2 C1,c2为圆心的坐标,为半径。整理上述方程,得到 2xC,+2yC2+(r2-C2-c22)=2xC+2yC2+C3=x2+y2 用n个测量点坐标(x,y)代入,得到 2x21 2+2 2X2 2y2 →Ac=B ·这是关于三个未知数的个线性方程,所以是一个超定 问题。解出就可得知这个最小二乘圆的圆心坐标和半 径r的值: r=vc;+c2+c
估计圆直径的方法 • 设圆周方程为: c1 ,c2为圆心的坐标,r为半径。整理上述方程,得到 • 用n个测量点坐标(xi,yi)代入,得到 • 这是关于三个未知数的n个线性方程,所以是一个超定 问题。解出就可得知这个最小二乘圆的圆心坐标和半 径r的值: 2 2 2 1 2 ( ) ( ) x c y c r − + − = 2 2 2 2 2 2 2 ( ) 2 2 1 2 1 2 1 2 3 xc yc r c c xc yc c x y + + − − = + + = + 2 2 1 1 1 1 1 2 2 2 2 2 2 2 3 2 2 2 2 1 2 2 1 2 2 1 n n n n x y x y c x y x y c c x y x y + + = + Ac = B 2 2 3 1 2 r c c c = + +

例10.2a曲线程序及运行结果 程序ag1002a x=[-3:3]'; 号把x,y赋值为列向量 y=[3.03,3.90,4.35,4.50,4.40,4.02,3.26]': A=[2*x,2*y,ones(size(x))]号求出系数矩阵A,B B=X.^2+y.^2 c=inv (A'*A)*A'*B, 号求超定方程的解,得出c r=sqrt(c(3)+C(1)^2+c(2)^2) 号由c求出r 程序运行的最后结果为: c=0.1018 工件圆心的x坐标 0.4996 工件圆心的y坐标 15.7533 r= 4.0017 工件的半径r
例10.2a 曲线程序及运行结果 程序ag1002a x=[-3:3]'; % 把x,y赋值为列向量 y=[3.03,3.90,4.35,4.50,4.40,4.02,3.26]'; A=[2*x, 2*y, ones(size(x))] % 求出系数矩阵A,B B=x.^2+y.^2 c=inv(A'*A)*A'*B, % 求超定方程的解,得出c r=sqrt(c(3)+c(1)^2+c(2)^2) % 由c求出r 程序运行的最后结果为: c = 0.1018 工件圆心的x坐标 0.4996 工件圆心的y坐标 15.7533 r = 4.0017 工件的半径r