
用主元连乘法定义行列式 工科线性代数现代化和大众化的思路之二 西安电子科技大学陈怀琛高淑萍 email:hchchen1934@vip.163.com 清要:提出了用主元连乘积法来定义行列式,可以把高斯消元法与行列式有机地联系起来,大大简化 行列式的理论讲授难度,可以避开的许多困惑的概念,并且使行列式的计算和编程十分方便快捷。这 从1995到2004的十年间,为了把科学计算软件用于机械、电子、控制等类工科课程, 我写了五本书,涉及十多门课程,解了超百道的线性代数问题,直正体验了后续课程和工程 问题对线性代数的需要。发现工科线性代数现代化和大众化的首要手段是引进机算。其次 许多老师根本不知道工程上是如何应用线性代数的,凭想象选材。造成在内容上,“有用的 不教,教了的没用”。本文只就行列式的用法和算法问题做些探讨。 一、 工科后续课究竟如何用行列式的? 工学生遇到的主要线性代数问颗是解方得组,其阶数常为五阶以上,直到成百上千 求解的基本原理是高斯消元法,采用的工具是计算机,用手工笔算是不可能的。不过现在的 大学数学就是偏偏只教笔算,只管解三阶以下的题目。“不教机算”的问题我己谈得很多 20O9年高教司己立项“用MATLAB和建模实践改造工科线性代数”来解决这个问题,有 19所大学,45000名学生参与了试点,深受师生欢迎,现在正在继续推广,本文就不多说了。 在这里我要谈的是线性代数中的一个困难的理论问题一一行列式,应该如何教。 大家知道,“行列式不为零”是判断线性方程组解存在的根据,从数学上看,必不可 因此现在的线性代数老师教给学生的是这样一个概念:拿米一个线性方程组,先算它的系数 行列式,如果它不等于零,再去求解:否则就不算了。实际情况远非如此,我解的上百道矩 阵应用恩目,都是直接求解方程,没有先算行列式“判解”这个步骤。其原因何在呢? 1.先判解,后求解,这样的操作顺序要有一个前提,那就是,判解应该比求解容易」 如果求解快,判解慢,那有何必多此一举去“判解”呢?因此,计算复杂度是关键,当前线 性代数中不考虑计算复杂度是一个大的缺陷。 2.方程组求解现在都用高斯消元法,数学上早有证明,那是最快的方法。行列式的计 算法则随定义而定,现有三种定义方法[:显式法、代数余子式法和主元连乘积法。我国 的现有教材从来都不讲第三种,而前两种定义下的计算复杂度极高。三阶及以上的系统,判 解远慢于求解。阶数愈高,两者的差距愈大。因此,判解实际上是不进行的。 3.消元法求解 的过程中,已经经历 解的存在性的 判断 只要 消元所 的行阶梯矩阵 的主对角线上的元素不为零,方程组就有解:主元出现零,方程就无解。其实,求出了行阶 梯矩阵,用主元连乘积的定义,己经可以很方使地通过N1次连乘,得到行列式的值,所 以求解和求行列式几乎是同时完成的,并不需要多付出双倍以至千百倍的无用功来先判解 的。尤其是使用计算机解题时,如果出现了某个零主元,计算机会发出出错告警,指出系数 行列式接近或等于于零。 二、 用主元连乘积法定义行列式
1 用主元连乘法定义行列式 ——工科线性代数现代化和大众化的思路之二 西安电子科技大学 陈怀琛 高淑萍 email: hchchen1934@vip.163.com 摘要:提出了用主元连乘积法来定义行列式,可以把高斯消元法与行列式有机地联系起来,大大简化 行列式的理论讲授难度,可以避开的许多困惑的概念,并且使行列式的计算和编程十分方便快捷。这 从 1995 到 2004 的十年间,为了把科学计算软件用于机械、电子、控制等类工科课程, 我写了五本书,涉及十多门课程,解了超百道的线性代数问题,真正体验了后续课程和工程 问题对线性代数的需要。发现工科线性代数现代化和大众化的首要手段是引进机算。其次, 许多老师根本不知道工程上是如何应用线性代数的,凭想象选材。造成在内容上,“有用的 不教,教了的没用”。本文只就行列式的用法和算法问题做些探讨。 一、 工科后续课究竟如何用行列式的? 工科学生遇到的主要线性代数问题是解方程组。其阶数通常为五阶以上,直到成百上千。 求解的基本原理是高斯消元法,采用的工具是计算机,用手工笔算是不可能的。不过现在的 大学数学就是偏偏只教笔算,只管解三阶以下的题目。“不教机算”的问题我已谈得很多, 2009 年高教司已立项“用 MATLAB 和建模实践改造工科线性代数”来解决这个问题,有 19 所大学,45000 名学生参与了试点,深受师生欢迎,现在正在继续推广,本文就不多说了。 在这里我要谈的是线性代数中的一个困难的理论问题——行列式,应该如何教。 大家知道,“行列式不为零”是判断线性方程组解存在的根据,从数学上看,必不可少。 因此现在的线性代数老师教给学生的是这样一个概念:拿来一个线性方程组,先算它的系数 行列式,如果它不等于零,再去求解;否则就不算了。实际情况远非如此,我解的上百道矩 阵应用题目,都是直接求解方程,没有先算行列式“判解”这个步骤。其原因何在呢? 1. 先判解,后求解,这样的操作顺序要有一个前提,那就是,判解应该比求解容易。 如果求解快,判解慢,那有何必多此一举去“判解”呢?因此,计算复杂度是关键,当前线 性代数中不考虑计算复杂度是一个大的缺陷。 2. 方程组求解现在都用高斯消元法,数学上早有证明,那是最快的方法。行列式的计 算法则随定义而定,现有三种定义方法[1]:显式法、代数余子式法和主元连乘积法。我国 的现有教材从来都不讲第三种,而前两种定义下的计算复杂度极高。三阶及以上的系统,判 解远慢于求解。阶数愈高,两者的差距愈大。因此,判解实际上是不进行的。 3. 消元法求解的过程中,已经经历了解的存在性的判断。只要消元所得的行阶梯矩阵 的主对角线上的元素不为零,方程组就有解;主元出现零,方程就无解。其实,求出了行阶 梯矩阵,用主元连乘积的定义,已经可以很方便地通过 N-1 次连乘,得到行列式的值,所 以求解和求行列式几乎是同时完成的,并不需要多付出双倍以至千百倍的无用功来先判解 的。尤其是使用计算机解题时,如果出现了某个零主元,计算机会发出出错告警,指出系数 行列式接近或等于于零。 二、 用主元连乘积法定义行列式

1.设二阶方阵开始,设二阶方阵的系数矩阵为A口],只用第三类初等变换来 c d 消元。所得的行阶梯矩阵为:U=厂口,6 0 d-b*cla ,对角项(主元)的连乘积D不为零, 得到 D=ad-bc0 这个D=ad-bc就称为矩阵A的行列式。 可见,二阶线性方程组主元的连乘积就等于行列式。如果用矩阵的下标来标注元素, 其行列式为D-a,a2a1a21 2..三阶方程组的行列式 设三阶方程组的系数矩阵为 A=azazaz [a3 an a 则只用第三类初等变换的高斯消元法求得其上三角矩阵如下: ap U=0 (ana-2aa)/an a-aaa 00(a1anagtaagd31ta1a2aa1gana1ana2ra9aaxg0n/(aanaza2i月 要求三个对角元素的连乘积不为零。结果为: anan a D=4u4242g=a44g+aag41+ag402-44a41-a44g-a4s42≠0 可见用主元连乘积也同样可定义三阶系数矩阵的行列式·为了使行列式的值具有唯一 性,必须限定消元变换中不使用第 一类(会改变正负号)和第二类(会改变乘数)初等变换 3.向高阶行列式的演绎 由此可以推想,将N阶系数方阵用高斯消元法变 换为上三角方阵,其对角线上所有主元的连乘积就是 「乃1*…** 该方阵的行列式,即D=BP2…Pm。我们已经知 U= 0P2…*◆ ……… 道,消元法解方程时,若主元不等于零,解就存在并 可用除法求得。所以,在这个定义下,判断行列式是 L000Pm:*」 否为零与判断诸主元是否为零是等价的。反过来说,用消元法如能求出方程组的解,则此方 程组系数矩阵的主元,因而行列式必不等于零,再用行列式去判解是多此一举。 许多数学书上对此定义方法早有定论。比如在中明确地 指出主元连乘积法是现有的 行列式的三种定义方法之一。不知什么原因,得不到重视。中国直到2012年游宏教授的教 材2]中才首次见到其推导证明。 三、 高阶行列式的三种定义方法
2 1.设二阶方阵开始,设二阶方阵的系数矩阵为 a b c d = A ,只用第三类初等变换来 消元,所得的行阶梯矩阵为: 0 - * / a b d b c a = U ,对角项(主元)的连乘积 D 不为零, 得到 D=ad-bc≠0 这个 D=ad-bc 就称为矩阵 A 的行列式。 可见,二阶线性方程组主元的连乘积就等于行列式。 如果用矩阵的下标来标注元素, 其行列式为 D=a a -a a 11 22 12 21 。 2..三阶方程组的行列式 设三阶方程组的系数矩阵为 11 12 13 21 22 23 31 32 33 a a a a a a a a a = A 则只用第三类初等变换的高斯消元法求得其上三角矩阵如下: ( ) ( ) 11 12 13 11 22 12 21 11 23 13 21 11 11 22 33 12 23 31 13 21 32 13 22 31 12 21 33 11 23 32 11 22 12 21 a a a 0 a a -a a /a a -a a /a 0 0 (a a a +a a a +a a a -a a a -a a a -a a a )/ a a -a a = U 要求三个对角元素的连乘积不为零。结果为: 11 12 13 21 22 23 11 22 33 12 23 31 13 21 32 13 22 31 12 21 33 11 23 32 31 32 33 0 a a a D a a a a a a a a a a a a a a a a a a a a a a a a = = + + − − − 可见用主元连乘积也同样可定义三阶系数矩阵的行列式。为了使行列式的值具有唯一 性,必须限定消元变换中不使用第一类(会改变正负号)和第二类(会改变乘数)初等变换。 3. 向高阶行列式的演绎 由此可以推想,将 N 阶系数方阵用高斯消元法变 换为上三角方阵,其对角线上所有主元的连乘积就是 该方阵的行列式,即 D p p p = 11 22 nn 。我们已经知 道,消元法解方程时,若主元不等于零,解就存在并 可用除法求得。所以,在这个定义下,判断行列式是 否为零与判断诸主元是否为零是等价的。反过来说,用消元法如能求出方程组的解,则此方 程组系数矩阵的主元,因而行列式必不等于零,再用行列式去判解是多此一举。 许多数学书上对此定义方法早有定论。比如在[1]中明确地指出主元连乘积法是现有的 行列式的三种定义方法之一。不知什么原因,得不到重视。中国直到 2012 年游宏教授的教 材[2]中才首次见到其推导证明。 三、 高阶行列式的三种定义方法 11 22 0 * 0 0 0 nn p p p = U
可以认为三种高阶行列式定义方法都是从二、三阶行列式从形式上向上演绎而得出的。 显式法是从各元素下标的排列组合规律向上演绎,代数余子式法是从矩阵按行展开的规则进 行演绎,而主元连乘积法则是从消元法所得上三角矩阵向上演绎的 1.显式法:按照这个定义,n×n矩阵的行列式中每一项将由不同行不同列的n个矩阵 元素乘积组成(即要做!次乘法),这些项应该能覆盖所有可能的排列方式,根据排列理论 行列式将有N=nl项相加。即使n=10,N将达3628800,而需要的乘法次数为n×(m-1)1之多, 而每顶的正负号将由这项下标排列的逆序者决定,还需要更多的计算量。所以思式法也私 为‘大公式”法 显式法中的逆序和列计数对非数学系的大学新生往往是拦路虎。而它的 运算量 仅超越 人们笔算可能性 也超越了计算机的能力 个25阶 的行列式若按这 大公式来算,用每秒1万亿次的超级计算机,也要算1200万年才能得出结果。这种现象在 计算数学上称为“维数灾难”。所以它的主要用途是数学推理,搞数学的当然不可缺少,但 在应用上并没有多少价值。 之代煮金子式法男路是格心在的行列试化达个X蚊的 (考虑正负号后称为代数 子式) 的线性组 可以减少高阶行列 逐级综合,就可由-1阶行列式向上定义阶行列式。因为二阶行列式要两次乘法,按照 个方法,三阶行列式要三个二阶行列式的线性组合,即要3升3*2=9次乘法,四阶行列式要 4+4*9=40次乘法,…依此类推,当n很大时,要算的是nl个二阶行列式的线性组合,近似 为2m次乘法。因此,这种方法的计算量与显式法相差不大,其主要好处是可以避开逆序定 义和排列组合理论,但不可能成为有实用计算价值的方法。 3.主元连乘法 它的核心是高斯消元法,通过等价变换消元,将系数矩阵化为上三角 阵,然后把主对角线上n个主元连乘:得到行列式。这种定义的运算量己经在消元法中讨论 过,实现上三角矩阵所需的计算量约为Nn3,n=10时,N-333次,n=25时,Ns5200, 用现有的微机可以在微秒级的时间内完成。求行列式只要做一个n元的连乘,其运算量可忽 略不计。它的另一个好处是把方程组求解和求系数行列式在同一个运算过程用同一个程序来 也就是把判解(的存在 一性)和求解统 一起来,实际上所有数学软件计算行列式 都采用这种方法。用MAAB为例,只用两条语句: [L.Ulu(A): %对方阵A做LU分解 D=prod(diag(U)%U的主对角线元素连乘积即为A的行列式 行列式的三种定义方法所需乘法次数列表如下 阶数N 23 5 10 25 高斯消元法求主元N3 31121 41 333 5208 消元法求行列式N3+N-141324 342 5233 代数余子式法求行列式≈2N!29 057257600 .1022e+025 显式法求行列式N1)N2 480 326592003.7227e+026 从此表可以看出,只有N=2时,用显式法判解才比消元法方便。=3时,两者的计算 基本相同。>3时,N每加一,用显式法定义的计算量成十倍地增长。代数余子式法计算量 与显式法基本相同,只有消元法的计算量最小,而且不引进其他新概念,理应作为高阶行列 式计算的首选。对于非数学类的学生 应该教他们走 条比 平坦好走的路走到目标,没必 要选一条难走的悬崖峭壁让大家去攀爬,因而又得去学习各种攀登的技巧和工具,人为地给 咪程增加了难度。 四、 行列式性质教法的改变 采用主元连乘法讲行列式后,逆序数、排列组合,代数余子式、矩阵按行展开,件随矩 阵等许多概 可以 那样是不是会影响 理解行列式的性质呢?初步的探索证明 3
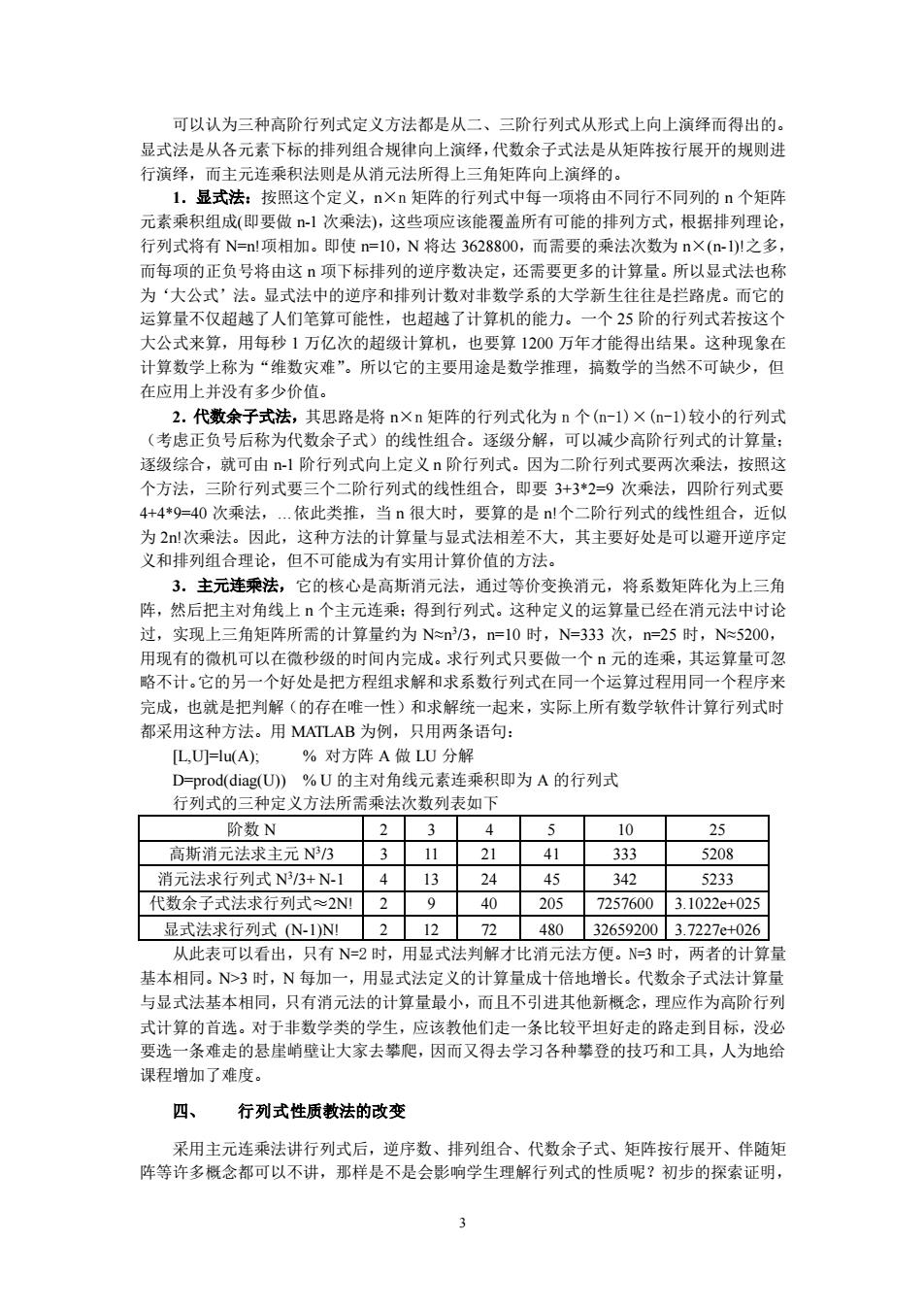
3 可以认为三种高阶行列式定义方法都是从二、三阶行列式从形式上向上演绎而得出的。 显式法是从各元素下标的排列组合规律向上演绎,代数余子式法是从矩阵按行展开的规则进 行演绎,而主元连乘积法则是从消元法所得上三角矩阵向上演绎的。 1.显式法:按照这个定义,n×n 矩阵的行列式中每一项将由不同行不同列的 n 个矩阵 元素乘积组成(即要做 n-1 次乘法),这些项应该能覆盖所有可能的排列方式,根据排列理论, 行列式将有 N=n!项相加。即使 n=10,N 将达 3628800,而需要的乘法次数为 n×(n-1)!之多, 而每项的正负号将由这 n 项下标排列的逆序数决定,还需要更多的计算量。所以显式法也称 为‘大公式’法。显式法中的逆序和排列计数对非数学系的大学新生往往是拦路虎。而它的 运算量不仅超越了人们笔算可能性,也超越了计算机的能力。一个 25 阶的行列式若按这个 大公式来算,用每秒 1 万亿次的超级计算机,也要算 1200 万年才能得出结果。这种现象在 计算数学上称为“维数灾难”。所以它的主要用途是数学推理,搞数学的当然不可缺少,但 在应用上并没有多少价值。 2.代数余子式法,其思路是将 n×n 矩阵的行列式化为 n 个(n-1)×(n-1)较小的行列式 (考虑正负号后称为代数余子式)的线性组合。逐级分解,可以减少高阶行列式的计算量; 逐级综合,就可由 n-1 阶行列式向上定义 n 阶行列式。因为二阶行列式要两次乘法,按照这 个方法,三阶行列式要三个二阶行列式的线性组合,即要 3+3*2=9 次乘法,四阶行列式要 4+4*9=40 次乘法,…依此类推,当 n 很大时,要算的是 n!个二阶行列式的线性组合,近似 为 2n!次乘法。因此,这种方法的计算量与显式法相差不大,其主要好处是可以避开逆序定 义和排列组合理论,但不可能成为有实用计算价值的方法。 3.主元连乘法,它的核心是高斯消元法,通过等价变换消元,将系数矩阵化为上三角 阵,然后把主对角线上 n 个主元连乘;得到行列式。这种定义的运算量已经在消元法中讨论 过,实现上三角矩阵所需的计算量约为 N≈n 3 /3,n=10 时,N=333 次,n=25 时,N≈5200, 用现有的微机可以在微秒级的时间内完成。求行列式只要做一个 n 元的连乘,其运算量可忽 略不计。它的另一个好处是把方程组求解和求系数行列式在同一个运算过程用同一个程序来 完成,也就是把判解(的存在唯一性)和求解统一起来,实际上所有数学软件计算行列式时 都采用这种方法。用 MATLAB 为例,只用两条语句: [L,U]=lu(A); % 对方阵 A 做 LU 分解 D=prod(diag(U)) % U 的主对角线元素连乘积即为 A 的行列式 行列式的三种定义方法所需乘法次数列表如下 阶数 N 2 3 4 5 10 25 高斯消元法求主元 N3 /3 3 11 21 41 333 5208 消元法求行列式 N3 /3+ N-1 4 13 24 45 342 5233 代数余子式法求行列式≈2N! 2 9 40 205 7257600 3.1022e+025 显式法求行列式 (N-1)N! 2 12 72 480 32659200 3.7227e+026 从此表可以看出,只有 N=2 时,用显式法判解才比消元法方便。N=3 时,两者的计算量 基本相同。N>3 时,N 每加一,用显式法定义的计算量成十倍地增长。代数余子式法计算量 与显式法基本相同,只有消元法的计算量最小,而且不引进其他新概念,理应作为高阶行列 式计算的首选。对于非数学类的学生,应该教他们走一条比较平坦好走的路走到目标,没必 要选一条难走的悬崖峭壁让大家去攀爬,因而又得去学习各种攀登的技巧和工具,人为地给 课程增加了难度。 四、 行列式性质教法的改变 采用主元连乘法讲行列式后,逆序数、排列组合、代数余子式、矩阵按行展开、伴随矩 阵等许多概念都可以不讲,那样是不是会影响学生理解行列式的性质呢?初步的探索证明

比较容易用主元连乘法定义证明的性质有下面一些: 任意三角方阵、对角方阵的行列式等于其对角元素的连乘积: 类初等矩阵的行列式分别为1k和1: *从A的某行中加上另一行的倍数,其行列式不变: *方阵中任意山两行交换,行列式反号: 方阵中若有一个全零行,其行列式为零 如果A中两行的元素相同或差同样倍数,行列式等于零 *如果A奇异,则dtA0,如果A可逆,则detA0,这已在行列式定义中证明 *方阵A与它的转置AT的行列式相等。即A=AT|。 也有一些性质则不易用主元连乘法证明,比如行列式按行展开等。哪些性质对学生重要, 关键是题研究这些性质对学生未来工作有什么应用价值。行列式按行展开的作用是便于相 理,这对数学系必不可 另个作用是为高阶行列式的手工计算服 根据前面的 析,它并不能减 少多少复杂度。对于工科学生,在采用主元连乘法和计算机软件来算行列式 后,这类用处不大的性质,是可以不讲的。 五、 结论 高等教有的现代化和大众化是现代社会发展的需要,大学数学向真实世界数学靠拢是它 改革的基本目 科线性代数的大众化改革是养 有潜力的[3)。把行列式与消元法无缝连 接可以大大减轻课程的难度并提高它的实践性,也提高了课程的内在逻辑性。老师可以把讲 课的重点放在行列式的几何及物理意义上,无需花很多时间去讲它的性质与计算,其优点是 无可比拟的。至于采取了这种讲法,原来为显式法或代数余子式法准备的那些概念应该怎样 外理?哪些保留?哪些扬弃?背定是一个极有角论性的问。因为各个专业、各类学生的要 求都会不同,传统的考研命 各个学校、专业和各类学生也都该有不同 的方式,这些只能留给大家在实践中去百花齐放 参考文歌 Introduction to Linear Algebra 4th Editin.ilsley-Cambridge Press.2009,p.24 [陈论 科线性
4 比较容易用主元连乘法定义证明的性质有下面一些: *任意三角方阵、对角方阵的行列式等于其对角元素的连乘积; *第一、二、三类初等矩阵的行列式分别为-1,k 和 1; *从 A 的某行中加上另一行的倍数,其行列式不变; *方阵中任意 i,j 两行交换,行列式反号; *方阵中若有一个全零行,其行列式为零。 *如果 A 中两行的元素相同或差同样倍数,行列式等于零。 *如果 A 奇异,则 det A=0,如果 A 可逆,则 det A≠0,这已在行列式定义中证明。 *方阵 A 与它的转置 AT的行列式相等。即 T A A = 。 也有一些性质则不易用主元连乘法证明,比如行列式按行展开等。哪些性质对学生重要, 关键是要研究这些性质对学生未来工作有什么应用价值。行列式按行展开的作用是便于推 理,这对数学系必不可少,另一个作用是为高阶行列式的手工计算服务,其实根据前面的分 析,它并不能减少多少复杂度。对于工科学生,在采用主元连乘法和计算机软件来算行列式 后,这类用处不大的性质,是可以不讲的。 五、 结论 高等教育的现代化和大众化是现代社会发展的需要,大学数学向真实世界数学靠拢是它 改革的基本目标,工科线性代数的大众化改革是很有潜力的[3]。把行列式与消元法无缝连 接可以大大减轻课程的难度并提高它的实践性,也提高了课程的内在逻辑性。老师可以把讲 课的重点放在行列式的几何及物理意义上,无需花很多时间去讲它的性质与计算,其优点是 无可比拟的。至于采取了这种讲法,原来为显式法或代数余子式法准备的那些概念应该怎样 处理?哪些保留?哪些扬弃?肯定是一个极有争论性的问题。因为各个专业、各类学生的要 求都会不同,传统的考研命题也会继续产生影响。各个学校、专业和各类学生也都该有不同 的方式,这些只能留给大家在实践中去百花齐放了! 参考文献 [1] Gilbert Strang, Introduction to Linear Algebra, 4th Edition, Wilsley-Cambridge Press, 2009, pp.244 [2] 游宏,朱广俊,线性代数,北京,高等教育出版社,2012 年3 月 [3] 陈怀琛,论工科线性代数的现代化与大众化,高等数学研究,第 15 卷,第 2 期,2012 年 3 月