
第4章平面和空间向量 线性系统的许多重要特性可以用向量的概念来描 述,因为向量可以描述两个或两个以上的实数组 成的数组特征。二维和三维空间中的向量有鲜明 的几何意义,也有广泛的应用价值,掌握它们的 基本特性就可更好地从几何空间概念来理解线性 代数方程组的某些性质,同时也可帮助人们去抽 象推想高维的向量空间。,本章将介绍向量空间的 基本概念,用它来进一步诠释线性方程组的几何 意义;以便从几何概念过渡到代数推理,进而用 数学软件来解决它们的计算问题。下一章则讨论 二、三向量线性变换中一些较深入的问题
第4章 平面和空间向量 线性系统的许多重要特性可以用向量的概念来描 述,因为向量可以描述两个或两个以上的实数组 成的数组特征。二维和三维空间中的向量有鲜明 的几何意义,也有广泛的应用价值,掌握它们的 基本特性就可更好地从几何空间概念来理解线性 代数方程组的某些性质,同时也可帮助人们去抽 象推想高维的向量空间。本章将介绍向量空间的 基本概念,用它来进一步诠释线性方程组的几何 意义;以便从几何概念过渡到代数推理,进而用 数学软件来解决它们的计算问题。下一章则讨论 二、三向量线性变换中一些较深入的问题

4.1向量的类型 ·物理向量:向量这个术语起源于物理,用以表示既有大小 又有方向的物理量,如力,位移和速度等。那些只需用一 个实数来表示的物理量,如温度、压力和质量等就称为标 量。向量还可以有更广泛的意义,可以把任何由多个参数 描述的变量视为向量。如: ·1)一个班的学生本学期学了五门课,则每人的成绩就可 用五个分数组成的向量来反映; ·5).把人口按年龄分别统计可以得到一个具有100多维的 向量,如再按性别分开,得到的是200多维的向量。 。 不难看出,向量的引入极大地扩展了对象建模的深度和广 度
4.1 向量的类型 • 物理向量:向量这个术语起源于物理,用以表示既有大小 又有方向的物理量,如力,位移和速度等。那些只需用一 个实数来表示的物理量,如温度、压力和质量等就称为标 量。向量还可以有更广泛的意义,可以把任何由多个参数 描述的变量视为向量。如: • 1)一个班的学生本学期学了五门课,则每人的成绩就可 用五个分数组成的向量来反映; • … … • 5).把人口按年龄分别统计可以得到一个具有100多维的 向量,如再按性别分开,得到的是200多维的向量。 • 不难看出,向量的引入极大地扩展了对象建模的深度和广 度
几何向量和位置向量 ● 几何向量:把平面上 y 的向量的箭尾A的坐 标值取为(a1,a2),而 B (b1:62) 把箭头所处的点B的 坐标值取为(b1,b2), -◆Q(b1,a2) PP(b1-a1,b2-a2) 联接A点到B点的箭 A(a1,a2) 头就称为几何向量。 用v=AB示: 0 A称为向量的起点,而B称为向量的终点。这样的几何 向量,要用a1,a2,b1,b2四个实数才能表示。 把向量的箭尾A移到原点,箭头B就移到P点。这时的向 量作用线通过了原点,称为位置向量
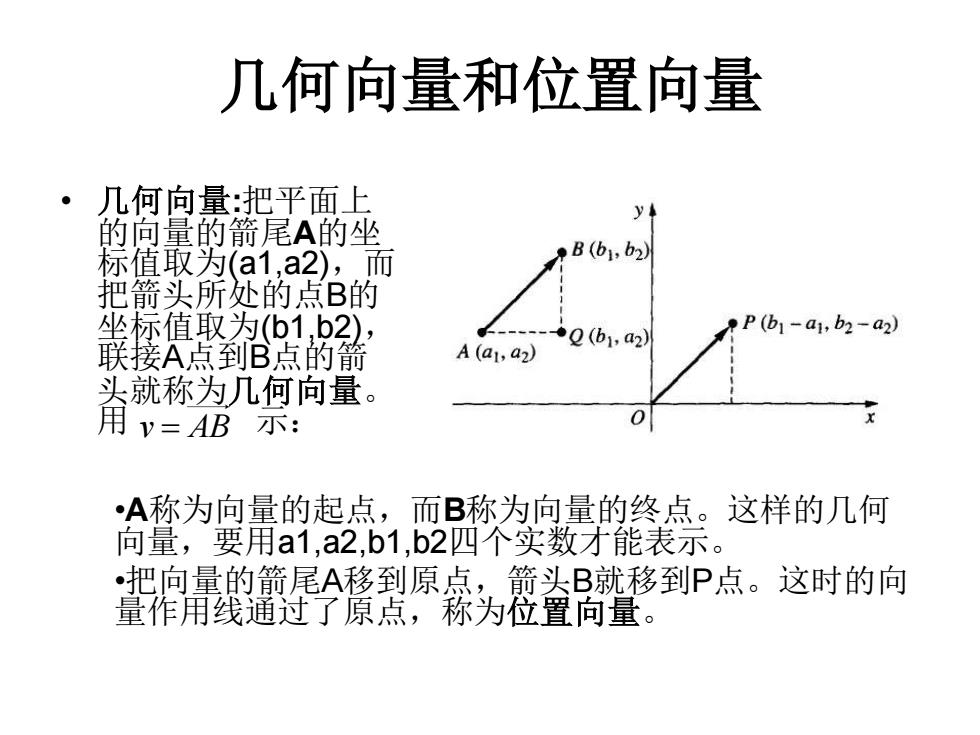
几何向量和位置向量 • 几何向量:把平面上 的向量的箭尾A的坐 标值取为(a1,a2),而 把箭头所处的点B的 坐标值取为(b1,b2), 联接A点到B点的箭 头就称为几何向量。 用 示: •A称为向量的起点,而B称为向量的终点。这样的几何 向量,要用a1,a2,b1,b2四个实数才能表示。 •把向量的箭尾A移到原点,箭头B就移到P点。这时的向 量作用线通过了原点,称为位置向量。 v AB =

代数向量 ·代数向量:把平面中的几何向量V用它在和y两个 方向的分量x和Vy来表示,写成表示式: ·这就是平面中用线性代数表示向量的方法。粗看 起来,它与几何向量的表示法没有太大的差别, 但到了三维以上,几何向量将失去意义,而代数 向量的维数可以无限地扩展,以满足工程和经济 模型分析的需要。从几何到代数,也就是从三维 向高维抽象的线性代数方法论
代数向量 • 代数向量:把平面中的几何向量v用它在x和y两个 方向的分量vx和vy来表示,写成表示式: • • 这就是平面中用线性代数表示向量的方法。粗看 起来,它与几何向量的表示法没有太大的差别, 但到了三维以上,几何向量将失去意义,而代数 向量的维数可以无限地扩展,以满足工程和经济 模型分析的需要。从几何到代数,也就是从三维 向高维抽象的线性代数方法论。 1 1 2 2 x y v b a v b a − = = − v

4.2向量及其线性组合 ·4.2.1平面和空间向量的矩阵表示 平面中的向量v用它在x和y两个方向的分量V1和v2来表示, 行向量写成v1,v2],列向量时为v= 为了节省 V 篇幅,有时按向量转置的规则,把列向量写成[V1,2]T。 ·例4.1设 ]{ 要求画出这两个向量的图形。 解:u和V都是二维空间的列向量。可以用平面坐标系中的 两个点,或从坐标原点引向这两点的箭头来表示
4.2 向量及其线性组合 • 4.2.1 平面和空间向量的矩阵表示 平面中的向量v用它在x和y两个方向的分量v1和v2来表示, 行向量写成[v1,v2],列向量时为 ,为了节省 篇幅,有时按向量转置的规则,把列向量写成[v1,v2]T 。 • 例4.1 设 要求画出这两个向量的图形。 解:u和v都是二维空间的列向量。可以用平面坐标系中的 两个点,或从坐标原点引向这两点的箭头来表示。 1 2 v v = v 1 1 2 2 2 3 , , 4 1 u v u v = = = = − u v
绘制平面向量的程序 也可以用程序pla401来画,得到的 图形见右图。图中也给出了: U-V u+v= 4-y 42-y2 程序pla401的核心语句为: u=[2;4],V=[3;-1] drawvec(u),hold on drawvec(v,'b'),hold on -3-2-1 2345 drawvec(u+v,'g'),hold on drawvec(u-v,'m'),hold off grid on
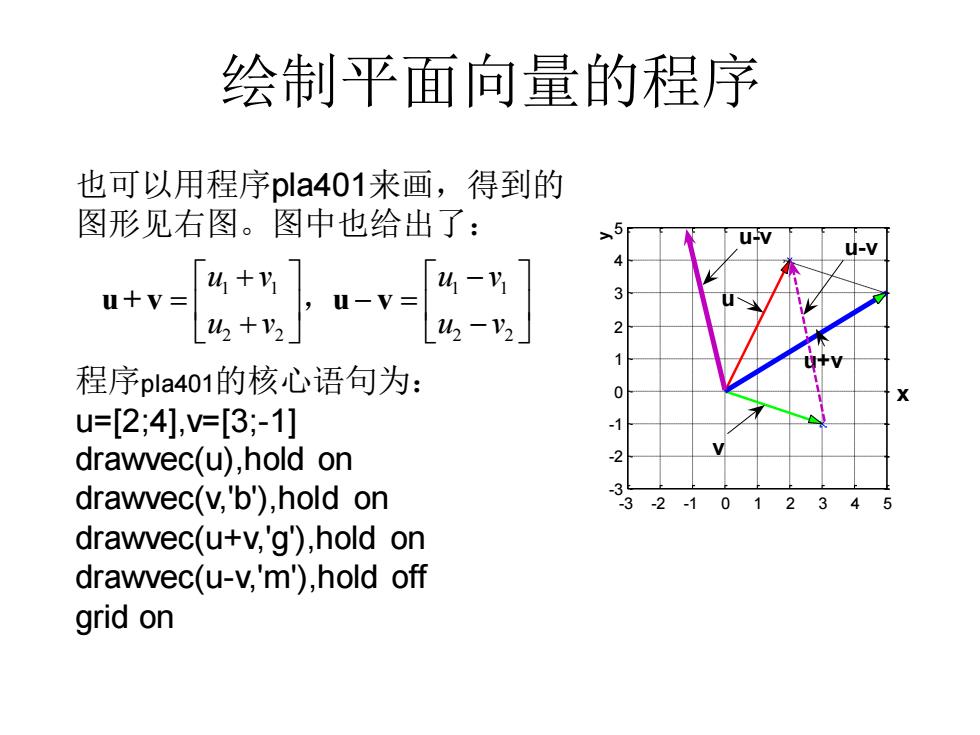
绘制平面向量的程序 -3 -2 -1 0 1 2 3 4 5 -3 -2 -1 0 1 2 3 4 5 x y u-v u+v u v u-v 也可以用程序pla401来画,得到的 图形见右图。图中也给出了: 程序pla401的核心语句为: u=[2;4],v=[3;-1] drawvec(u),hold on drawvec(v,'b'),hold on drawvec(u+v,'g'),hold on drawvec(u-v,'m'),hold off grid on 1 1 1 1 2 2 2 2 u v u v u v u v + − = − = + − u + v u v

向量的加减 ·几何向量的加减按平行四边形法则进行,它在笛卡儿坐标 中的分量则满足简单的代数加减法。对于如图所示的平面 上的二维向量,写成代数形式,为: u+v= 4+y W-Y= 4-y u2+y2 2-y2 向量的线性组合:设c,d为任意数(标量),则表示了向 量u,v的任意线性组合。取例题4.1中的u和V,得到: 。 在图4-2中也画出了c=1和d=-1时的这两个合成向量。不 管c,d取什么值,合成向量b一定是处在x-y平面上;具有 这种性质向量b的全体称为一个二维的向量空间
向量的加减 • 几何向量的加减按平行四边形法则进行,它在笛卡儿坐标 中的分量则满足简单的代数加减法。对于如图所示的平面 上的二维向量,写成代数形式,为: • 向量的线性组合:设c,d为任意数(标量),则表示了向 量u,v的任意线性组合。取例题4.1中的u和v,得到: • 在图4-2中也画出了c=1和d=-1时的这两个合成向量。不 管c,d取什么值,合成向量b一定是处在x-y平面上;具有 这种性质向量b的全体称为一个二维的向量空间。 1 1 1 1 2 2 2 2 u v u v u v u v + − = − = + − u + v u v , 2 3 2 3 4 1 4 c d c d c d c d + = = + = − − b u + v 1 2 b = , b
三维空间的向量加减 ·对于空间向量,用下标1,2,3分别表示笛卡儿坐标xy,z方 向的分量,可类似地推得: 4 4+y [4-v 。若= ,V= 则 u+v= u2+V2 ,u-V= 42-V2 V3 L私+」 4-3 例4.2设列向量u=[1;-2;2],V=[-2;3;-1],求u+V,u-V, 1 2 解:写成列向量: W= 2 ,V= 2 -1 「3 「-1 wl=u+v= -1 w2=u-v- -3 1 1. 3
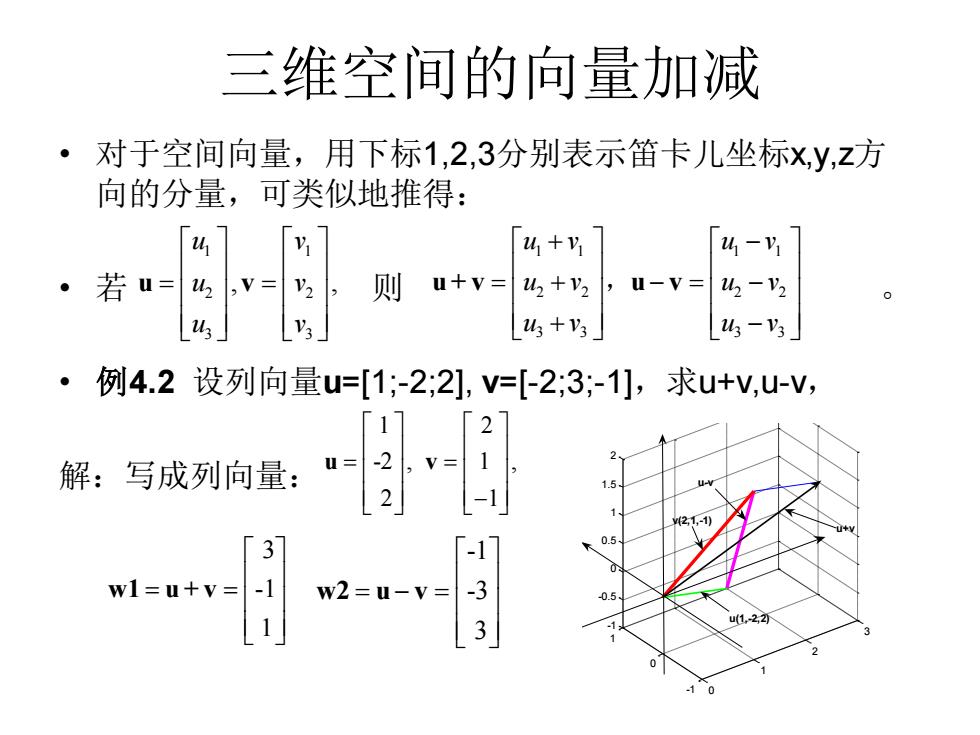
三维空间的向量加减 • 对于空间向量,用下标1,2,3分别表示笛卡儿坐标x,y,z方 向的分量,可类似地推得: • 若 则 。 • 例4.2 设列向量u=[1;-2;2], v=[-2;3;-1],求u+v,u-v, 解:写成列向量: 1 1 2 2 3 3 , , u v u v u v = = u v 1 1 1 1 2 2 2 2 3 3 3 3 u v u v u v u v u v u v + − = + − = − + − u + v u v , 1 2 -2 , 1 , 2 1 = = − u v 3 -1 1 = = w1 u + v -1 -3 3 = − = w2 u v 0 1 2 3 -1 0 1 -1 -0.5 0 0.5 1 1.5 2 u+v u(1,-2,2) v(2,1,-1) u-v

三维空间中的两维向量空间 我们希望读者在学习线性代数时,把三维向量的 矩阵表达式与它们的在三维空间的形状结合起来 ,所以给出了向量uV,w1,w2的立体图。读者可 以自己在草稿纸上练习。 要注意图中u,V两个向量在三维空间组成一个平面 ,它们的合成向量w1,w2必定也在这个平面上, 这在几何上可以想象,但图示就不易看清。,在本 书的程序集中,收藏了它的三维图形,文件名是 fpla403.fig,读者可以在MATLAB命令或☒形窗中 调出这个文件,然后点击其三维旋转按钮,将能 观察到空间向量u,V,w1,w2都处在一个平面上。 也可以说这个平面是,一个二维向量空间,向量 u,V,w1,w2处在同一个向量空间币
三维空间中的两维向量空间 • 我们希望读者在学习线性代数时,把三维向量的 矩阵表达式与它们的在三维空间的形状结合起来 ,所以给出了向量u,v,w1,w2的立体图。读者可 以自己在草稿纸上练习。 • 要注意图中u,v两个向量在三维空间组成一个平面 ,它们的合成向量w1,w2必定也在这个平面上, 这在几何上可以想象,但图示就不易看清。在本 书的程序集中,收藏了它的三维图形,文件名是 fpla403.fig,读者可以在MATLAB命令或图形窗中 调出这个文件,然后点击其三维旋转按钮,将能 观察到空间向量u,v,w1,w2都处在一个平面上。 也可以说这个平面是一个二维向量空间,向量 u,v,w1,w2处在同一个向量空间中

4.2.2向量的几何长度和方向余弦 (0.0,3)5 (0,2) 1(1.2】 /1,2.3) ++喝 5=12+22 14=12+22+32 (0.2,0 (1.0 (1.0.0) (1,2.0) 向量几何长度的符号为,在直角坐标系中,几何长度 为它的各个分量的平方和的开方。图4-4表示二维向量(1,2) 的几何长度为=√+2)=5,三维向量(1,2,3)的几何 长度为√P+22+32)=√4。 ·线性代数中常常把向量中所包含的元素数称为长度,二维 向量的长度为2,三维向量的长度为3。MATLAB中用 length命令求向量的元素数,而用norm(译为“范数”) 命令来求几何长度,读者要注意避免把这两者相混淆
4.2.2 向量的几何长度和方向余弦 • 向量几何长度的符号为 ,在直角坐标系中,几何长度 为它的各个分量的平方和的开方。图4-4表示二维向量(1,2) 的几何长度为 ,三维向量(1,2,3)的几何 长度为 。 • 线性代数中常常把向量中所包含的元素数称为长度,二维 向量的长度为2,三维向量的长度为3。MATLAB中用 length命令求向量的元素数,而用norm(译为“范数”) 命令来求几何长度,读者要注意避免把这两者相混淆。 v 2 2 v = + = (1 2 ) 5 2 2 2 (1 2 3 ) 14 + + =