
线性代数实践(第四讲) 第9章 线性变换及其特征
线性代数实践(第四讲) 第9章 线性变换及其特征

9.1平面上线性变换的几何意义 。 例9.1设x为二维平面上第一象限中的一个单位方块,其 四个顶点的数据可写成 x- 把不同的A矩阵作用于此组数据,可以得到多种多样的结果 yi=Ai*x。用程序ag911进行变换计算,并画出x及yi图形: X=[0,1,1,0;0,0,1,1] subplot(2,3,1),fil(x(1,),0],x(2,),0],'r) A1=[-1,0;0,1],y1=A1*X subplot(2,3,2),fill(y1(1,),0],y1(2,),0],'g)
9.1 平面上线性变换的几何意义 • 例9.1 设x为二维平面上第一象限中的一个单位方块,其 四个顶点的数据可写成 把不同的A矩阵作用于此组数据,可以得到多种多样的结果 yi=Ai*x。用程序ag911进行变换计算,并画出x及yi图形: x=[0,1,1,0;0,0,1,1]; subplot(2,3,1), fill([x(1,:),0],[x(2,:),0],'r') A1=[−1,0;0,1], y1=A1*x subplot(2,3,2), fill([y1(1,:),0],[y1(2,:),0],'g') … 0 1 1 0 0 0 1 1 x =
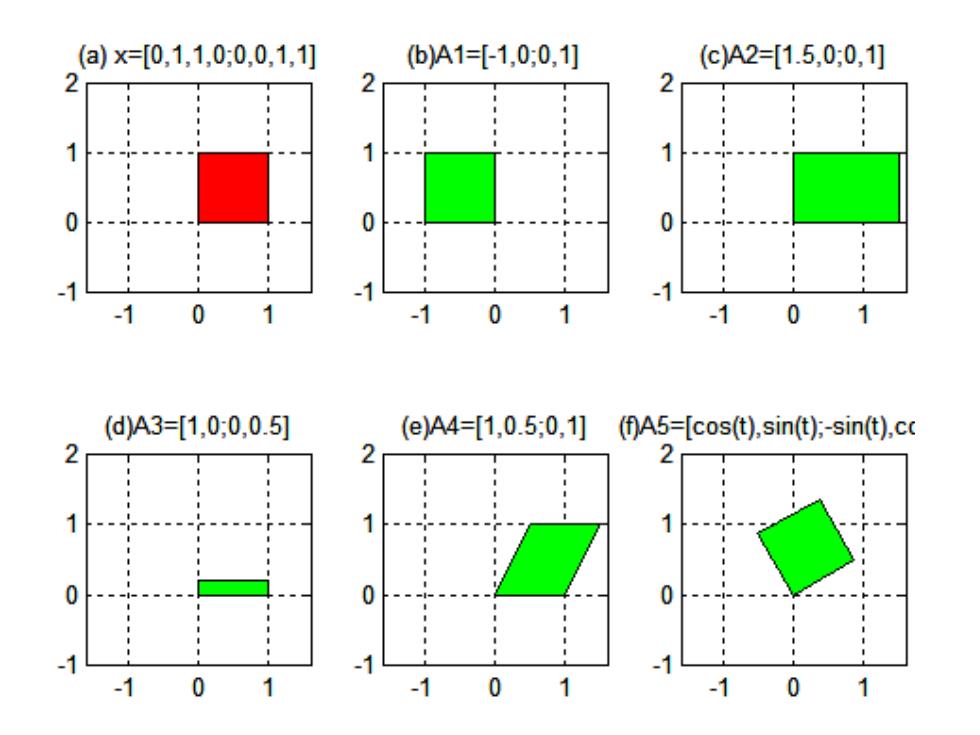
(a)x=[0,1,1,0:0,0,1,1 (b)A1=[-1,0:0,1] (c)A2=[1.5,0;0,1 2 2 2 1 1 0 0 0 0 0 0 (dA3=[1,0:0,0.5 (e)A4=[1,0.5;0,1](0A5=[cost),sint:-sint),cc 2 0 0 0 0
图 9.1 对单元方格进行几种线性变换后生成的图形

几种变换的行列式与特征值 1=d0=-1N=-1小1-[09] m-a-15.2-015Lp2-[9 3=dw4-02,8-0210-[日 D4=det(A4)=1,24=[11 D5=L25=-[086+05i0866-0.5i],p5=[ .7071 0.7071 0-0.7071i0+0.7071i
几种变换的行列式与特征值 1 0 1 det( 1) 1, 1 1 1 , 1 0 1 0 1 2 det( 2) 1.5, 2 1.0 1.5 , 2 1 0 0 1 3 det( 3) 0.2, 3 0.2 1.0 , 3 1 0 1.0 1.0 4 det( 4) 1, 4 1 1 , 4 0. D A p D A p D A p D A p = = − = − = = = = = = = = = − = = = = 0. 0.7071 0.7071 5 1, 5 0.866 + 0.5i 0.866 0.5i , 5 0 0.7071i 0 + 0.7071i D p = = − = −

看出的基本关系 可以看出,矩阵A1使原图对纵轴生成镜像,矩阵 A2使原图在横轴方向膨胀,矩阵A3使原图在纵轴 方向压缩,矩阵A4使原图向右方剪切变形,矩阵 A5使原图沿反时针方向旋转t=pi/6。分别计算出 这五个矩阵的行列式和特征值, 。 对二维空间(平面),行列式的几何意义实际上 是两个向量所构成的平行四边形的面积。一个变 换所造成的图形的面积变化,取决于该变换的行 列式。A1,A4和A5的行列式绝对值都是1,所以 它们不会使变换后图形的面积发生改变。而A2和 A3的行列式分别为1.5和0.2
看出的基本关系 • 可以看出,矩阵A1使原图对纵轴生成镜像,矩阵 A2使原图在横轴方向膨胀,矩阵A3使原图在纵轴 方向压缩,矩阵A4使原图向右方剪切变形,矩阵 A5使原图沿反时针方向旋转t=pi/6。分别计算出 这五个矩阵的行列式和特征值, • 对二维空间(平面),行列式的几何意义实际上 是两个向量所构成的平行四边形的面积。一个变 换所造成的图形的面积变化,取决于该变换的行 列式。A1,A4和A5的行列式绝对值都是1,所以 它们不会使变换后图形的面积发生改变。而A2和 A3的行列式分别为1.5和0.2

9.2二维矩阵特征值的几何意义 二维矩阵的特征值表示该变换在原图形的特征向 量的方向上的放大量。例如矩阵A1在第一特征向 量p(,)= 0方向的特征值为(四=-1, 即横轴 正方向的增益为-1,其结果是把原图中横轴正方 向的部分变换到新图的负方向去了;A1在第二特 0 征向量pl(:,2)= 的方向的特征值为入1(2)=1, 即纵轴正方向的增益为1,因而保持了新图和原 图在纵轴方向尺度不变
9.2 二维矩阵特征值的几何意义 • 二维矩阵的特征值表示该变换在原图形的特征向 量的方向上的放大量。例如矩阵A1在第一特征向 量 方向的特征值为 ,即横轴 正方向的增益为−1,其结果是把原图中横轴正方 向的部分变换到新图的负方向去了;A1在第二特 征向量 的方向的特征值为λ1(2)=1, 即纵轴正方向的增益为1,因而保持了新图和原 图在纵轴方向尺度不变。 1 1(:,1) 0 p = 1(1) 1 = − 0 1(:,2) 1 p =

用eigshowi函数看特征值 o 对于比较复杂的情况,完全凭简单的几何关系去想 像是困难的,应当用eigshow函数,联系x和Ax的 向量图来思考。 ·键入eigshow(A4)。绿色的x表示原坐标系中的单 位向量,可以用鼠标左键点住并拖动它围绕原点 转动。图中同时出现以蓝色表示的Ax向量,它表示 变换后的新向量。当两个向量处在同一条直线上时 (包括同向和反向),表示两者相位相同,只存在 一个(可正可负的)实数乘子入, AX=λX
用eigshow函数看特征值 • 对于比较复杂的情况,完全凭简单的几何关系去想 像是困难的,应当用eigshow函数,联系x和Ax的 向量图来思考。 • 键入eigshow(A4) 。绿色的x表示原坐标系中的单 位向量,可以用鼠标左键点住x并拖动它围绕原点 转动。图中同时出现以蓝色表示的Ax向量,它表示 变换后的新向量。当两个向量处在同一条直线上时 (包括同向和反向),表示两者相位相同,只存在 一个(可正可负的)实数乘子λ, • Ax=λx
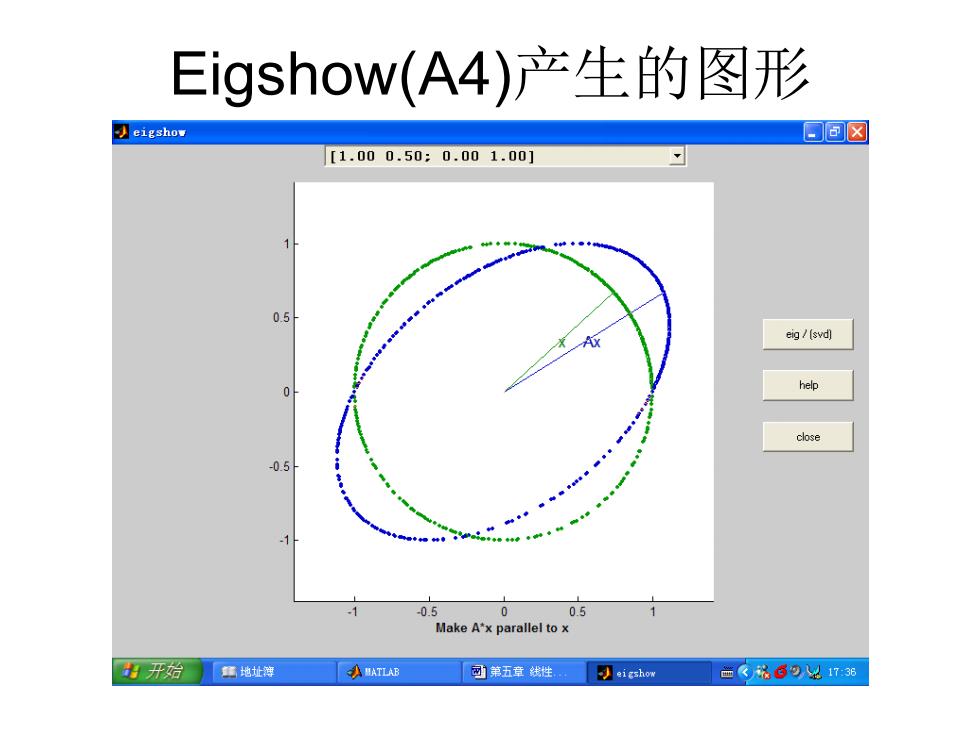
Eigshow(A4)产生的图形 eigshow 口@☒ 【1.000.50:0.001.00] eig/(svd] help close -05 0.5 Make A'x parallel to x 开始马地址裤 人ATLAB 厂可第五章线牲)eihm 画《86可1736
Eigshow(A4)产生的图形
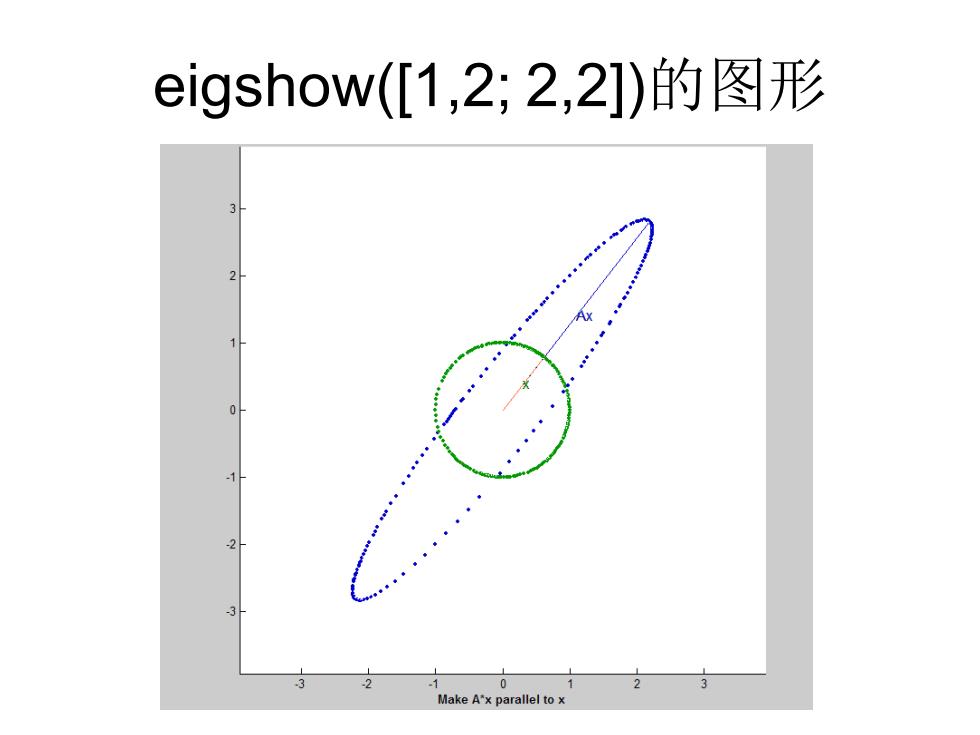
eigshow([1,2;2,2])的图形 0 Make A'x parallel to x
eigshow([1,2; 2,2])的图形

A是对称实矩阵的情况 ·特别要注意A是对称实矩阵的情况,所谓对 称矩阵是满足AT=A的矩阵。,对2×2矩阵, 只要求A(1,2)=A(2,1)。例如令,A=[1,2;2,2] 再键入eigshow(A),这时的特点是:Ax=x 出现在Ax椭圆轨迹的主轴上,所以两个特 征值分别对应于单位圆映射的椭圆轨迹的 长轴和短轴。此时A的特征值为-0.5616和 3.5616,可以和图形对照起来看
A是对称实矩阵的情况 • 特别要注意A是对称实矩阵的情况,所谓对 称矩阵是满足AT=A的矩阵。,对22矩阵, 只要求A(1,2)=A(2,1)。例如令,A=[1,2;2,2] 再键入eigshow(A),这时的特点是:Ax=λx 出现在Ax椭圆轨迹的主轴上,所以两个特 征值分别对应于单位圆映射的椭圆轨迹的 长轴和短轴。此时A的特征值为 -0.5616和 3.5616,可以和图形对照起来看