《实用大众线性代数》课程参考文献（MATLAB版）线性代数在科技及工程中的应用实例

第7章在科技及工程中的应用实例 7.1由拉压杆组成的桁架结构… 72格型梯形滤波器系统函数的推号 7.3计算频谱用的DFT矩阵 74显示器色彩制式转换问期 7.5人员流动问题 7.6一氧化碳分子结构的振动频率 5 一自由度机城振动 7.8FIR数字滤波器最优化设计2 7.9弹性梁的柔度矩阵 0 7.10用二次样条函数插值5个点 7.11飞行器三维空间运动的矩阵描述 12 7.12金融公司支付基金的流动 14 7.13 质谱图实验结果分析 .15 7.14用特征方程解Fibonacci数列问颗 16 7.15 简单线性规划问题 18

第 7 章 在科技及工程中的应用实例.........................................................................1 7.1 由拉压杆组成的桁架结构........................................................................................................................1 7.2 格型梯形滤波器系统函数的推导 ..........................................................................................................1 7.3 计算频谱用的 DFT 矩阵...........................................................................................................................2 7.4 显示器色彩制式转换问题........................................................................................................................4 7.5 人员流动问题..............................................................................................................................................5 7.6 二氧化碳分子结构的振动频率...............................................................................................................5 7.7 二自由度机械振动.....................................................................................................................................6 7.8 FIR 数字滤波器最优化设计[12] ...............................................................................................................8 7.9 弹性梁的柔度矩阵.....................................................................................................................................9 7.10 用二次样条函数插值 5 个点...............................................................................................................11 7.11 飞行器三维空间运动的矩阵描述 ......................................................................................................12 7.12 金融公司支付基金的流动....................................................................................................................14 7.13 质谱图实验结果分析 ..........................................................................................................................15 7.14 用特征方程解 Fibonacci 数列问题 ....................................................................................................16 7.15 简单线性规划问题.................................................................................................................................18

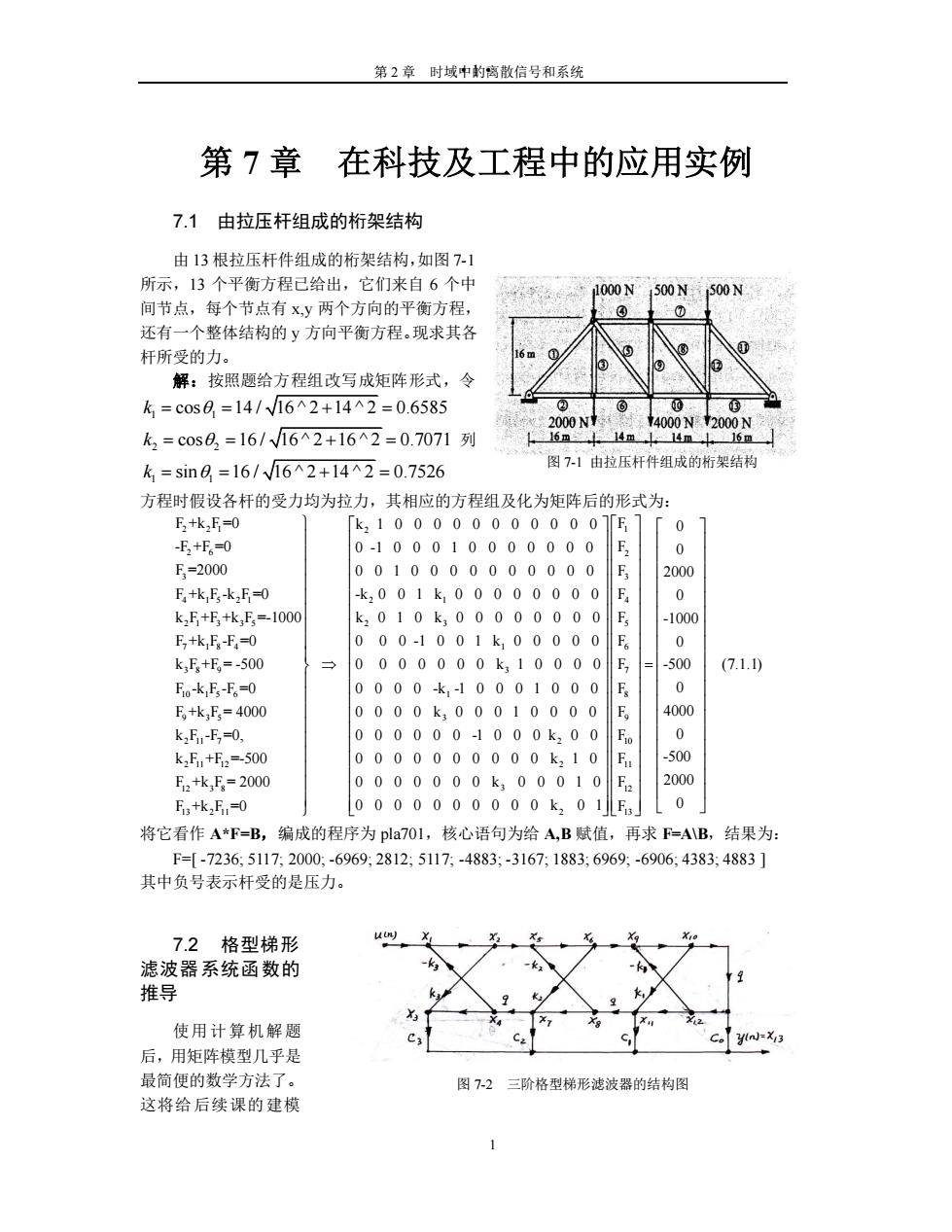
第2章时域中的离散信号和系统 第7章在科技及工程中的应用实例 7.1由拉压杆组成的桁架结构 由13根拉压杆件组成的桁架结构，如图7-】 所示，13个平衡方程已给出，它们来自6个中 间节点，每个节点有Xy两个方向的平衡方程， 还有一个整体结构的y方向平衡方程。现求其各 杆所受的力。 解：按照题给方程组改写成矩阵形式，令 k=c0s8=14/V16^2+14^2=0.6585 k3=c0s8,=16/W16^2+16^2=0.7071列 】14m0 4000N2000 k=sin8=16/√162+14^2=0.7526 图71由拉压杆件组成的析架结料 方程时假设各杆的受力均为拉力，其相应的方程组及化为矩阵后的形式为： F,tk,F■0 「k,1000000000007「E 0 E+F=0 0.100010000000 0 E=2000 0010000000000 000 F+k E-k2F-0 -K.0 0 k,E+5+k,E,=1000 k.010k.00 00 F -1000 E,k,5-E,=0 000-100 000 0 k,+E,=-500 00 50 (7.1.0 E。kEF=0 0000 0 0 E,+k,E=4000 40 k5-f,0, 0 k,F,+E2=-500 00k.10 -50 E2+k,E=2000 00010 2000 F2+k2F1=0 0000000000k201E 0 将它看作A*F=B,编成的程序为pla7O1,核心语句为给A,B赋值，再求F=AB,结果为 F=-7236,5117,2000,-6969,2812;5117;-4883;-3167;1883,6969:-6906:4383,4883] 其中负号表示杆受的是压力。 7.2格型梯形 滤波器系统函数的 推导 使用计算机解题 后，用矩阵模型几乎是 最简便的数学方法了。 图7-2三阶格型梯形滤波器的结构图 这将给后续课的建模

第 2 章 时域中的离散信号和系统 ·1· 1 第 7 章 在科技及工程中的应用实例 7.1 由拉压杆组成的桁架结构 由 13 根拉压杆件组成的桁架结构，如图 7-1 所示，13 个平衡方程已给出，它们来自 6 个中 间节点，每个节点有 x,y 两个方向的平衡方程， 还有一个整体结构的 y 方向平衡方程。现求其各 杆所受的力。 解：按照题给方程组改写成矩阵形式，令 1 1 2 2 1 1 cos 14 / 16 ^ 2 14 ^ 2 0.6585 cos 16 / 16 ^ 2 16 ^ 2 0.7071 sin 16 / 16 ^ 2 14 ^ 2 0.7526 k k k    = = + = = = + = = = + = 列 方程时假设各杆的受力均为拉力，其相应的方程组及化为矩阵后的形式为： 2 2 1 2 2 6 3 4 1 5 2 1 2 1 3 3 5 7 1 8 4 3 8 9 10 1 5 6 9 3 5 2 11 7 2 11 12 12 3 8 13 2 11 F +k F =0 k 1 0 0 0 0 0 0 0 0 0 0 0 -F +F =0 0 - F =2000 F +k F -k F =0 k F +F +k F =-1000 F +k F -F =0 k F +F = -500 F -k F -F =0 F +k F = 4000 k F -F =0, k F +F =-500 F +k F = 2000 F +k F =0                       2 1 2 3 1 3 1 3 2 2 3 2 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 -k 0 0 1 k 0 0 0 0 0 0 0 0 k 0 1 0 k 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 1 k 0 0 0 0 0 0 0 0 0 0 0 0 k 1 0 0 0 0 0 0 0 0 -k -1 0 0 0 1 0 0 0 0 0 0 0 k 0 0 0 1 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 k 0 0 0000000000k 10 0 0 0 0 0 0 0 k 0 0 0 1 0 0000000000k 01                      1 2 3 4 5 6 7 8 9 10 11 12 13 F 0 F 0 F 2000 F 0 F -1000 F 0 F -500 (7.1.1) F 0 F 4000 F 0 F -500 F 2000 F 0                                         =                                           将它看作 A*F=B，编成的程序为 pla701，核心语句为给 A,B 赋值，再求 F=A\B，结果为： F=[ -7236; 5117; 2000; -6969; 2812; 5117; -4883; -3167; 1883; 6969; -6906; 4383; 4883 ] 其中负号表示杆受的是压力。 7.2 格型梯形 滤波器系统函数的 推导 使用计算机解题 后，用矩阵模型几乎是 最简便的数学方法了。 这将给后续课的建模 图 7-1 由拉压杆件组成的桁架结构 图 7-2 三阶格型梯形滤波器的结构图

第2章时域中韵离散信号和系统 和计算带来革命性的好处。例如要求出图7-2所示的滤波器的系统函数： 先列出方程，令q7,得到 =6+,8=g1:=6-KX2,X0=9,1=k0叶X2云，X2=gX0 1=1=C12+C1+C)+C3 这是一组含有13个变量的3个联立方程，用过去的手工方法一个一个消元，理论上是可 行的，但它运算极其繁琐，可以预期，95%以上的师生恐怕一个小时也解不出来，而且做对的 概率极低。 用矩阵的思路和方法来解就完全不同，它不是通过消元来减少变量，而是想办法补上所有 的零元素，把方程扩充为完整的矩阵形式： X =u-kx 0.0.0.-k.0.0.0.0.0.0.0.0.0x 「1 00 0, 00 x=kx,+x 0 0 0. 0. 0 0 0. 0 x=kx+x X 玉= X=X6 u=Xo 000 x,=kX。+x 0.0. 0 1.0 x2=90 2 0.0 0 0 0 0 0.0.0 0 Xg三… x13 0,0,C,0,0,0,C,0,0,0,C.C,0L 台X=OX+PU.→X/U=inwI-O)P 看似把模型搞复杂了，其实计算却非常容易。程序pla703先对P,Q矩阵赋值，键入 W=invI-Q)*P,马上就得出了系统函数。 编程时要注意，本例虽然是数值计算，但计算的内容中带有z变换算子q',所以P,Q 矩阵仍然必须用符号属性，对P,Q赋值时第一个元素必须取含q的算式。熟练后不必列出Q 和P的矩阵形式，可以按其下标规律直接进行元素赋值。 用以下参数：k=1,k1=14,k=12.k=1/3.C0=02,C1=0.8.C=1.5C3=1,编成了程序 pla703。运行此程序就得到： w13)=13)_24g+49g2+42.9g+30.824:+49:2+429e+30.8 8q+15g2+13g+24 8+1522+13z+24 用矩阵模型解信号流图的最大优点是一步到位，依靠计算机，既快速，又极易查错 7.3计算频谱用的DFT矩阵 有限长序列x(m)(0≤n≤1)有W个样本值。它的傅里叶变换X(k)在频率区间(0≤⊙ <2π)的W个等间隔分布的点o=2kN(0≤k≤N-1)上也有N个样本值。这两组有限长的 序列之间可以用简单的关系联系起来： 2

第 2 章 时域中的离散信号和系统 ·2· 2 和计算带来革命性的好处。例如要求出图 7-2 所示的滤波器的系统函数： 先列出方程，令 q=z-1，得到 x1= u− k3x4; x2=x1; x3=k3x2+x4; x4=qx7; x5= x2− k2x8; x6=x5; x7=k2x6+x8; x8=qx11; x9= x6− k1x12; x10=x9; x11=k1x10+x12; x12=qx10; x13=y= C0x12+ C1x11+ C2x7+ C3x3 这是一组含有 13 个变量的 13 个联立方程，用过去的手工方法一个一个消元，理论上是可 行的，但它运算极其繁琐，可以预期，95%以上的师生恐怕一个小时也解不出来，而且做对的 概率极低。 用矩阵的思路和方法来解就完全不同，它不是通过消元来减少变量，而是想办法补上所有 的零元素，把方程扩充为完整的矩阵形式： 1 3 4 2 1 3 3 2 4 4 7 5 2 2 8 6 5 7 2 1 2 3 4 6 5 6 7 8 9 8 8 11 9 6 1 12 10 9 11 1 10 12 12 10 13 10 11 12 13 - - - x u k x x x x k x x x qx x x k x x x x k x x x qx x x k x x x x k x x x qx x x x x x x x x x x x x x x = = = + = = = =                                                       + = =   = = + = = 3 3 0, 0, 0, - , 0, 0, 0, 0, 0, 0, 0, 0, 0 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 0, , 0, 1, 0, 0, 0, k k =         2 0, 0, 0, 0, 0, 0 0, 0, 0, 0, 0, 0, q, 0, 0, 0, 0, 0, 0 0, 1, 0, 0, 0, 0, 0, - , 0, 0, 0, 0, 0 0, 0, 0, k 2 0, 1, 0, 0, 0, 0, 0, 0, 0, 0 0, 0, 0, 0, 0, , 0, 1, 0, 0, 0, 0, 0 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, q, 0, k 1 0 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, - , 0 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0 0, 0, 0, 0, 0, 0, 0, 0, k 1 3 2 1 0 0, , 0, 1, 0 0, 0, 0, 0, 0, 0, 0, 0, 0, q, 0, 0, 0 0, 0, C , 0, 0, 0, C , 0, 0, 0, C , C , 0 k                     1 2 3 4 5 6 7 8 9 10 11 12 13 1 0 0 0 0 0 0 0 0 0 0 0 0 x x x x x x x u x x x x x x                                         +                                             X = QX + PU X U = inv(I - Q)* P , / 看似把模型搞复杂了，其实计算却非常容易。程序 pla703 先对 P，Q 矩阵赋值，键入 W = inv(I - Q)* P ，马上就得出了系统函数。 编程时要注意，本例虽然是数值计算，但计算的内容中带有 z 变换算子 q=z-1，所以 P，Q 矩阵仍然必须用符号属性，对 P，Q 赋值时第一个元素必须取含 q 的算式。熟练后不必列出 Q 和 P 的矩阵形式，可以按其下标规律直接进行元素赋值。 用以下参数：k0=1, k1=1/4, k2=1/2, k3=1/3, C0=-0.2, C1=0.8, C2=1.5, C3=1，编成了程序 pla703。运行此程序就得到： 3 2 3 2 1 3 2 3 2 1 (13) 24 49 42.9 30.8 24 49 42.9 30.8 (13) 8 15 13 24 8 15 13 24 x q q q z z z W u q q q z z z − − − − − − = + + + + + + = = + + + + + + 用矩阵模型解信号流图的最大优点是一步到位，依靠计算机，既快速，又极易查错。 7.3 计算频谱用的 DFT 矩阵 有限长序列 x(n)(0≤n≤N-1)有 N 个样本值。它的傅里叶变换 X k( ) 在频率区间（0≤ω ＜2π）的 N 个等间隔分布的点ωk=2πk/N(0≤k≤N-1)上也有 N 个样本值。这两组有限长的 序列之间可以用简单的关系联系起来：

第2章时域中的离散信号和系统 0≤k≤N-1 其中W=xp(2πj/N)是一个相角2π/N为的单位向量，也称为旋转因子。()就 称为x()的离散傅里叶变换(DFT),也就是x)的频谱。用矩阵来表示，可写成： 1 1 1 X(0 型 形 「x0) O) =1 部 形w -W.x X(N-1] W(N-1IN-1 x(N-1) W 所以信号频谱的计算，可以简单地用一个矩阵乘法来完成。信号是NX1维数组，矩阵 W称为DFT矩阵，它是NXN维的复数阵。把矩阵乘法看作一个变换，我们就可以把频谱计 算看作信号从时域到频域的线性变换。 这个矩阵运算可用下列几条MATLAB语句来实现，程序名为pla7O4。 m=input xn=长度为N的数组) .N=1 ongth(m)%输入据 n=[0:1:N-1]:k=[0:1:N-1: %没定n和k的行向量 J*21/0 Nk=N.·nk %求出W 含k值的N乘N维的整数矩阵 从=Xn*Nk 多求出离散傅里叶级数系数 两条语句无须解释。第三条语句把n转为列向量'，再与行向量k做矩阵乘，它产 生的是 整数矩阵： 0 2 [0.12.N-11■ 0 2x(N-D) W-1 0N-1.N-1D×N-1D 这个整数方阵恰好是算式X=Wx中W矩阵的指数部分第四条语句就产生了矩阵， 而最后一条语句就完成了DFS的全部运算。由于实际上离散傅里叶级数并不太用到。它已 被下节将介绍的离散傅里叶变换取代，而且两者的计算程序是完全相同的。所以如果写成 MATLAB子程序，它可以命名为DFT。 在这5行DFT子程序前面，加上输入语句： n=input ('xn=')N=length(xn); 在子程序后面，加上绘图语句： 0.5 就得到本题的程序p1a604。 100 200 100 运行D1a604, 并按提示输入x,即可在子图1 50 上得到x序列的波形 ,并在子图2 上得到此信号的幅 频特性。例如输入序列为 100 200 Xn=[ones(1,64),zeros(1,192)],则得到的时域 图7-3序列x()及其频诺 波形及其频谱图如图7-3。 计算每一个DFT分量()，需要做W次复数乘法和：1次复数加法。而要完成整个 DFT,求出K,则需要做XW次复数乘法和（心1）次复数加法。另外，它占的数据存储量 为仪M。在频谱计算中，N的典型值是1024。所以参与运算的数据达百万，需要的存储量

第 2 章 时域中的离散信号和系统 ·3· 3 1 ( ) ( ) 0 1 N kn N n k x n W k N − X =   −  其中 W j N N = exp 2 / (  ) 是一个相角 2 /  N 为的单位向量，也称为旋转因子。X(k)就 称为 x(n)的离散傅里叶变换(DFT)，也就是 x(n)的频谱。用矩阵来表示,可写成: 所以信号频谱的计算，可以简单地用一个矩阵乘法来完成。信号是 N×1 维数组，矩阵 W 称为 DFT 矩阵，它是 N×N 维的复数阵。把矩阵乘法看作一个变换，我们就可以把频谱计 算看作信号从时域到频域的线性变换。 这个矩阵运算可用下列几条 MATLAB 语句来实现，程序名为 pla704。 xn=input('xn=(长度为 N的数组) '), N=length(xn); % 输入数据 n = [0:1:N-1]; k = [0:1:N-1]; % 设定 n 和 k 的行向量 WN = exp(-j*2*pi/N); % 设定 Wn 因子 nk = n'*k; % 产生一个含 nk 值的N 乘N 维的整数矩阵 WNnk = WN .^ nk; % 求出 W 矩阵 Xk = xn * WNnk % 求出离散傅里叶级数系数 plot(k,Xk) % 画出幅频特性 前两条语句无须解释。第三条语句把 n 转为列向量 n’，再与行向量 k 做矩阵乘，它产 生的是一个整数矩阵： 这个整数方阵恰好是算式 中 W 矩阵的指数部分。第四条语句就产生了W 矩阵， 而最后一条语句就完成了 DFS 的全部运算。由于实际上离散傅里叶级数并不太用到。它已 被下节将介绍的离散傅里叶变换取代，而且两者的计算程序是完全相同的。所以如果写成 MATLAB 子程序，它可以命名为 DFT。 在这 5 行 DFT 子程序前面，加上输入语句： xn=input('xn= '); N=length(xn); 在子程序后面，加上绘图语句： subplot(2,1,1),stem(xn,'.'); subplot(2,1,2),stem(abs(Xk),'.') 就得到本题的程序 pla604。 运行 pla604，并按提示输入 xn，即可在子图 1 上得到 xn 序列的波形，并在子图 2 上得到此信号的幅 频特性。例如输入序列为 xn=[ones(1,64),zeros(1,192)]，则得到的时域 波形及其频谱图如图 7-3。 计算每一个 DFT 分量 X(i)，需要做 N 次复数乘法和 N-1 次复数加法。而要完成整个 DFT，求出 X，则需要做 N×N 次复数乘法和 N(N-1)次复数加法。另外，它占的数据存储量 为 N×N。在频谱计算中，N 的典型值是 1024。所以参与运算的数据达百万，需要的存储量 0 100 200 300 0 0.5 1 0 100 200 300 0 50 100 图 7-3 序列 x(n)及其频谱

第2章时域中的离散信号和系统 超过16M,乘法运算的次数超过数百万。因此，在低档的微机上 当N较大时，MATLAB 会拒绝执行这个程序，并警告内存不足。实际上，MATLAB内置的是加快计算并节省内存快 速傅里叶变换(FFT程序。 从这里也可以看出，矩阵给我们提供了一个组织海量数据进行运算的最好方法，对上 百万数据进行赋值、运算和绘图，只用了几行程序。线性代数的重要性之所以在近20年来 可与微积分相妣美，这是一个重要原因。如果学线性代数而不涉及工程计算实践，那就无 法真正体会线性代数的精髓所在。 7.4显示器色彩制式转换问题 彩色显示器使用红(R)、绿(G)和蓝(B)光的叠成效应生成颜色。显示器屏幕的内表面由微粒 象素组成，每个微粒包括三个荧光点：红、绿、蓝。 电子枪位于屏幕的后方，向屏幕上每个点 发射电子束。计算机从图形应用程序或扫描仪发出数字信号到电子枪，这些信号控制电子枪设 置的电压强度.不同RGB的强度组合将产生不同的颜色.电子枪由偏转电磁场帮助瞄准以确 保快速精确地屏幕刷新 每个微粒包括三个荧 光点： 、蓝 8 电子枪吕 显示器屏幕的内表 数字信号 面由微粒象素组成 图形应用程序或扫描仪 图74彩色显示器的工作原理 颜色模型规定一些属性或原色，将颜色分解成不同属性的数字化组合.这就是色彩制式的 转换问题。 观察者在屏幕上实际看到的色彩要受色彩制式和屏幕上荧光点数量的影响。，因此每家计 算机屏幕制造商都必须在(R,G,B)数据和国际通行的C亚色彩标准之间进行转换C正标准使用 三原色，分别称为X,y和Z。针对短余辉荧光点的一类典型转换是 (0.610.290.150)R)X) 0.350.59 0.063 G →Aa=B 0.040.120.787JBz 计算机程序把用CE数据(X)表示的色彩信息流发送到屏幕，求屏幕上的电子枪将这些数据 转换成(R,G,B)数据的方程。现在要根据CE数据(XYZ)计算对应的(R,G,B)数据，就是等式 Aa=B中A和B已知，求a。如果A是可逆矩阵，则由Aa=B可得a=AB. 解：在Matlab命令窗口输入以下命令 A=[0.61,0.29,0.15:0.35,0.59,0.063:0.04,0.12,0.787]:% B=inv(A), 程序执行的结果为： B= 2.2586-1.0395-0.3473 -1.3495 2.3441 0.0696 0.0910 -0.3040 1.277 可见将C正数 整米花6的民用电视信号的发送并不直接采用 方程为a=Bp 4

第 2 章 时域中的离散信号和系统 ·4· 4 超过 16M， 乘法运算的次数超过数百万。因此，在低档的微机上，当 N 较大时，MATLAB 会拒绝执行这个程序，并警告内存不足。实际上，MATLAB 内置的是加快计算并节省内存快 速傅里叶变换(FFT)程序。 从这里也可以看出，矩阵给我们提供了一个组织海量数据进行运算的最好方法，对上 百万数据进行赋值、运算和绘图，只用了几行程序。线性代数的重要性之所以在近 20 年来 可与微积分相妣美，这是一个重要原因。如果学线性代数而不涉及工程计算实践，那就无 法真正体会线性代数的精髓所在。 7.4 显示器色彩制式转换问题 彩色显示器使用红(R)、绿(G)和蓝(B)光的叠成效应生成颜色。 显示器屏幕的内表面由微粒 象素组成, 每个微粒包括三个荧光点: 红、绿、蓝。 电子枪位于屏幕的后方, 向屏幕上每个点 发射电子束。计算机从图形应用程序或扫描仪发出数字信号到电子枪, 这些信号控制电子枪设 置的电压强度. 不同 RGB 的强度组合将产生不同的颜色. 电子枪由偏转电磁场帮助瞄准以确 保快速精确地屏幕刷新。 图 7-4 彩色显示器的工作原理 颜色模型规定一些属性或原色, 将颜色分解成不同属性的数字化组合. 这就是色彩制式的 转换问题。 观察者在屏幕上实际看到的色彩要受色彩制式和屏幕上荧光点数量的影响。. 因此每家计 算机屏幕制造商都必须在(R, G, B)数据和国际通行的 CIE 色彩标准之间进行转换, CIE 标准使用 三原色, 分别称为 X, Y 和 Z。 针对短余辉荧光点的一类典型转换是 0.61 0.29 0.150 0.35 0.59 0.063 0.04 0.12 0.787           R G B           = X Y Z            Aα = β . 计算机程序把用 CIE 数据(X, Y, Z)表示的色彩信息流发送到屏幕，求屏幕上的电子枪将这些数据 转换成(R, G, B)数据的方程。现在要根据 CIE 数据(X, Y, Z)计算对应的(R, G, B)数据, 就是等式 A =  中 A 和 已知, 求。如果 A 是可逆矩阵, 则由 A = 可得 = A −1. 解：在 Matlab 命令窗口输入以下命令 A = [0.61,0.29,0.15;0.35,0.59,0.063;0.04,0.12,0.787]; % B = inv(A), 程序执行的结果为： B = 2.2586 -1.0395 -0.3473 -1.3495 2.3441 0.0696 0.0910 -0.3046 1.2777 可见将 CIE 数据(X, Y, Z)转换成(R, G, B)数据的方程为 =B 在彩色电视技术中，还有许多地方会用到线性变换.比如民用电视信号的发送并不直接采用

第2章时域中的离散信号和系统 (R,G,B)数据，而是使用向量(Y,L,Q)来描述每种颜色其中Y称为亮度信号，I和Q为色差信号 这样的制式可以达到彩色和黑白的兼容如果屏幕是黑白的，则只用到了Y,这比CE数据能提 供更好的单色图象。YIO与“标准”RGB色彩之间的对应如下 [Y1「0.2990.5870.1141「R 1=0.596-0.275-0.321G Q0.212-0.5280.311B 它的逆变换矩连留给读者自行计算 7.5人员流动问题 某试验性生产线每年一月份进行熟练工与非熟练工的人数统计，然后将1/6熟练工支援其 他生产部门，其缺额由招收新的非熟练工补齐。新、老非熟练工经过培训及实践至年终考核有 2/5成为熟练工，假设第一年 月份统计的熟练工和非熟练工各占一半，求以后每年一月份 计的熟练工和非熟练工所占百分比。 设车一月台计的工和丰练工所占百分比分罗为和记成向乙，一 因为第一年统计的然练工和丰熟练工各占一半，所以乙，=：-2 (厂1/2 。为了求以后每年的熟 练工和非熟练工所占百分比，先求工，与乙.的关系式。根据已知条件可得 名++w品号n 1=(1- 9 2 =-号后+w0+3 z-(8M8389}.-a Z1=AZ.=Z.-1==Z1 将A对角化成为A=PAP可得到简明易算的结果：乙1=(PAP）八乙，-=PAPZ,。 键入命令P,D】=eig(A),得P 「0.9701-0.7071] 101 0.24250.7071 D=A-005于是便有： x_「0.9701-0.707i[r01T0.9701-0.7071T0.5)_[0.8-03/2) y10.24250.7071J00.5"L0.24250.7071」（0.50.2+0.31(2) 当n不断增加时，xn1,y1分别趋向于0.8和0.2。 7.6二氧化碳分子结构的振动频率 二氧化碳分子可看成中间一个碳原子，左右分别以弹簧（化学健）联接两个氧原子，构成 一个三质量振动系统（见图7-5）。其方程为： 5

第 2 章 时域中的离散信号和系统 ·5· 5 (R, G, B)数据，而是使用向量(Y, I, Q)来描述每种颜色.其中 Y 称为亮度信号，I 和 Q 为色差信号， 这样的制式可以达到彩色和黑白的兼容.如果屏幕是黑白的, 则只用到了 Y，这比 CIE 数据能提 供更好的单色图象。YIQ 与“标准”RGB 色彩之间的对应如下 Y I Q           = 0.299 0.587 0.114 0.596 0.275 0.321 0.212 0.528 0.311     − −       − R G B           它的逆变换矩阵留给读者自行计算。 7.5 人员流动问题 某试验性生产线每年一月份进行熟练工与非熟练工的人数统计, 然后将 1/ 6 熟练工支援其 他生产部门, 其缺额由招收新的非熟练工补齐。新、老非熟练工经过培训及实践至年终考核有 2 / 5 成为熟练工，假设第一年一月份统计的熟练工和非熟练工各占一半，求以后每年一月份统 计的熟练工和非熟练工所占百分比。 设第 n 年一月份统计的熟练工和非熟练工所占百分比分别为 xn 和 yn, 记成向量 n n x y   =     Zn . 因为第一年统计的熟练工和非熟练工各占一半, 所以 1 1 x y   =     Z1 = 1/ 2 1/ 2       。为了求以后每年的熟 练工和非熟练工所占百分比, 先求 Zn+1 与 Zn 的关系式。根据已知条件可得: xn+1 = (1− 1 6 )xn + 2 5 ( 1 6 xn + yn) = 9 10 xn + 2 5 yn, yn+1 = (1− 2 5 )( 1 6 xn + yn) = 1 10 xn + 3 5 yn, 即 9 /10 2 / 5 1/10 3 / 5   =     Zn+1 Z = AZ n n Zn+1 = A Zn = A 2 Zn 1− = … = A n Z1 . 将 A 对角化成为 = -1 A PΛP 可得到简明易算的结果： Zn+1 = ( ) 1 1 = n -1 n -1 PΛP P Z Z Λ P 。 键入命令[P,D] = eig(A)，得 0.9701 0.7071 0.2425 0.70 1 0 , 71 0 0.5     = = =      −    P D Λ ，于是便有： 1 1 1 0.9701 0.7071 0.9701 0.7071 0.8 0.3/ (2 ) 0.2425 0.7071 0.2425 1 0 0.5 0 0.5 0.7071 0.5 0.2 0.3/ (2 ) n n n n n n x y − + +               = =                     −  − +  − , 当 n 不断增加时， n 1 x + ， n 1 y + 分别趋向于 0.8 和 0.2。 7.6 二氧化碳分子结构的振动频率 二氧化碳分子可看成中间一个碳原子，左右分别以弹簧（化学键）联接两个氧原子，构成 一个三质量振动系统（见图 7-5）。其方程为：

第2章时域中的离散信号和系统 o@—⑥ d-x. m=-2,++c dx=o,k, 园M园Mw四 设三个原子沿轴向的振动具有同样的频率©， 图7-5C02分子振动结构 ,=A,e,则代入上式后得到： -024= -o24=-2k m +4+4 4点4 4 写成矩阵形式为： m。 %4=0 -4- [k-d- m。 0 4.4 40 k k m。 (2k- k 4=0 m me 4 k k k 0 02 m m, 振动的频率的平方就决定于这个系数矩阵的特征值，因为有三个特征值，要取其中的最大 值。由此写出计算程序pla706,核心语句为： k=14.2e2.m0=16◆1.6605e-27.mc=12◆1.6605e-27. A-[k/mo.-k/mo.0:-k/mc.2*k/mc.-k/mc:0.-k/mo.k/mo]. x.y=eig(A),omega=sqrt(y) lamda=2+pi*3*108./max(max(omega)) 其运行结果如下。答案为： omega 1.0e+014 及lamda= 4.257951e-006m≈4.3μm 77二自由度机械振动 97,9 图79表示了一个由两个质量、两个弹簧和两个阻尼 C: 器构成的二自由度振动系统，今要求在给定初始位置和 初始速度下的运动。 解：设x1和x2分别表示两个质量关于它们平衡位 图7-8两自由度机械振动模 置的偏移，则此二自由度振动系统的一般方程为： 6

第 2 章 时域中的离散信号和系统 ·6· 6 2 1 2 1 2 2 2 2 213 2 3 2 2 3 2 o c o d x m kx kx dt d x m kx kx kx dt d x m kx kx dt = − + = − + + = − 设三个原子沿轴向的振动具有同样的频率 ω， i t j j x A e  = ，则代入上式后得到： 2 1 1 2 o o k k A A A m m − = − +  2 2 2 1 3 2 c c c k k k A A A A m m m − = − + +  2 3 2 3 o o k k A A A m m − = −  写成矩阵形式为： 2 2 1 2 1 2 2 1 2 3 2 3 2 2 2 3 0 0 2 2 0 0 0 o o o o c c c c c c o o o o k k k k A A m m m m A k k k k k k A A A A m m m m m m A k k k k A A m m m m                  − − = − −                      − + − − = − − − =                             − + − = − −                O 振动的频率的平方就决定于这个系数矩阵的特征值，因为有三个特征值，要取其中的最大 值。由此写出计算程序 pla706，核心语句为： k=14.2e2, mo=16*1.6605e-27, mc=12*1.6605e-27, A=[k/mo,-k/mo,0;-k/mc,2*k/mc,-k/mc;0,-k/mo,k/mo], [x,y]=eig(A), omega=sqrt(y) lamda=2*pi*3*10^8./max(max(omega)) 其运行结果如下。答案为： omega = 1.0e+014 及 lamda = 4.257951e-006 m ≈ 4.3μm 7.7 二自由度机械振动 图 7-9 表示了一个由两个质量、两个弹簧和两个阻尼 器构成的二自由度振动系统，今要求在给定初始位置和 初始速度下的运动。 解：设 x1 和 x2 分别表示两个质量关于它们平衡位 置的偏移，则此二自由度振动系统的一般方程为： 图 7-8 两自由度机械振动模型 图 7-5 CO2分子振动结构

第2章时域中羽离散信号和系统 m元+(G+C2)元-C2元2+(k+k2)x,-k2x2=0 (7.10.1) m+C2(3-元)+k(3-x)=0 可写成矩阵形式： M成+CX+KX=0 (7.10.2 其中 M=m07 c=9+- K=+水- 0 m L-c C2 -k (7.10.4) k x 这是一个四阶的常系数齐次微分方程组，给定其初始位置X和初始速度X: [-- (7.10.4) 引进符号是为了在MATLAB编程中给导数以变量名的需要。用解析法求这个方程的解 非常麻烦，只有当C-心，即无阻尼时，系统可解耦为两种独立的振动模态，通常书上只给出解 耦简化后的解。 有了MATLAB工具，根本无需设C=0,也无需解耦，就可以用很简洁的程序求出其数值 解。其基本思路是把原始非常化成典型的四个一阶方程构成的状态方程组： Y=AY 7.10.5 这个方程在初始条件Y=Y,下的解为Y=Y,et。用MATLAB表示为Y=YO*expm(A*) 其中xpm表示把(A*)看成矩阵来求其指数。已经知道标量x求指数的方法，求矩阵指数虽然 要麻烦 些，但概念是相仿的。我们不必都弄清细节。MATLAB提供了cxpm,expml,…等多种 函数供用户调用。所以我们只要把Y,Y0和A找到就行。 先把方程(2)写成两个一阶矩阵方程： X=X 「0IX x=X=-MICX,-MIKX-MIK -.] (7.10.6 F是 A 0 L -M\K (7.10.7) 对于本题的二自由度系统，X= ]C,-]微vw题4 由于A中的四个元素都是2×2方阵，A是4×4方阵。对于更多自由度的系统，公式(7)都是正 确的 下面给出二自由度系统的一个数值例，设m1=1;m2=9:k1=4,k2=2:c1和c2可由用户输入。 求在初始条件x0=【1;0]和xd0=[0;-1]下，系统的输出x1,2曲线。 根据上面的模型可以写出程序pa710,运行此程序，输入c1-0.2,2-0.5所得的结果见图7-9。 从中可清楚地看到振动的两种模态。特别是x的运动反映了两种模态的迭合。给出不同的初始 条件，各模态的幅度也会变化。输入C1=0.c2=0所得的结果见图7-10，这时两种振动模态是可 7

第 2 章 时域中的离散信号和系统 ·7· 7 1 1 1 2 1 2 2 1 2 1 2 2 2 2 2 2 1 2 2 1 ( ) ( ) 0 ( ) ( ) 0 m x c c x c x k k x k x m x c x x k x x + + − + + − = + − + − = (7.10.1) 可写成矩阵形式： MX + CX + KX = 0 (7.10.2) 其中 1 1 2 2 1 2 2 1 1 2 2 2 2 2 0 , , , 0 m c c c k k k x m c c k k x         + − + − = = =                 − − M = C K X (7.10.4) 这是一个四阶的常系数齐次微分方程组，给定其初始位置 X0 和初始速度 Xd0： 10 10 1 0 0 0 0 20 20 2 0 , d d d x x x x x x       = = = =             X X X (7.10.4) 引进符号 xd是为了在 MATLAB 编程中给导数以变量名的需要。用解析法求这个方程的解 非常麻烦，只有当 C=0，即无阻尼时，系统可解耦为两种独立的振动模态，通常书上只给出解 耦简化后的解。 有了 MATLAB 工具，根本无需设 C＝0，也无需解耦，就可以用很简洁的程序求出其数值 解。其基本思路是把原始非常化成典型的四个一阶方程构成的状态方程组： Y = AY (7.10.5) 这个方程在初始条件 Y=Y0 下的解为 A t Y = Y e0 。用 MATLAB 表示为 Y=Y0*expm(A*t)。 其中 expm 表示把(A*t)看成矩阵来求其指数。已经知道标量 x 求指数的方法，求矩阵指数虽然 要麻烦一些，但概念是相仿的。我们不必都弄清细节。MATLAB 提供了 expm, expm1, …等多种 函数供用户调用。所以我们只要把 Y,Y0 和 A 找到就行。 先把方程（2）写成两个一阶矩阵方程：                      d d d d d X = X X X 0 I = X = X = -M \ CX - M \ KX X -M \ K - M \ C X (7.10.6) 于是                   0 0 d d0 X X 0 I Y = , Y = , A = X X - M \ K - M \ C (7.10.7) 对于本题的二自由度系统， 1 1 2 2 d d x x x x     = =         X X 和 d ，所以 Y 和 Y0 都是 4×1 的单列变量； 由于 A 中的四个元素都是 2×2 方阵，A 是 4×4 方阵。对于更多自由度的系统，公式(7)都是正 确的。 下面给出二自由度系统的一个数值例，设 m1=1; m2=9; k1 = 4; k2=2; c1 和 c2 可由用户输入。 求在初始条件 x0 = [1;0]和 xd0 = [0;-1]下，系统的输出 x1,x2 曲线。 根据上面的模型可以写出程序 pla710，运行此程序，输入 c1=0.2,c2=0.5 所得的结果见图 7-9。 从中可清楚地看到振动的两种模态。特别是 x1 的运动反映了两种模态的迭合。给出不同的初始 条件，各模态的幅度也会变化。输入 c1=0,c2=0 所得的结果见图 7-10，这时两种振动模态是可

第2章时域中]离散信号和系统 10 15 10 10 15 20 图79二自由度振动的输出波形 c1=02,c2-0.8 图7-10 二自由度振动波形cl=c2=0 解耦的。可以看出，用计算机解题时，问题和数据的复杂性对解题的过程并无根本影响。通常 我们选择比较简单，且有解析解的数据作为检验程序之用。一旦确定程序正确，它就可用在很 复杂的情况。例如作者就曾把b本例题的核心语句用在一个五自由度的系统上，解一个十阶的 线性方程组，同样得出满意的结果。 7.8FR数字滤波器最优化设计H12 设给定滤波器的预期幅频特性D(⊙)在o=ω，(1,2…)的K个频点上的值，若实际滤 波器的脉冲响应的长度为N-2L+1,则其幅特性与预期特性相拟合的方程为： A()=>d(n)cosno =D(@:)=D: (白1.2..，0 这K个方程联立。由于4@)是L+l个谐波的线性组合，这方程组中的待定参数d)》 有L+1个。 如果K=L+1,即方程数与未知数的数目相等，则这个线性方程组是适定的，恰好可以 解了这些系数。 如果>L+1,即方程数比未知数的数目多，形成了所谓超定方程组。那就不可能找到 精确满足这些方程组的系数山，只能找到最近似地满足这些方程的最小二乘解。 如果K<L+1,则形成了不定方程组，那会有无穷个解，工程上是没有意义的。所以只 考虑K≥L+1的情况。 npd 其中：e为单列K元误差向量，D为预期幅特性在样本点列上的K元单列向量，d为 L+1元待定系数单列向量，而P则是由cos(nw,)组成的K×(L+1)的系数矩阵。 e D 「1cos(M)·cos(Lm)1 do e-i 1cos()… cos(Lo) d= L1cos(Ok）·cos(LOx) 前面已经得到它的最小二乘解的公式： 8

第 2 章 时域中的离散信号和系统 ·8· 8 解耦的。可以看出，用计算机解题时，问题和数据的复杂性对解题的过程并无根本影响。通常 我们选择比较简单，且有解析解的数据作为检验程序之用。一旦确定程序正确，它就可用在很 复杂的情况。例如作者就曾把 b 本例题的核心语句用在一个五自由度的系统上，解一个十阶的 线性方程组，同样得出满意的结果。 7.8 FIR 数字滤波器最优化设计[12] 设给定滤波器的预期幅频特性 D(ω)在ω=ωi(i=1,2,…,K)的 K 个频点上的值，若实际滤 波器的脉冲响应的长度为 N=2L+1，则其幅特性与预期特性相拟合的方程为： 0 ( ) ( )cos ( ) L i i i i n A d n n D D    = = = =  (i=1, 2, …, K) 这 K 个方程联立。由于 A( ) i 是 L+1 个谐波的线性组合，这方程组中的待定参数 d(n) 有 L+1 个。 如果 K=L+1，即方程数与未知数的数目相等，则这个线性方程组是适定的，恰好可以 解了这些系数。 如果 K>L+1，即方程数比未知数的数目多，形成了所谓超定方程组。那就不可能找到 精确满足这些方程组的系数 d(n)，只能找到最近似地满足这些方程的最小二乘解。 如果 K<L+1，则形成了不定方程组，那会有无穷个解，工程上是没有意义的。所以只 考虑 K≥L+1 的情况。 e=D−Pd 其中：e 为单列 K 元误差向量，D 为预期幅特性在样本点列上的 K 元单列向量，d 为 L+1 元待定系数单列向量，而 P 则是由 cos（nωi）组成的 K(L+1)的系数矩阵。 1 1 1 1 0 2 2 2 2 1 1 cos( ) cos( 1 cos( ) cos( , , , 1 cos( ) cos( K K K K L e D L d e D L d e D L d                       = = = =                                 e D P d ） ） ） 前面已经得到它的最小二乘解的公式： 图 7-9 二自由度振动的输出波形 c1=0.2，c2=0.8 图 7-10 振动的输出波形(c1=c2=0) 图 7-10 二自由度振动波形 c1=c2=0

第2章时域中的离散信号和系统 d=(PTP)PTD 用MATLAB计算此式特别方便，可以表示为上iv(P*P)P*D,也可以更简便地 用左除运算d=PD来完成。 例7.8举一个数字例，要求设计长度为N=9(有5个待定系数)的FR滤波器，要使 它在0~π之间的八个频点。上逼近预期的低通幅特性D: w=0,0.33,0.67,1,1.5,2,2.5,3.141D=1,1,1,1,0.00.0 解：列出方程组的完整形式： D c092c0s30 d0 1 cos cos2@cos30 cos4c d 三P*d=D 1 coses cos2s cos3os cos4o dB) 1 cose cos2 cos30 cos4m d4) 1 coseh cos2oh cos3 cos40 1 coss cos20s cos30s cos4e 看来系数矩阵P的赋值比较麻烦，其实，回想求离散傅里叶变换时的做法，可以利用 列矩阵w'=;份，；w网乘行矩阵0：4形成 一个85矩阵，然后求余弦得到P。这可以用 MATLAB语句P-cos(w'0:4])轻而易举地列出。因此用下列几行MATLAB程序agl010就 可以方便地完成最小二乘最优滤波器的设计。 W=9:1=f1o0r（N-1)/21: s列出待求系数字数 ,020o0d6522.53.1 0 p-o 多列出P矩 d=inv(e*p)+p'知 器求出待求系留 程序运行的结果为 知道)以后，就可以计算滤波器的频 率特性进行校核。得到的幅频特性见图 0.s 7-1山。因为L=4,最高的谐波次数为4，在 0~π之间幅特性摆动最多两个周期，达到 峰值的次数应为四次，这从图上也看得很 清楚。 图7-11设计出的最优化滤波器的顿率特性 7.9弹性梁的柔度矩阵 设简支梁如图7-12所示，在梁的三个位置分别施加力6,6和6后，在该处 产生的综合变形为图示的y 2和，通常称为挠度。根据虎克定律，在材料未失去弹性的范 围内，力与它引起的变形呈线性关系，可以写出完全的矩阵形式为： 9

第 2 章 时域中的离散信号和系统 ·9· 9 ( ) -1 T T d = P P P D 用 MATLAB 计算此式特别方便，可以表示为 d=inv（P’*P）*P’*D，也可以更简便地 用左除运算 d=P\D 来完成。 例 7.8 举一个数字例，要求设计长度为 N=9( 有 5 个待定系数)的 FIR 滤波器，要使 它在 0～π 之间的八个频点ω上逼近预期的低通幅特性 D： ω=[0, 0.33, 0.67, 1, 1.5, 2, 2.5, 3.14]; D=[1,1,1,1,0,0,0,0]; 解：列出方程组的完整形式： 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5 6 6 6 6 7 7 7 7 8 8 8 1 cos cos 2 cos3 cos 4 1 cos cos 2 cos3 cos 4 1 cos cos 2 cos3 cos 4 1 cos cos 2 cos3 cos 4 1 cos cos 2 cos3 cos 4 1 cos cos 2 cos3 cos 4 1 cos cos 2 cos3 cos 4 1 cos cos 2 cos3 cos 4                                 1 2 3 4 5 6 7 8 8 (0) (1) (2) * (3) (4) D D d D d D d D d D d D D                 =              P d = D 看来系数矩阵 P 的赋值比较麻烦，其实，回想求离散傅里叶变换时的做法，可以利用 列矩阵 w’=[w1; w2; …; w8]乘行矩阵[0:4]形成一个 85 矩阵，然后求余弦得到 P。这可以用 MATLAB 语句 P=cos(w’*[0:4])轻而易举地列出。因此用下列几行 MATLAB 程序 ag1010 就 可以方便地完成最小二乘最优滤波器的设计。 N=9; L=floor((N-1)/2); % 列出待求系数序数 w=[0,0.33,0.67,1,1.5,2,2.5,3.14]; % 列出频率向量 D=[1,1,1,1,0,0,0,0]; % 列出预期幅特性向量 P=cos(w’*[0:L]); % 列出 P 矩阵 d=inv(P'*P)*P'*D’ % 求出待求系数 程序运行的结果为 d = 0.3981 0.6039 0.2137 -0.1205 -0.1506 知道 d(n)以后，就可以计算滤波器的频 率特性进行校核。得到的幅频特性见图 7-11。因为 L=4，最高的谐波次数为 4，在 0～π 之间幅特性摆动最多两个周期，达到 峰值的次数应为四次，这从图上也看得很 清楚。 7.9 弹性梁的柔度矩阵 设简支梁如图 7-12 所示，在梁的三个位置分别施加力 f1，f2 和 f3 后，在该处 产生的综合变形为图示的 y1，y2 和 y3，通常称为挠度。根据虎克定律，在材料未失去弹性的范 围内，力与它引起的变形呈线性关系，可以写出完全的矩阵形式为： 图 7-11 设计出的最优化滤波器的频率特性