
西安电子科枝大学 电子工程学院《A School of Electronic Engineering.Xidian University http: xidian.edu.cn edu.ci 场论与复变函数 exu(①miox 主讲:徐乐 2011年11月6日星期
lexu@mail.xidian.edu.cn

内容提要 ■课程的教学目标与任务 du 。掌握场论的有关内容、概念和方法,使学生理解和掌 握在力学、电学、电磁学等学科中所遇到的场的数学 背景,掌握其运算的一般规律,使学生得到抽象科学 思维的训练,提高学生数学素养和能力,为学生学习 有关后续课程以及进步扩大数学知识奠定必要的数 学基础。 ·本课程与其它课程的联系和分王 ·场论是工科类专业学生的必修课程,它揭示和探索了 某种物理量(如:温度、密度、电位、力、速度等等)空 间的分布和变化率,是现代化科学中不可缺少的数学 工具 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

内容提要 场论(10学时) du.C ·数量场和矢量场的概念;数量场的等值面和矢量场的矢量线的概 念 。数量场的方向导数和梯度的定义及计算: 。矢量场的通量和散度的定义及计算;矢量场的管量和旋度的定义 及计算: 。有势场、管形场、调和场的概念和意义。 ■重点、难点 。重点:数量场、矢量场的基本概念,方向导数和梯度、通量和散 度、环量和旋度的计算。 ·难点:方向导数和梯度、通量和散度、环量和旋度的计算、哈密 顿算子的应用。 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

内容提要 ■基本要求 。正确理解数量场、矢量场的基本概念,理解数量场的等值面和矢 量场的矢量线的意义。 正确理解数量场的方向导数及梯度的概念,并会求一般函数沿给 定方向的方向导数和梯度。 。正确理解矢量场的通量及散度的意义,熟练运用法则求一些矢量 场的通量和散度。 ·正确理解矢量场的环量及旋度的意义,会用基本公式求一些矢量 场的环量和旋度。 ● 理解有势场、管形场、调和场的基本概念,会求有势场的势函数: 理解矢性算子(哈密顿算子)的一般概念。 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
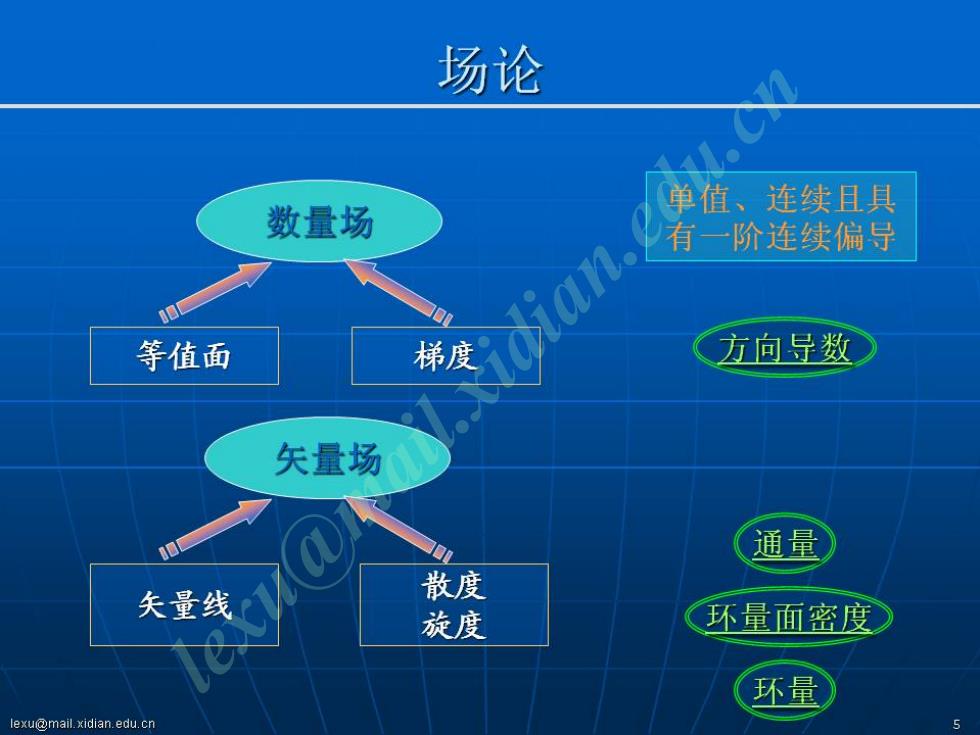
场论 单值、连续且具 数量场 0 等值面 梯度 iau. 一阶连续偏导 方向导数 矢量场 通量 矢量线 e 散度 旋度 环量面密度 环量 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

特殊矢量场 有势场 A=grad u 4=-gradv rotA =0 u(x,y,2)= Px+∫+∫Rxyz)止 ·管形场 diA≡0 )d=-R(.y.)dy 4=rotB v=∫Pxy)d W=C(C为任何常数) ·调和场 div 0 xy)=-P(xy)-∫xy)d rot4=0 ex ux=∫-Q(xyk+∫P(xy)d lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
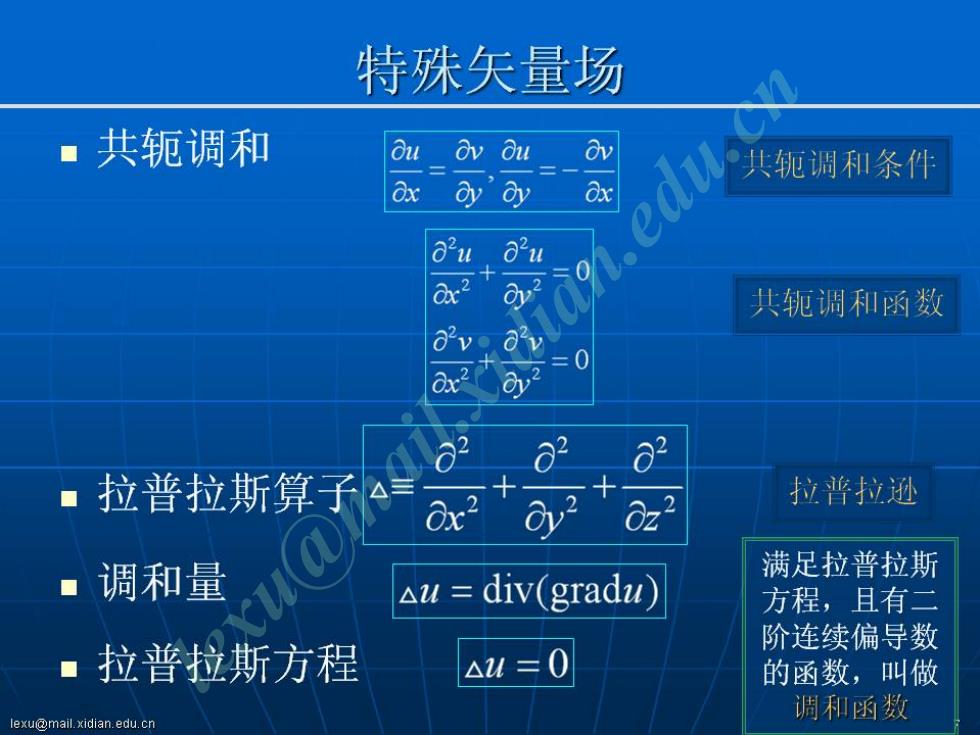
特殊矢量场 ·共轭调和 Ou Ov Ou edu. 轭调和条件 Cx? 共轭调和函数 O've 0'v =0 2 拉普拉斯算子 拉普拉逊 0z2 调和量 满足拉普拉斯 △u=div(gradu) 方程,且有二 阶连续偏导数 拉普拉斯方程 △2u=0 的函数,叫做 调和函数 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
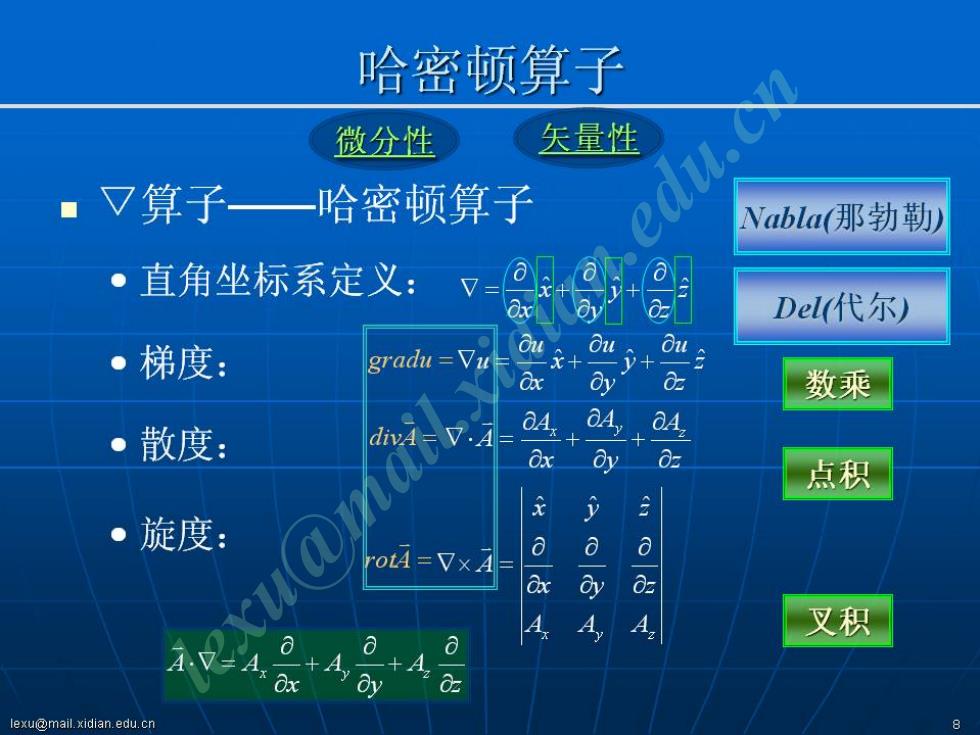
哈密顿算子 微分性 矢量性 。V算子一哈密顿算子 Nablat(那勃勒) 。直角坐标系定义:又 Del代尔) 。梯度: gradu Vu Ou V+ d 数乘 。散度: divA-V.A OA Ov 0 点积 ·旋度: A A 叉积 AV-4.7 Ay oy _tA: lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

哈密顿算子 。两个矢量恒等式 edu.Cx div(rot4)=0 V:(N×A④=0 旋无散 rot(gradu)=0 梯无旋 两个积分变换 线面 divAdv A.=vA 面→体 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

正交曲线坐标系 拉梅系数 du. 。坐标曲线弧微分ds=土√d2中2+d 拉梅系数 ds,=H,dg, H. )+必+) ag,0q. aq 般曲线的弧微分 ds"ds,"+ds,"ds Hdg,"+H2"dq."+H"'dqs"dx"+dy+d" exu(a lexu@mail.xidian.edu.cn 10
lexu@mail.xidian.edu.cn