
西安电子科枝大学 电子工程学院《A School of Electronic Engineering.Xidian University http:/ .xidian.edu.cn edu.cr 场论与复变函数 xuamail.x 主讲:徐乐 2011年11月6日星期日
lexu@mail.xidian.edu.cn

Review dw 复变函数的导数f()= lim (+正)-f(】 △ ·实变函数的求导法则可适用于复变函数,且证 法相同 复变函数的微分△w=了()+p)A ·f)△z为函数在w=∫包)点z的微分 解析函数 ·[定义]若函数f包)在zo及zo的邻域内处处可导, Q则称函数/6在:,解近 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复变函数的导数 ■若w=fE)=u(,以+iv(x,y,(x,)∈D,则 有极限 有极限 u=u(x,y) w=fE)在zo 连续 连续 v=Vx,以 X 可导 可导 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

解析函数 定理1):f包)、g)在区域D解析0则其四则运算 (除去分母为零的点外的商)在D内解析 定理2):复合函数的解析性质: ·设函数h=g回)在z平面上的区域D内解析 ·设函数w=f)在h平面上的区域G内解析 ·若对D内每一点2o,函数g)对应值都属于G,则复合 函数w=f[g]在D内解析 ex lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
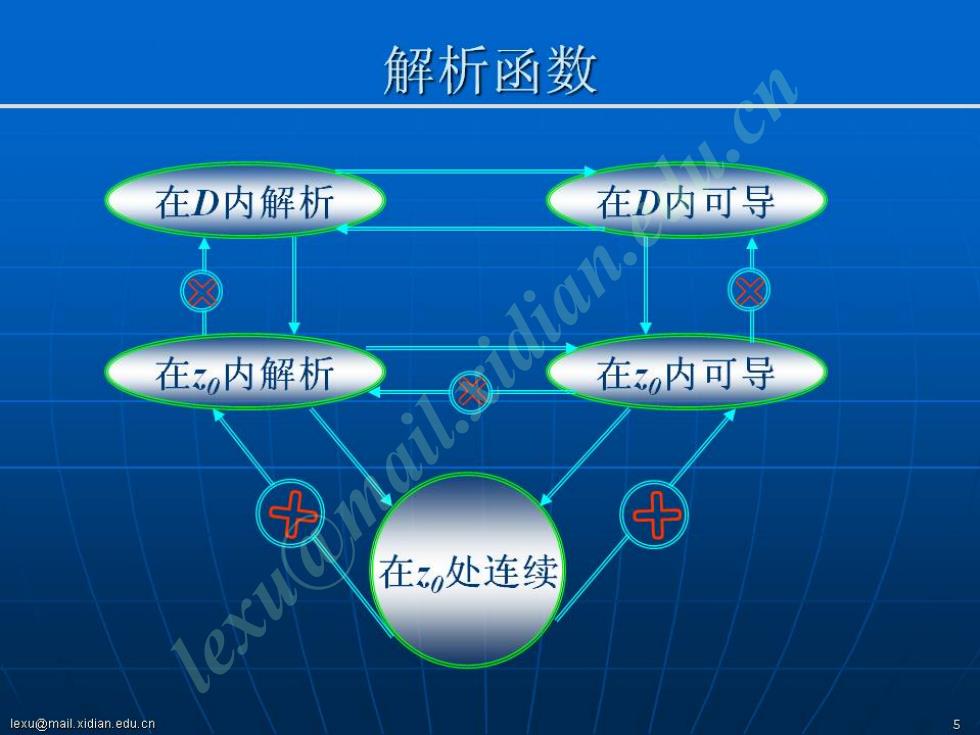
解析函数 在D内解析 在D内可导 lian- 在内解析 在30内可导 exu 在z处连续 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

解析函数 ■[思考]若函数w=f回=4)十i()可导 u(x)、vx,y)有什么性质?心 ·函数w=fe)=(c,)十ix)在区域D内一点z=x+y可导的必 要条件 ou Ov Cauchy-Riemann方程 成 柯西-黎曼方程 Bu o lexu(a Bx lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

解析函数 ■定理一复变函数在一点处可导的充要条件 ·函数fe=u()+ivx)在区域D内 ·函数f②在D内一点z=x+可导的充要条件 u(x,y)和v(xy)在点(x,)可微 ■且在该点满足柯西-黎曼方程 Ov ou Ov a战 ay ay Bx 必要性已证,充分性有待证明 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

lexu@mail.xidian.edu.Cn 第10讲解析函数(Ⅱ) 解析函数的充要条件 平面场的复势 lexu@mail.xidian.edu.cn 8
lexu@mail.xidian.edu.cn

解析函数的充要条件 可导函数的充要条件 du. ·定理一复变函数在一点处可导的充要条件 ■函数f)=cy)+i(x,)在区域D内 ■函数f)在D内一点zx+y可导的充要条件 ·uc,y)和v(x,y)在点(x,y)可微 。且在该点满足柯西-黎曼方程 Bu Ov Ou exu 0'a Ex 必要性已证,充分性有待证明 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

解析函数的充要条件 [充分性] f(z+△z)-f(z) =u(x+△x,y+△y)-u(x,y)+v(x+△x,y+△y)-(x,y)] =△u+i△y △= Ay+&Ax+EAy u(,y)和 8=0 4x0 在点()可微 Ov △y0 △y+6△x+8,Ay C-R u)y Ox 条件 ax ay ay Ox +(s+is3)Ax+(62+i)Ay f(z+△c)-f(z)=( +X牛+G+应平G+运 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn