
SIT 复变函数与场论 主讲:徐乐
复变函数与场论 主讲:徐乐
第22讲 共形映射 必共形映射 ·解析函数导数的几何含义 ■共形映射的概念 分式线性映射 ·保角性 ■保圆性 ·保对称性 ·唯一决定分式线形映射的条件 lexu@mail.xidian.edu.cn F&C
lexu@mail.xidian.edu.cn F&C 2 第22讲 共形映射 共形映射 解析函数导数的几何含义 共形映射的概念 分式线性映射 保角性 保圆性 保对称性 唯一决定分式线形映射的条件
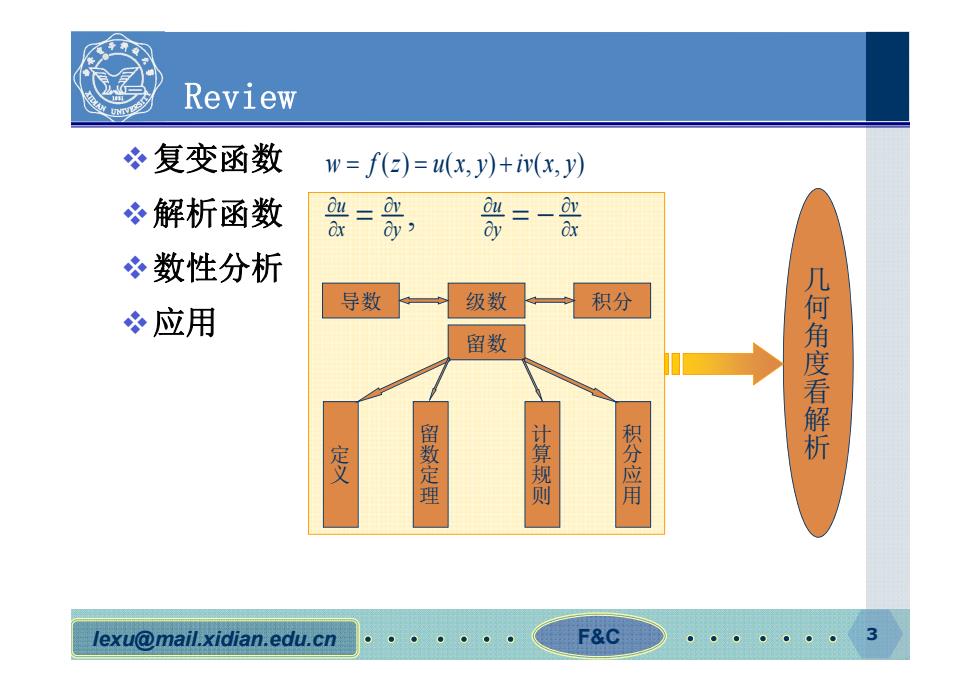
Review 复变函数 w=f(2)=u(x,y)+iv(x,y) 解析函数 dy> 必=- a 数性分析 导数 级数 积分 冬应用 留数 几何角度看解析 留数定理 计算规则 积分应用 lexu@mail.xidian.edu.cn F&C
lexu@mail.xidian.edu.cn F&C 3 Review 复变函数 解析函数 数性分析 应用 w f z u x y iv x y () (, ) (, ) , uv u v xy y x 导数 级数 积分 留数 定义 留数定理 计算规则 积分应用 几何角度看解析

共形映射 §1、背景 映射:将复杂区域转化到简单区域求解。 共形映射是复变函数论中最重要的概念之一,与 物理中的概念有密切的联系,而且对物理学中许 多领域有重要的应用。 ·应用共形映射成功地解决了流体力学与空气动力 学、弹性力学、磁场、电场与热场理论以及其他 方面的许多实际问题。不但如此,20世纪中亚音 速及超音速飞机的研制促成了从共形映射理论到 拟共形映射理论的发展。 lexu@mail.xidian.edu.cn F&C
lexu@mail.xidian.edu.cn F&C 4 一 、 共形映射 §1、背景 映射:将复杂区域转化到简单区域求解。 共形映射是复变函数论中最重要的概念之一,与 物理中的概念有密切的联系,而且对物理学中许 多领域有重要的应用。 应用共形映射成功地解决了流体力学与空气动力 学、弹性力学、磁场、电场与热场理论以及其他 方面的许多实际问题。不但如此,20世纪中亚音 速及超音速飞机的研制促成了从共形映射理论到 拟共形映射理论的发展
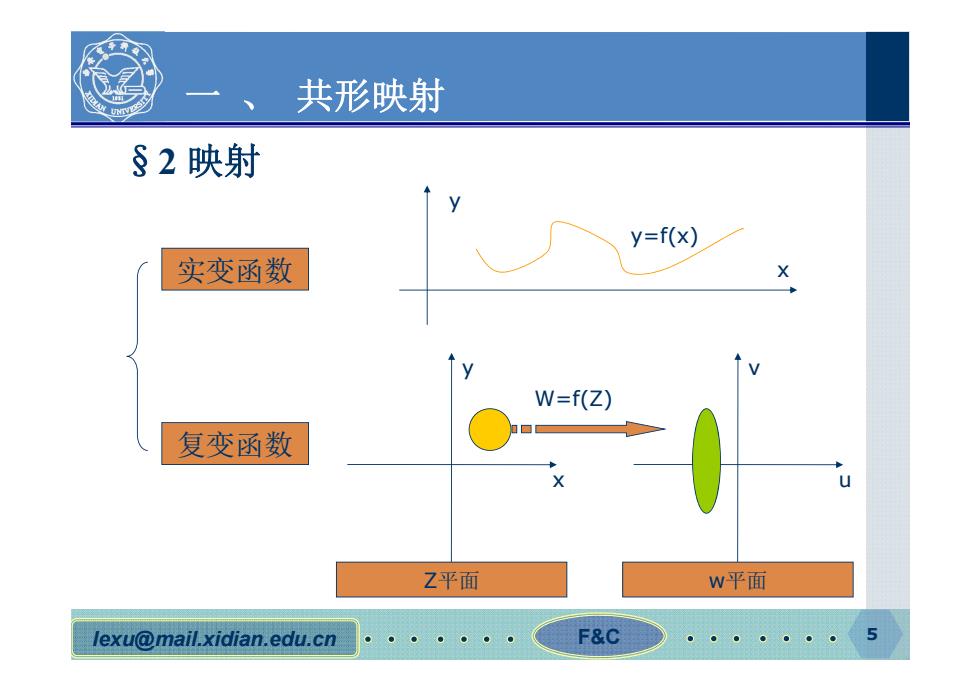
共形映射 §2映射 y=f(x) 实变函数 W=f(Z) 复变函数 Z平面 W平面 lexu@mail.xidian.edu.cn F&C 5
lexu@mail.xidian.edu.cn F&C 5 一 、 共形映射 §2 映射 实变函数 复变函数 x y y=f(x) x y Z平面 u v w平面 W=f(Z)
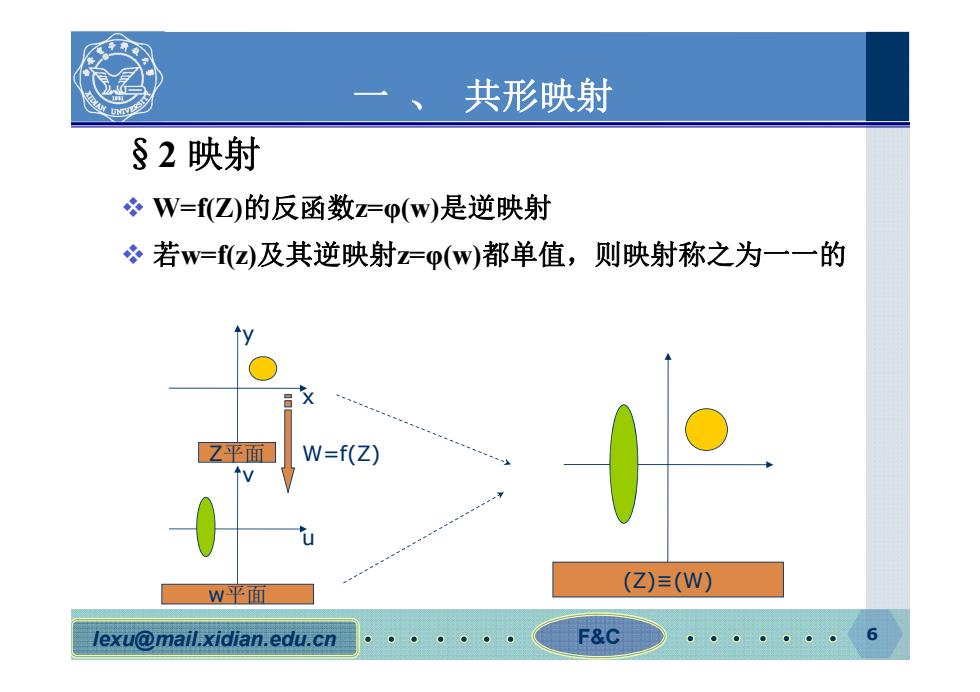
共形映射 §2映射 W=fZ)的反函数z=p(w)是逆映射 若w=z)及其逆映射z=p(w)都单值,则映射称之为一一的 Z平面 W=f(Z) W平面 (Z)≡(W) lexu@mail.xidian.edu.cn F&C 6
lexu@mail.xidian.edu.cn F&C 6 一 、 共形映射 §2 映射 W=f(Z)的反函数z=φ(w)是逆映射 若w=f(z)及其逆映射z=φ(w)都单值,则映射称之为一一的 x y Z平面 u v w平面 W=f(Z) (Z)≡(W)

一、 共形映射 必例: C1:x2-y2=1 C2:x2-y2=2 C1:u=1 C2:u=2 C3:xy=1 u+iv=(x2-y2)+i2xy C3:v=2 C4:y=2 C4:y=4 lexu@mail.xidian.edu.cn F&C
lexu@mail.xidian.edu.cn F&C 7 一、共形映射 例: 2 w z 2 2 2 2 1: 1 2: 2 3: 1 4: 2 Cx y Cx y C xy C xy 2 2 u iv x y i xy ( )2 1: 1 2: 2 3: 2 4: 4 C u C u C v C v u v x y
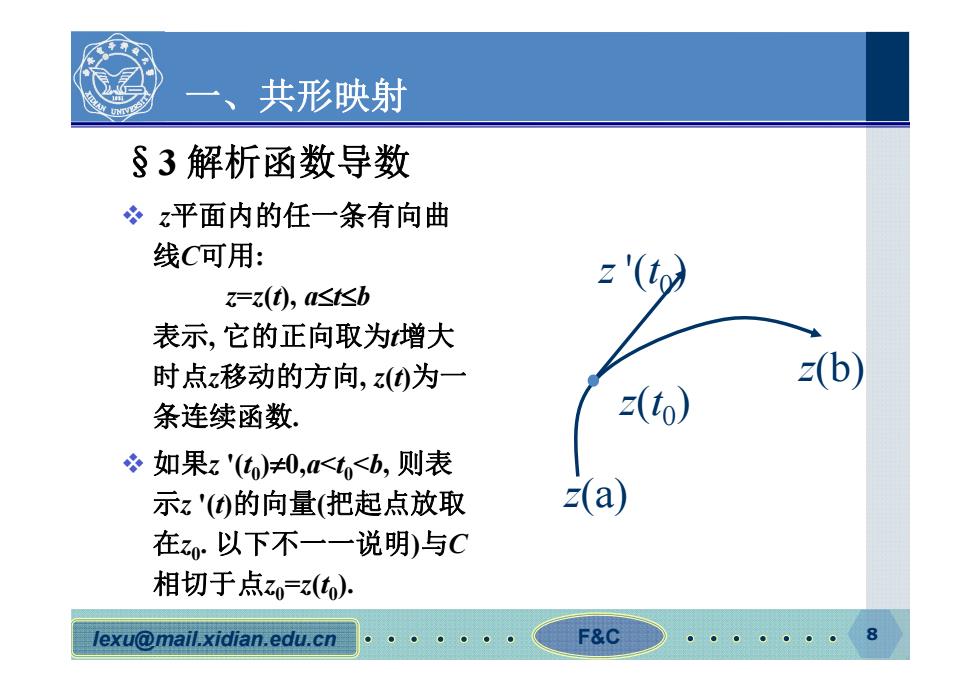
一、 共形映射 §3解析函数导数 冬z平面内的任一条有向曲 线C可用: z'( =z(),a≤b 表示,它的正向取为增大 时点x移动的方向,)为一 z(b) 条连续函数. (to) 如果z'(t)0,<<b,则表 示z'()的向量(把起点放取 (a) 在z0以下不一一说明)与C 相切于点z0=): lexu@mail.xidian.edu.cn F&C 0●1.●0 8
lexu@mail.xidian.edu.cn F&C 8 一、共形映射 §3 解析函数导数 z平面内的任一条有向曲 线C可用: z=z(t), atb 表示, 它的正向取为t增大 时点z移动的方向, z(t)为一 条连续函数. 如果z '(t0)0,a<t0<b, 则表 示z '(t)的向量(把起点放取 在z0. 以下不一一说明)与C 相切于点z0=z(t0). z(a) z(b) z(t0) z '(t0)

共形映射 事实上,如果通过C上 两点P。与P的割线PP 的正向对应于增大的 方向,则这个方向与 z(t6+△) z(t+△)-z(to) △t 表示的方向相同. (to) lexu@mail.xidian.edu.cn F&C
lexu@mail.xidian.edu.cn F&C 9 一、共形映射 事实上, 如果通过C上 两点P0与P的割线P0P 的正向对应于t增大的 方向, 则这个方向与 表示的方向相同 . t z t t z t Δ ( Δ ) ( ) 0 0 O x y P0 P z(t0) z(t0+t)C
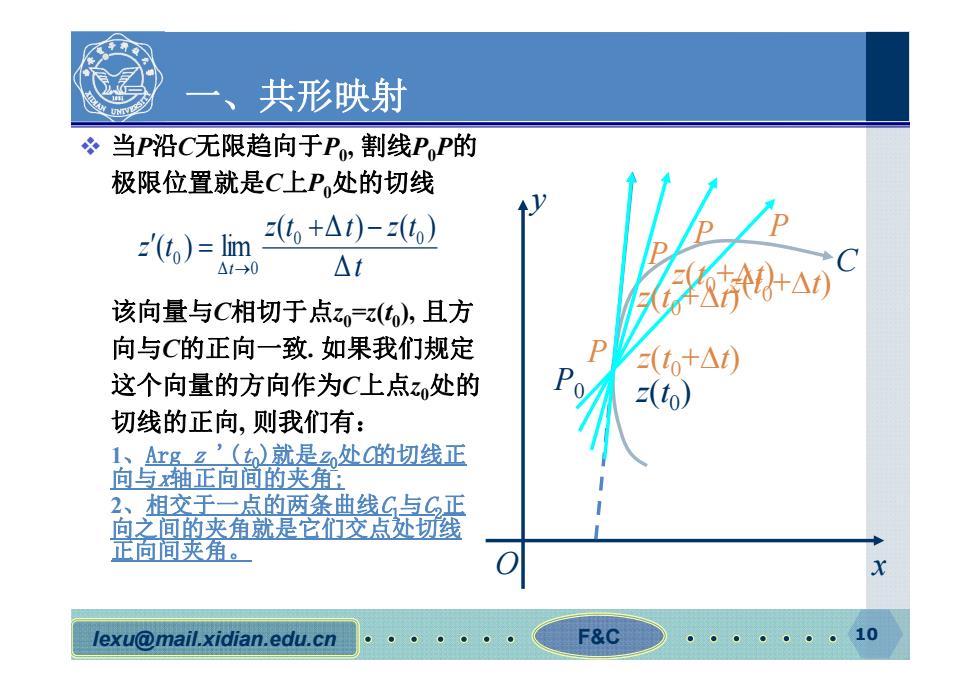
共形映射 当P沿C无限趋向于P,割线PP的 极限位置就是C上P处的切线 z(+△t)-z(to) (to)=lim △t0 △t 该向量与C相切于点z。=z),且方 向与C的正向一致.如果我们规定 (t+△) 这个向量的方向作为C上点z处的 0 z(t0) 切线的正向,则我们有: 1、Argz'(t)就是2处C的切线正 向与x轴正向间的夹角的 2、相交于一点的两条曲线C与C正 向之间的夹角就是它们交点处线 正向间夹角。 lexu@mail.xidian.edu.cn F&C 10
lexu @mail.xidian.edu.cn F&C 10 一、共形映射 当 P沿 C无限趋向于 P0, 割线 P0P 的 极限位置就是 C上 P0处的切线 该向量与 C相切于点 z 0 = z ( t0), 且方 向与 C的正向一致. 如果我们规定 这个向量的方向作为 C上点 z 0处的 切线的正向, 则我们有: 1 、Arg z '( t0)就是 z0 处 C的切线正 向与 x轴正向间的夹角; 2 、相交于一点的两条曲线 C1与 C2 正 向之间的夹角就是它们交点处切线 正向间夹角。 t z t t z t z t t Δ ( Δ ) ( ) ( ) lim 0 0 Δ 0 0 P z ( t 0 + t ) O x y P 0 z ( t 0 ) C z ( t 0 + t ) z ( t 0 + t ) z ( t 0 + t ) P P P