
1931 矩阵论 主讲教师:徐乐 2014年10月29日星期三
2014年10月29日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 冬第五讲矩阵对角化 ”内积空间 ·正规矩阵 ·酉对角化 lexu@mail.xidian.edu.cn 矩阵论 。。。。。。2
lexu@mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第五讲 矩阵对角化 内积空间 正规矩阵 酉对角化

内积空间 冬酉空间 ■设V是复线性空间(k∈C),对于V中任何两个元素x、 y均按某一规则存在一个复数与之对应,记为心,y) ·若它满足以下四个性质,则称x,y)为x与y的内积 ·定义了内积的复线性空间称为酉空间 ·(1)交换律(x,y)=(y,x) ·(2)分配律c,y+z=(c,y)+(c,) ·(3)齐次律(c,y)=kc,) (x,ky)=k(x,y) ·(4)非负性,化,x)≥0 -当且仅当=0时,(xx)=0 lexu@mail.xidian.edu.cn 矩阵论 ●●● 3
lexu@mail.xidian.edu.cn 矩 阵 论 3 内积空间 酉空间 设V是复线性空间(k∈C),对于V中任何两个元素x、 y均按某一规则存在一个复数与之对应,记为(x , y) 若它满足以下四个性质,则称(x , y)为x与y的内积 定义了内积的复线性空间称为酉空间 • (1)交换律 • (2)分配律 (x , y + z)= (x , y)+ (x , z) • (3)齐次律 (kx , y) = k (x , y) • (4)非负性 , (x , x)≥0 – 当且仅当x=0时, (x ,x)=0 ( xy yx , , ) = ( ) ( x ky k x y , , ) = ( )

内积空间 冬Gram-Schmidt正交化手续 ■设1,2,…,心n为一组线性无关的元素或向量 ·则可进行如下正交归一化操作 ·即正交规范化或正交单位化 y k21=-(x21) (x2,1)=(x2,y1)+k21y1,y1)=0 x2=x2k2y1 k31=-(x3y1) (x3,1)=(x3y1)+k31=0 =x3+k3y1+k22 k32=-(x32) (x3,y2)=(x3y2)+k32=0 3= k,=-(y) 5=(y,x) x=x,+ i=1 x=5y+52y2+…+5nyn i=1,2,…,n lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 4 内积空间 Gram-Schmidt正交化手续 设 为一组线性无关的元素或向量 则可进行如下正交归一化操作 1 • 即正交规范化或正交单位化 1 1 | | x y x = 2 2 21 1 x x ky ′ = + 2 1 2 1 21 1 1 k xy 21 2 1 = −(,) (,)(,) (,)0 xy xy k yy ′ =+ = 2 2 2 | | x y x ′ = ′ 3 3 31 1 32 2 x x ky ky ′ =+ + 3 1 3 1 31 (,)(,) 0 xy xy k ′ = += 3 2 3 2 32 (,)(,) 0 xy xy k ′ = += ( ) ( ) 31 3 1 32 3 2 , , k xy k xy = − = − 3 3 3 | | x y x ′ = ′ 1 1 i i i ij j j x x ky − = k xy ij i j = −( , ) ′ = + ∑ | | i i i x y x ′ = ′ . . 11 2 2 n n xy y y = + ++ ξξ ξ ( ,) i i ξ = y x
正规矩阵 冬实对称矩阵与厄米矩阵 ·实对称矩阵 A"=A ·厄米矩阵 4"=A 实矩阵 ·实反对称矩阵 A"=-A 复矩阵 ·反厄米矩阵 A"=-A 正交矩阵和酉矩阵 ■正交矩阵ATA=AAT=I ·酉矩阵 AA=AA=I lexu@mail.xidian.edu.cn 矩阵论 5
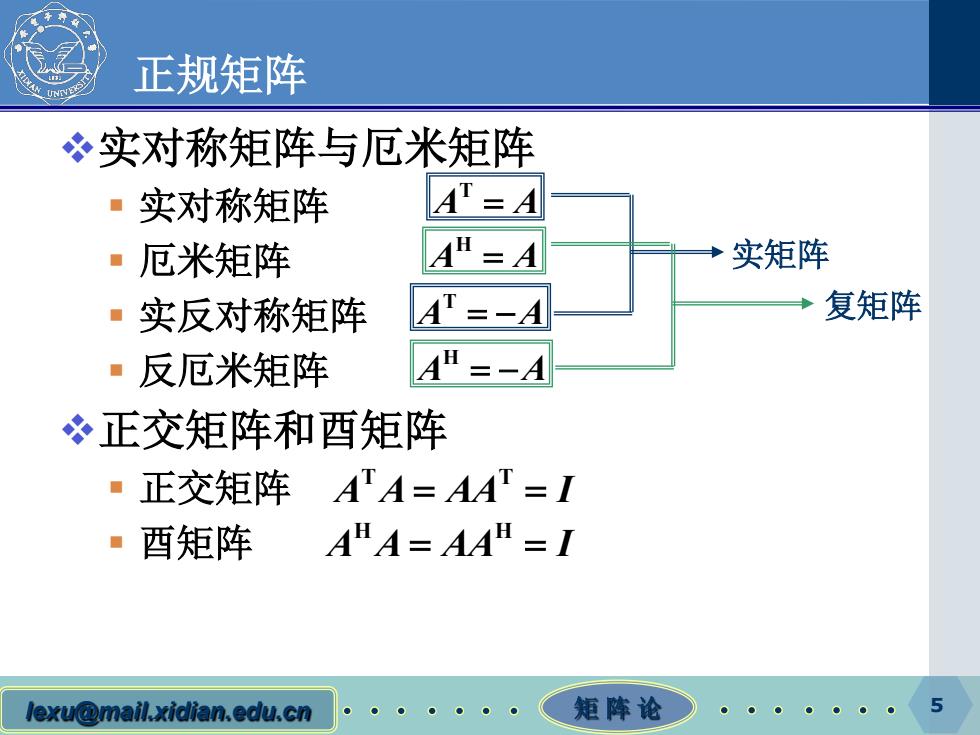
lexu@mail.xidian.edu.cn 矩 阵 论 5 正规矩阵 实对称矩阵与厄米矩阵 实对称矩阵 厄米矩阵 实反对称矩阵 反厄米矩阵 正交矩阵和酉矩阵 正交矩阵 酉矩阵 T A A = H A A = T A A = − H A A = − 实矩阵 复矩阵 T T A A AA I = = H H A A AA I = =

正规矩阵 冬正规矩阵 ·实矩阵A ·若满足ATA=AAT,则A为实正规矩阵 ·复矩阵A ·若满足AHA=AAH,则A为复正规矩阵 ■显然 ·实对称矩阵、实反对称矩阵、正交矩阵均为实正规 矩阵 ·厄米矩阵、反厄米矩阵、酉矩阵均为复正规矩阵 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 6 正规矩阵 正规矩阵 实矩阵A • 若满足ATA = AAT ,则A为实正规矩阵 复矩阵A • 若满足AHA = AAH ,则A为复正规矩阵 显然 • 实对称矩阵、实反对称矩阵、正交矩阵均为实正规 矩阵 • 厄米矩阵、反厄米矩阵、酉矩阵均为复正规矩阵

酉对角化 冬Schur引理 ·设元,2,…,2n是n阶方阵A的特征值 ·则存在酉矩阵U,使 米 U-AU- 22 0 lexu@mail.xidian.edu.cn ●1 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 7 酉对角化 Schur引理 设 是 n 阶方阵 A 的特征值 则存在酉矩阵U,使 λ λ λ n , , , 1 2 ∗ = − n U AU λ λ λ 0 2 1 1

第5讲Jordan标准形 冬酉对角化充要条件 冬Jordan标准形 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 8 第5讲 Jordan标准形 酉对角化充要条件 Jordan标准形

酉对角化充要条件 必定理 ·阶方阵A,酉相似于对角阵的充要条件是 ·A为正规阵(实或复) ·不能酉对角化的矩阵仍有可能采用其它可逆变换将 其对角化 ·实正规矩阵一般不能通过正交相似变换对角化。 (若特征值全为实数,则可正交相似对角化) lexu@mail.xidian.edu.cn 矩阵论 ●●
lexu@mail.xidian.edu.cn 矩 阵 论 9 酉对角化充要条件 定理 n阶方阵A,酉相似于对角阵的充要条件是 A为正规阵(实或复) • 不能酉对角化的矩阵仍有可能采用其它可逆变换将 其对角化 • 实正规矩阵一般不能通过正交相似变换对角化。 (若特征值全为实数,则可正交相似对角化)

酉对角化充要条件 冬定理 "阶方阵A,酉相似于对角阵的充要条件是 ·A为正规阵(实或复) ·[证明 ·由Schuri引理,存在酉矩阵U使得 A=URAU= 1≤i≤ji≤n 11,22,,几n是A的特征值 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 10 酉对角化充要条件 定理 n阶方阵A,酉相似于对角阵的充要条件是 A为正规阵(实或复) • [证明] • 由Schur引理,存在酉矩阵U使得