西安电子科技大学：《矩阵论》研究生课程教学课件（讲义，2014）10 矩阵三角分解

矩阵论 主讲教师：徐乐 2014年12月10日星期三

2014年12月10日星期三 矩 阵 论 主讲教师：徐乐

上讲回顾 冬第10讲矩阵函数及其微积分 ·矩阵函数的另外一种计算方法 ·利用零化多项式计算矩阵函数 ·矩阵微分方程 ·矩阵的微分和积分 ·一阶线性齐次常系数微分方程组 ·一阶线性非齐次常系数微分方程组 lexu@mail.xidian.edu.cn 矩阵论→

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第10讲 矩阵函数及其微积分  矩阵函数的另外一种计算方法 • 利用零化多项式计算矩阵函数  矩阵微分方程 • 矩阵的微分和积分 • 一阶线性齐次常系数微分方程组 • 一阶线性非齐次常系数微分方程组

利用零化多项式求解矩阵函数 冬根据最小多项式求矩阵函数的一般方法 ·求出最小多项式 9,2)=d.)=(--…(2-)严，m=m ·形式上写出待定多项式 ga)=2c=c,+c2+c2+…+cn2 ·求解关于待定系数的线性方程组 g(2)=f(2)(k=1,2,…,m;i=1,2,…,r) ·求出g(A),即可得f(A)=g(A) lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 利用零化多项式求解矩阵函数 根据最小多项式求矩阵函数的一般方法  求出最小多项式  形式上写出待定多项式  求解关于待定系数的线性方程组  1 2 0 12 1 () () ( )( ) ( ) , r r mm m n ri i         d mm         1 2 1 01 2 1 0 ( ) m i m i m i g c cc c c              

矩阵的微分和积分 冬矩阵导数定义 ·若矩阵A()=(a)mxn的每一个元素a)是变量 t的可微函数，则称A(可微 ·其导数定义为 dA dt =A'()= dog dt /mxn ·类似地，可以定义矩阵高阶导数以及偏导数 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 矩阵的微分和积分 矩阵导数定义  若矩阵A(t)=(ai,j(t))m×n的每一个元素ai,j(t)是变量 t的可微函数，则称A(t)可微  其导数定义为  类似地，可以定义矩阵高阶导数以及偏导数 ( ) ij m n dA da A t dt dt          

矩阵的微分和积分 矩阵积分定义 ·若矩阵A(=(a)mxn的每一个元素a都是区 间[t,t上的可积函数，则称A()在区间[o,上 可积 ·定义A()在t,]上的积分为 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 矩阵的微分和积分 矩阵积分定义  若矩阵A(t)=(ai,j(t))m×n的每一个元素ai,j(t)都是区 间[t0,t1]上的可积函数，则称A(t)在区间[t0,t1]上 可积  定义A(t)在[t0,t1]上的积分为   1 1 0 0 () () t t ij t t A t dt a t dt m n    

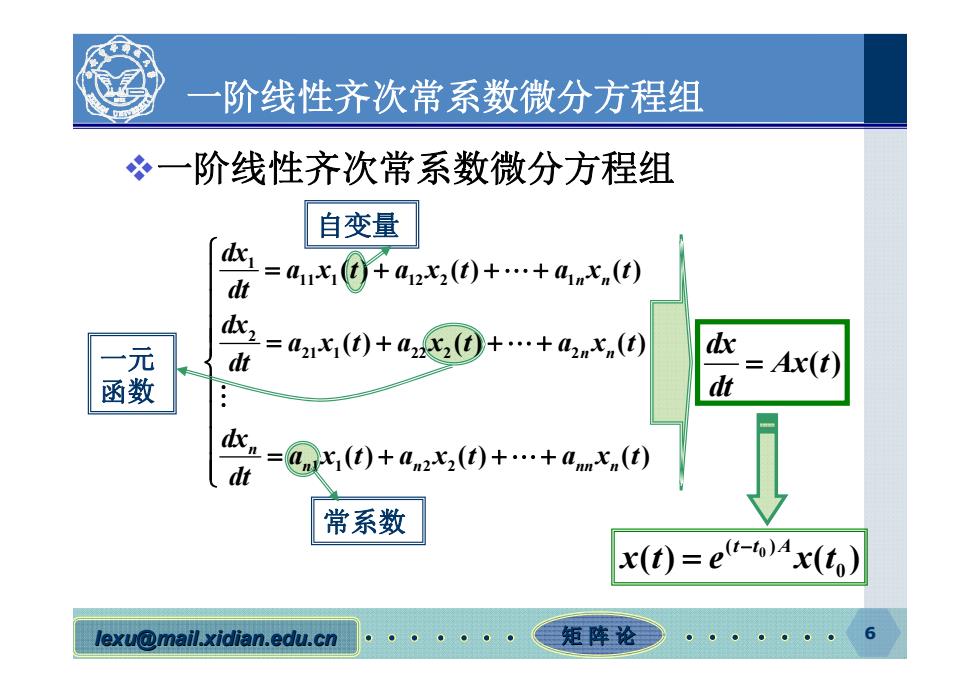
阶线性齐次常系数微分方程组 一阶线性齐次常系数微分方程组 自变量 =ax@+a,0++ar,0 dt 一元 dt =a21x(t)+a22c2(d)+…+a2nn(t) dx =Ax() 函数 dt dt =@x,()+a2x,(t)+…+anmx(t) 常系数 x(t)=e)x(t) lexu@mail.xidian.edu.cn 矩阵论●

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 一阶线性齐次常系数微分方程组 一阶线性齐次常系数微分方程组 1 11 1 12 2 1 2 21 1 22 2 2 11 22 () () () () () () () () () n n n n n n n nn n dx axt axt ax t dt dx axt axt axt dt dx axt axt axt dt                 自变量 常系数 一元 函数 ( ) dx Ax t dt  0 ( ) 0 () ( ) tt A xt e xt  

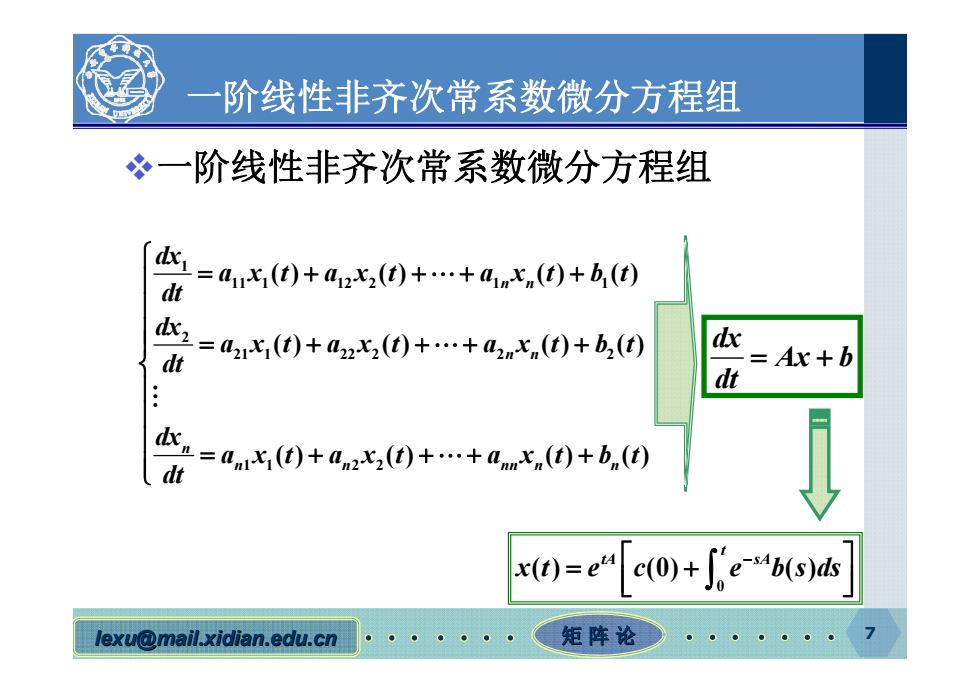
一 阶线性非齐次常系数微分方程组 一阶线性非齐次常系数微分方程组 +42-2+…+a1 =a1x0+arx0++ax,0+b,0 dt Ax+b dt =ax(国+anax,0++a,0+b,(0 dt x)=e4c0)+ie(s)dk lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 一阶线性非齐次常系数微分方程组 一阶线性非齐次常系数微分方程组 1 11 1 12 2 1 1 2 21 1 22 2 2 2 11 22 () () () () () () () () () () () () n n n n n n n nn n n dx axt axt ax t bt dt dx axt axt axt bt dt dx axt axt axt bt dt                    dx Ax b dt   0 ( ) (0) ( ) t tA sA x t e c e b s ds        

第11讲矩阵三角分解 Gauss:消元法的矩阵形式 LU分解与LDU分解 ?其他三角分解 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 第11讲 矩阵三角分解 Gauss消元法的矩阵形式 LU分解与LDU分解 其他三角分解

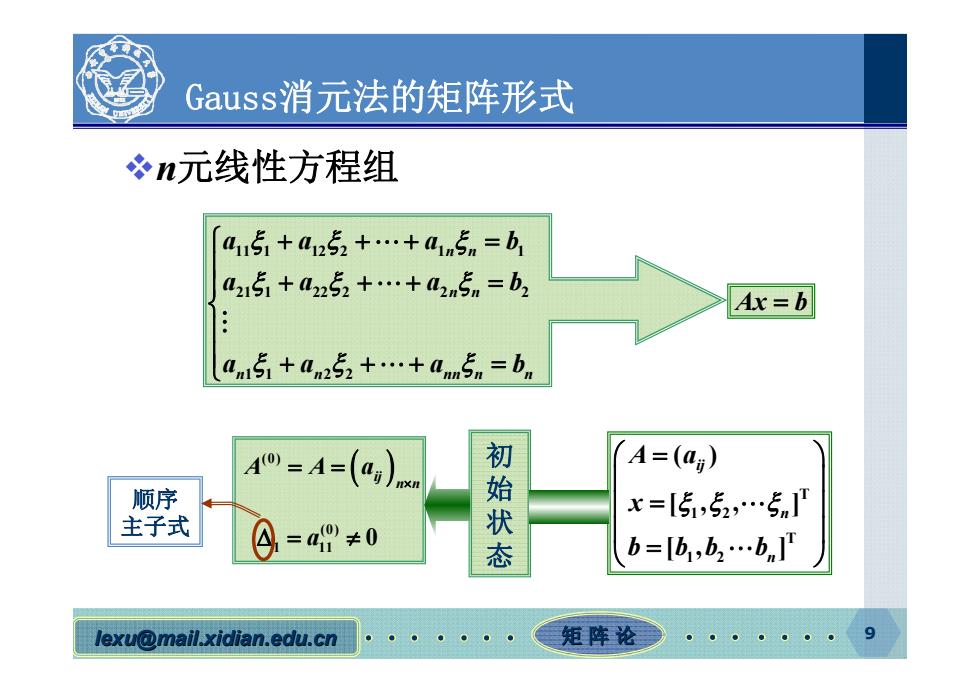
Gauss:消元法的矩阵形式 冬n元线性方程组 a51+41252+…+1n5n=b1 a215+42252+…+42n5n=b2 Ax=b n15+0n252+…+anm5n=b =(ag) 顺序 主子式 =a9≠0 初始状态 A=(ag) x=5,5,…5 b=b,b2…bn1 lexu@mail.xidian.edu.cn ● 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 Gauss消元法的矩阵形式 n元线性方程组 11 1 12 2 1 1 21 1 22 2 2 2 11 22 n n n n n n nn n n aa a b aa a b aa a b                       Ax b  T 1 2 T 1 2 ( ) [, , ] [, ] ij n n A a x b bb b                    (0) ij n n A Aa    (0) 1 11   a 0 初 始 状 态 顺序 主子式

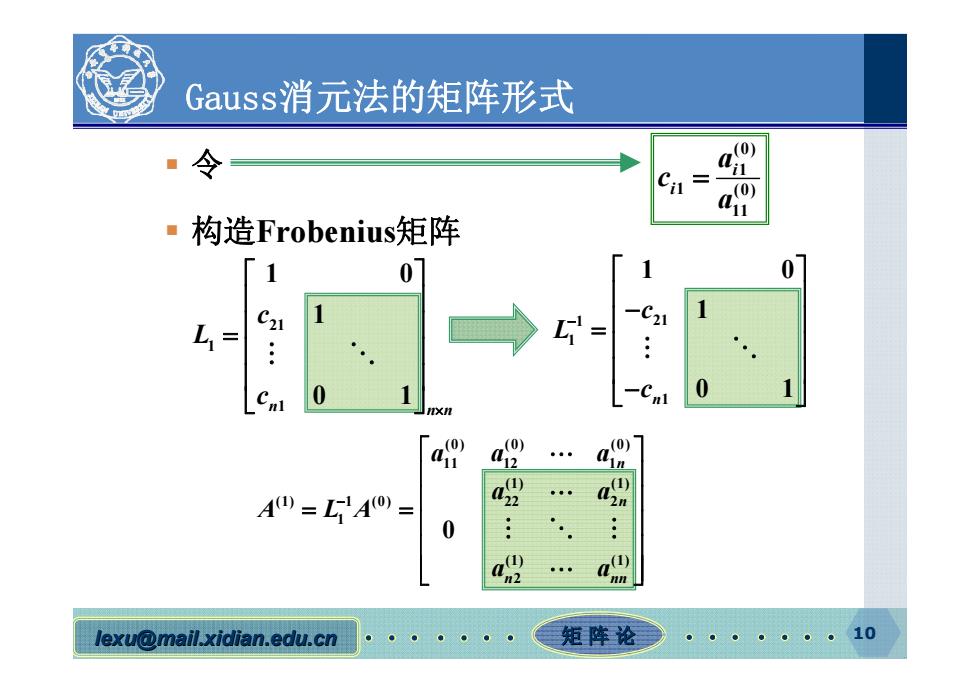
Gauss:消元法的矩阵形式 ·令 Cn= 部 ■构造Frobenius?矩阵 1 0 1 0 = C L1= 0 -Cn (0) A四=LA0= a 0 .. (1) lexu@mail.xidian.edu.cn 矩阵论 10

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 Gauss消元法的矩阵形式  令  构造Frobenius矩阵 (0) 1 1 (0) 11 i i a c a  21 1 1 1 0 1 0 1 n n n c L c                 1 21 1 1 1 0 1 0 1 n c L c                  (0) (0) (0) 11 12 1 (1) (1) (1) 1 (0) 22 2 1 (1) (1) 2 0 n n n nn aa a a a A LA a a                  