
131 矩阵论 主讲教师:徐乐 2011年11月25日星期五
lexu@mail.xidian.edu.cn

上讲回顾 第10讲矩阵的满秩分解 ·矩阵的满秩分解 ·酉对角分解与奇异值分解 lexu@mail.xidian.edu.cn 矩阵论 2
lexu@mail.xidian.edu.cn

矩阵的满秩分解 定义:设A∈Cm"(r>0) ·若存在矩阵F∈CWG∈C" ·使得A=FG ·称其为A的一个满秩分解 Note: G ·满秩分解不唯一 A= =FG 0 存在性定理 ·任何非零矩阵均存在满秩矩阵 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn
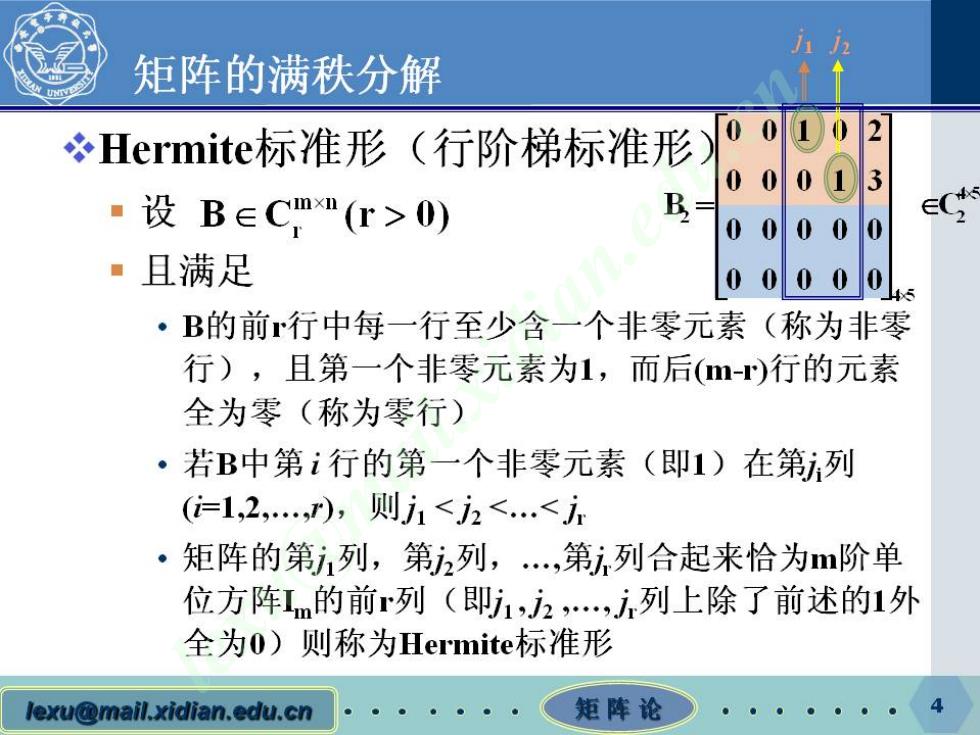
矩阵的满秩分解 冬Hermite标准形(行阶梯标准形 0 010 2 00 01 3 ·设B∈Cm"(r>0) B,= 00 00 0 ■且满足 00000 ·B的前行中每一行至少含一个非零元素(称为非零 行),且第一个非零元素为1,而后(m-)行的元素 全为零(称为零行) ·若B中第i行的第一个非零元素(即1)在第列 (=1,2…),则j1<j2<.<j ·矩阵的第j1列,第2列,,第i列合起来恰为m阶单 位方阵1m的前r列(即j1,2,,j列上除了前述的1外 全为0)则称为Hermite标准形 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn

矩阵的满秩分解 冬满秩分解的一种求法 ·设A∈CmⅫ ·行初等变换将A化成Hermite?标准形B -使得EA=B ·选取置换矩阵 -P的第i列为ej1 -其它(n一r)列只需确保P为置换矩阵即可 ·用P右乘任何矩阵 ·令G=B的前r行∈C" F=AP,∈CmT lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn
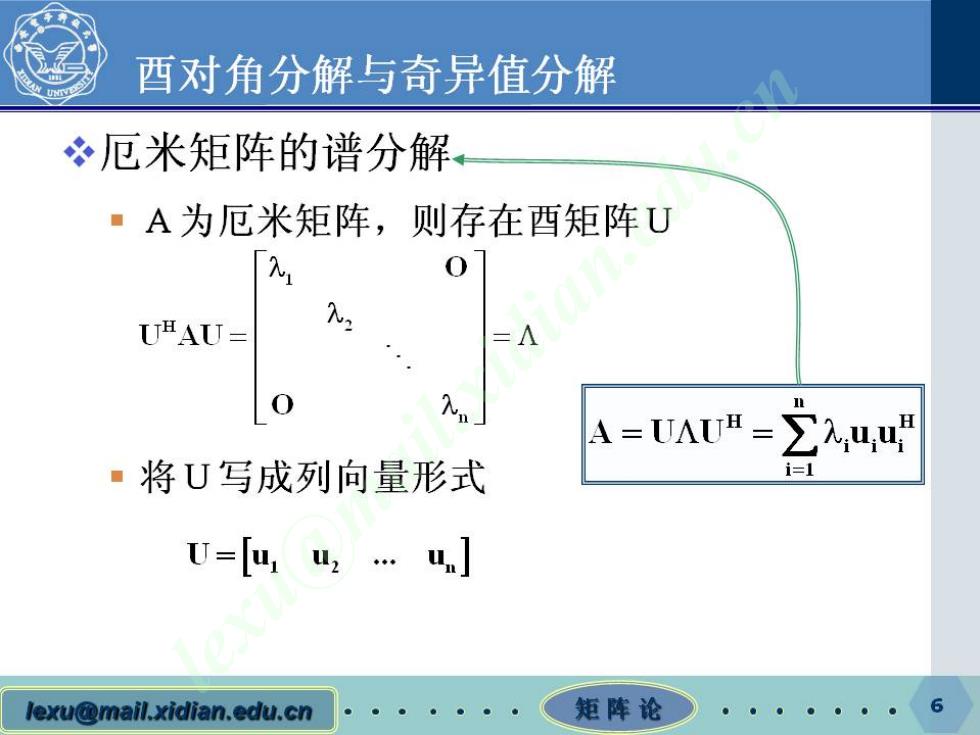
酉对角分解与奇异值分解 冬厄米矩阵的谱分解 ·A为厄米矩阵,则存在酉矩阵U 0 UBAU= 0 A=UAUH= ∑,山u ·将U写成列向量形式 i= U=[山1u,…u] lexu@mail.xidian.edu.cn 矩阵论 6
lexu@mail.xidian.edu.cn

酉对角分解与奇异值分解 冬非奇异矩阵的酉对角分解 。定理 ·设A为n阶非奇异矩阵,则存在n阶酉矩阵U及V, 使得 6 6 U"AV= o1>0(=1,2,,n) A=∑o,u i=1 ·若将U、V写成U=[u,u…u],V=[y,y:… lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn

h 酉对角分解与奇异值分解 ·酉对角分解的求法 ·先对AHA对角化(酉对角化) ·求出变换矩阵V ·再令U=AV∑ A=U∑VH lexu@mail.xidian.edu.cn 矩阵论 8
lexu@mail.xidian.edu.cn

般矩阵的奇异值分解 定理:设A∈Cmm ·则存在m阶酉矩阵U及n阶酉矩阵V,使 1 0 6 UHAV= r行 0 (m-r)行 6 0 r列 (n-r)列 6 A=U 6x lexu@mail.xidian.edu.cn 矩阵论 9
lexu@mail.xidian.edu.cn

Penrose 广义逆矩阵的定义及存在性 何谓广义 即推广了原有概念或结果 逆矩阵一般概念 ian.edu.c 针对非奇异的(或称为满秩的)方阵 这一概念可推广到 奇异方阵 非方矩阵 事实上,Penrose广义逆矩阵涵盖了两种情况 lexu@mail.xidian.edu.cn ······· 矩阵论 ······。10
lexu@mail.xidian.edu.cn