
UNIVE 矩阵论 主讲教师:徐乐 2014年12月10日星期三
2014年12月10日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 第12讲矩阵的QR分解 ·Givens矩阵与Givens7变换 "Householder2矩阵与Householderz变换 ·QR分解 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第12讲矩阵的QR分解 Givens矩阵与Givens变换 Householder矩阵与Householder变换 QR分解
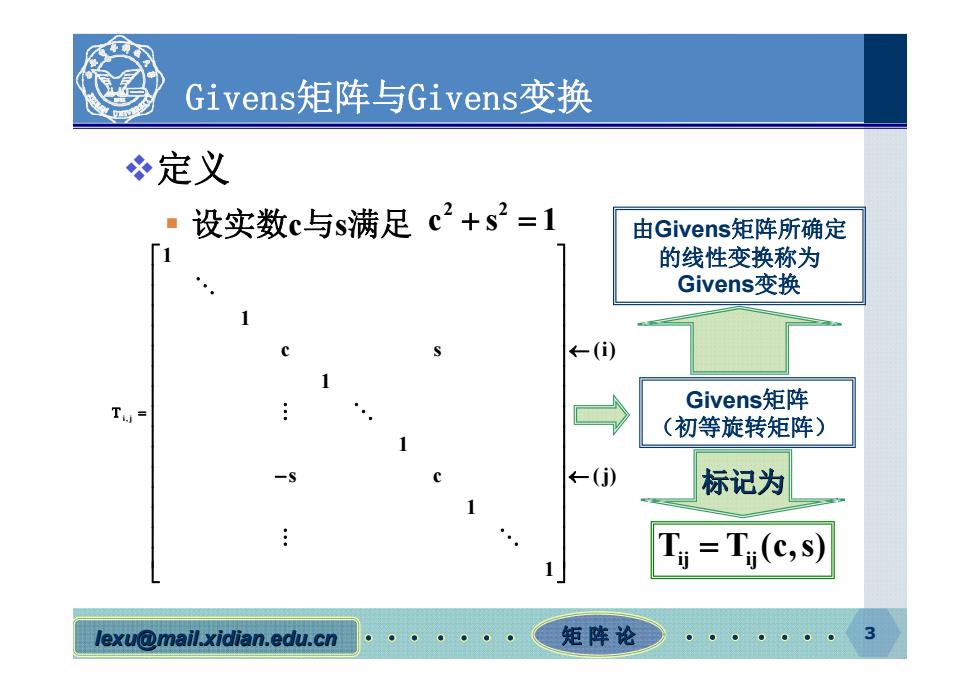
Givens矩阵与Givens?变换 冬定义 设实数c与s满足c2+s2=1 由Givens矩阵所确定 的线性变换称为 Givens变换 ←(i) Givens矩阵 T= (初等旋转矩阵) ←(j) 标记为 Ti=Tj(c,s) lexu@mail.xidian.edu.cn 矩阵论
lexu @mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 Givens矩阵与Givens变换 定义 设实数 c 与 s满足 2 2 cs1 i,j 1 1 c s (i) 1 1 s c ( j) 1 1 Givens矩阵 (初等旋转矩阵) T T (c,s) ij ij 标记为 由Givens矩阵所确定 的线性变换称为 Givens变换

Givens?矩阵与Givens?变换 性质 ·(1) [,c,]'=[T,c,s]=工,c,-) s=-sin(θ)=sin(-0) det[T,(c,)]=1 (2) K=[5,55] y=Tx=[nn2…n] 选c= 5 5 V5+号 V+另 5号+号≠0 Tx= 552…+…0… En lexu@mail.xidian.edu.cn 矩阵论●
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 Givens矩阵与Givens变换 性质 (1) (2)

Givens矩阵与Givens?变换 定理1. ·设x=[5,52…5]≠0 c1=[100…0]' ·存在有限个Givens矩阵的乘积T,使得Tx=xe, 。其中: ·x为实数时 x=V=五 ·x为复数时 x=Vx"x 冬推论 ·对于任何非零列向量x∈及任何单位列向量z=1) ·均存在着有限个Givens矩阵的乘积T ·使得Tx=z lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 Givens矩阵与Givens变换 定理1. 设 存在有限个Givens矩阵的乘积T,使得 其中: • x为实数时 • x为复数时 推论 对于任何非零列向量x∈Rn及任何单位列向量 z(|z|=1) 均存在着有限个Givens矩阵的乘积T 使得 T 12 n x 0 Tx x e 1 2 T 2 x x xx H x xx T 1 e 100 0 Tx x z

Householder?矩阵与Householder?变换 平面直角坐标系中,将向量x关于轴作镜像变换 ,则得到 y=[]0-e= 冬将其推广至n维,可定义 ·设有单位列向量u∈Rm ·则称H=L-2uur为Householderi矩阵(初等反射矩阵) ·由Householder矩阵所确定的线性变换(y=x)称为 Householder3变换 H=H(正交) T=H(实对称) H1=H(自逆) =I(对合) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 Householder矩阵与Householder变换 平面直角坐标系中,将向量x关于e1轴作镜像变换 ,则得到 将其推广至n维,可定义 设有单位列向量u∈Rn • 则称H=I-2uuT为Householder矩阵(初等反射矩阵) • 由Householder矩阵所确定的线性变换(y=Hx)称为 Householder变换 1 1 T 2 2 2 2 1 0 y I 2e e x Hx 0 1

Householder?矩阵与Householder变换 冬定理2 ·对任何非零列向量x∈R"及单位列向量z∈R” ·存在Householder矩阵H,使得H=z 选u= x-xz x-z 冬定理3 ·初等旋转矩阵(Givens矩阵)是两个初等反射 矩阵的乘积 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 Householder矩阵与Householder变换 定理2 对任何非零列向量x∈Rn及单位列向量z∈Rn 存在Householder矩阵H,使得 定理3 初等旋转矩阵(Givens矩阵)是两个初等反射 矩阵的乘积 Hx x z

QR分解 必定义 ·如果实(复)矩阵A可化为正交(酉)矩阵Q与实(复 )上三角矩阵R的乘积 ·即A=QR ·则称上式为A的QR分解 冬定理 ■设A是阶的非奇异矩阵,则存在正交(酉)矩阵Q与 实(复)上三角矩阵R ·使得A=QR ·且除去相差一个对角元素的绝对值(模)全为1的对角因子外 ,上述分解唯一 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 QR分解 定义 如果实(复)矩阵A可化为正交(酉)矩阵Q与实(复 )上三角矩阵R的乘积 • 即 • 则称上式为A的QR分解 定理 设A是n阶的非奇异矩阵,则存在正交(酉)矩阵Q与 实(复)上三角矩阵R • 使得 • 且除去相差一个对角元素的绝对值(模)全为1的对角因子外 ,上述分解唯一 A QR A QR

QR分解 冬定理5 设A是m×n的实(复)矩阵,且其n个列线性 无关,则A具有分解A=QR,其中 ·Q是m×n阶实(复)矩阵,且满足Q'Q=I(QHQ=) ·R是n阶实(复)非奇异上三角矩阵 ·除了相差一个对角元素的绝对值(模)全为1的对角 阵因子外,上述分解唯一 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 QR分解 定理5 设A是m×n的实(复)矩阵,且其n个列线性 无关,则A具有分解A=QR,其中 • Q是m×n阶实(复)矩阵,且满足 • R是n阶实(复)非奇异上三角矩阵 • 除了相差一个对角元素的绝对值(模)全为1的对角 阵因子外,上述分解唯一 T H Q Q I(Q Q I)

第13讲 QR分解及满秩分解 矩阵QR分解计算方法 矩阵的满秩分解 lexu@mail.xidian.edu.cn 矩阵论● ·。·。。。。10
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 第13讲 QR分解及满秩分解 矩阵QR分解计算方法 矩阵的满秩分解 10