
IDIAN 矩阵论 主讲教师:徐乐 2014年12月24日星期三
2014年12月24日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 第18讲广义逆的应用 ·矩阵方程AXB=D的相容性条件及通解 ·极小范数解 lexu@mail.xidian.edu.cn 矩阵论 2
lexu@mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第18讲 广义逆的应用 矩阵方程AXB=D的相容性条件及通解 极小范数解

矩阵方程AXB=D的相容性条件及通解 定理1 ■矩阵方程AXB=D相容(有解)的充要条件 AA(DDB(B=D D在相容情况下矩阵方程的通解为 {A山DB山+Y-A山AYBBY为阶数合适的任意矩阵} Note ■通解中两个A、A()及两个B、B)完全可不同 ·通解集合中,不同的Y完全可能对应同一个解 lexu@mail.xidian.edu.cn 矩阵论 3
lexu@mail.xidian.edu.cn 矩 阵 论 3 矩阵方程AXB=D的相容性条件及通解 定理1 矩阵方程AXB=D相容(有解)的充要条件 在相容情况下矩阵方程的通解为 Note 通解中两个A、A(1)及两个B、B(1)完全可不同 通解集合中,不同的Y完全可能对应同一个解 (1) (1) AA DB B D= { } (1) (1) (1) (1) A DB Y A AYBB | Y + − 为阶数合适的任意矩阵

矩阵方程AXB=D的相容性条件及通解 必推论 ·线性方程组Ax=b有解的充要条件为AA四b=b D且通解为{Ab+(L.-AA)yIy为列向量} ·A{1(AXA=A的通解)为如下集合 {AAA四+Y-AOAYAA} lexu@mail.xidian.edu.cn 矩阵论 4
lexu@mail.xidian.edu.cn 矩 阵 论 4 矩阵方程AXB=D的相容性条件及通解 推论 线性方程组Ax=b有解的充要条件为 且通解为 A{1}(AXA=A的通解)为如下集合 (1) AA b b = { } (1) (1) A b (I A A)y | y + −n 为列向量 { } (1) (1) (1) (1) A AA Y A AYAA + −

极小范数解 冬引理1 ·方程Ax=b若有解,则必存在唯一的极小范数解(对2- 范数),且该解在R(AH中 必引理2 ·A{1,4}可由如下方程的通解构成XA=AaA D其中A1,4)是A的某一个{1,4}-逆 ⑩Note:对于X∈A{L,4,XA是不变量 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 5 极小范数解 引理1 方程Ax=b若有解,则必存在唯一的极小范数解(对2- 范数),且该解在R(AH)中 引理2 A{1,4}可由如下方程的通解构成 其中A(1,4)是A的某一个{1,4}-逆 Note:对于X∈A{1,4},XA是不变量 (1,4) XA A A =

极小范数解 冬定理2 ,设A∈Cmm,则A{1,4}={Aa+Z(I-AAa,)川Z∈Cma} 冬定理3 ·设方程AX=b相容,则X=A4,b是方程的极小范数解 ·反之,若对任意b∈R(A),存在X使得Xb成为该方程的 极小范数解,则X∈A{1,4} lexu@mail.xidian.edu.cn 矩阵论 6
lexu@mail.xidian.edu.cn 矩 阵 论 6 极小范数解 定理2 定理3 设方程AX=b相容,则X=A(1,4)b是方程的极小范数解 反之,若对任意b∈R(A),存在X使得Xb成为该方程的 极小范数解,则X∈A{1,4}

第19讲最小二乘法 最小二乘法 冬极小范数最小二乘解 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 7 第19讲 最小二乘法 最小二乘法 极小范数最小二乘解
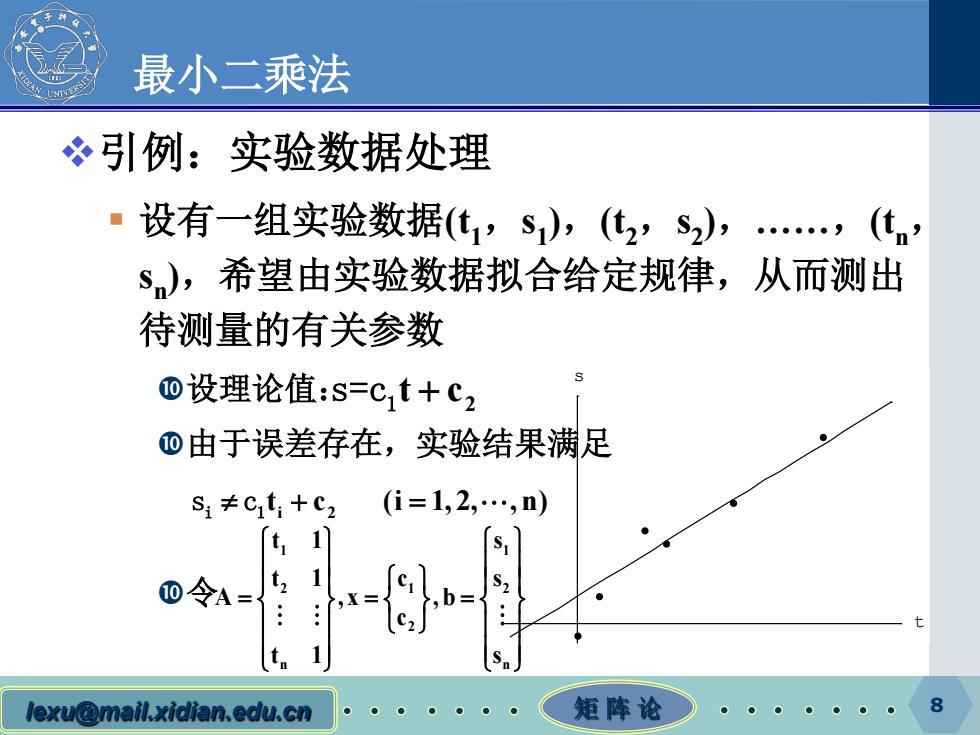
最小二乘法 冬引例:实验数据处理 设有一组实验数据(t1,S1),(2,S2),,(n, s),希望由实验数据拟合给定规律,从而测出 待测量的有关参数 ⑩设理论值:s=Ct+C2 ⑩由于误差存在,实验结果满足 s1≠Ct1+C2 (i=1,2,…,n) t 1 S1 D令A= t, 1 S2 C2 1 lexu@mail.xidian.edu.cn 矩阵论 8
lexu@mail.xidian.edu.cn 矩 阵 论 8 t s 最小二乘法 引例:实验数据处理 设有一组实验数据(t1,s1),(t2,s2),……,(tn, sn),希望由实验数据拟合给定规律,从而测出 待测量的有关参数 设理论值: 由于误差存在,实验结果满足 令 2 s=c1t c + i 2 s c i 1 ≠+ = t c (i 1, 2, , n) 1 1 2 12 2 n n t 1 s t1 c s A ,x ,b c t 1 s = = =

最小二乘法 显然,Ax=b实际无解 ·矩阵方程Ax=b成为矛盾方程(不自洽、非相容) ·但在物理上看,需要而且也理当有“解 冬一般处理是,定义一种目标函数 例如:Ec,c,)=∑w,s,-c-c,月 w,>0为加权系数 ⑩使误差最小化 w=1(i=1~n)E(c:,C2)=Ax-b lexu@mail.xidian.edu.cn 矩阵论 9
lexu@mail.xidian.edu.cn 矩 阵 论 9 最小二乘法 显然,Ax=b实际无解 矩阵方程Ax=b成为矛盾方程(不自洽、非相容) 但在物理上看,需要而且也理当有“解” 一般处理是,定义一种目标函数 例如: 使误差最小化 wi =1(i=1~n)时 ? n 2 1 2 i i 1i 2 i i 1 E(c ,c ) w (s c t c ) w 0 = = −− > ∑ 为加权系数 2 1 2 2 E(c ,c ) Ax b = −

最小二乘法(解) 对于矛盾方程Ax=b,最小二乘法是求其 “解”的一种方法 ·即Ax-b2=min 冬引理 ·设A∈Cm×n,A{1,3}由如下方程的通解构成: AX=AA(1.3)Af1,3)={A(1.3)+(I-A(13)A)ZZECnxm) 0其中,A(1,3)为A{1,3}中的某个矩阵 lexu@mail.xidian.edu.cn 矩阵论 10
lexu@mail.xidian.edu.cn 矩 阵 论 10 最小二乘法(解) 对于矛盾方程Ax=b,最小二乘法是求其 “解”的一种方法 即 引理 设A∈Cm×n ,A{1,3}由如下方程的通解构成: 其中,A(1,3)为A{1,3}中的某个矩阵 2 Ax b min − = (1,3) (1,3) (1,3) n m AX AA A{1, 3} {A (I A A)Z Z C } × = → = +− ∈