西安电子科技大学：《矩阵论》研究生课程教学课件（讲义，2015）23 广义特征值与极小极大原理

矩阵论 主讲教师：徐乐 2015年1月13日星期二

2015年1月13日星期二 矩 阵 论 主讲教师：徐乐

上讲回顾 ÷第22讲矩阵特征值估计 ·特征值界的估计 ·盖尔圆法 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第22讲 矩阵特征值估计  特征值界的估计  盖尔圆法

特征值界的估计 冬矩阵特征值估计 ·特征值计算较困难，希望找到简便的特征值界 限或分布范围的估计方法 冬定理1 ·设A∈R×n,为A的任意特征值，则有 m()sx-D ·其中 M=max ai-ai 1Si,jSn 2 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 特征值界的估计 矩阵特征值估计  特征值计算较困难，希望找到简便的特征值界 限或分布范围的估计方法 定理1  设A∈Rn×n，λ为A的任意特征值，则有 • 其中   nn 1   Im M 2   ij ji 1 i,j n a a M max   2  

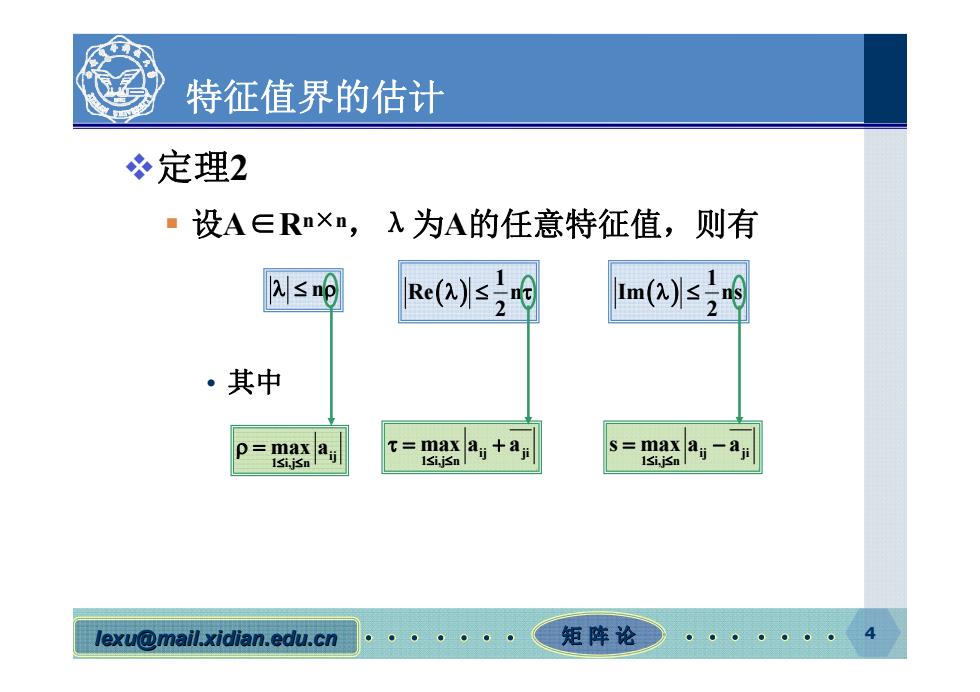
特征值界的估计 冬定理2 ·设A∈Rn×n,入为A的任意特征值，则有 ≤吗 Re()s Im(Z)s ·其中 p=maxa可 t=max ai +a s=max ai-aj 1si,jSn 1Si,jSn l 1si,iSn I lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 特征值界的估计 定理2  设A∈Rn×n，λ为A的任意特征值，则有 • 其中  n   1 Re n2      1 Im ns 2   ij 1 i,j n max a     ij ji 1 i,j n max a a     ij ji 1 i,j n s max a a    

盖尔圆法 必定义 ·设A=(anXn∈RnXn, 由方程所确定的圆称为A 的第个盖尔圆，R称为盖尔圆的半径 -R,=aol izi 定理3 ·矩阵A的所有特征值均落在它的所有盖尔圆的 并集之中 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 盖尔圆法 定义  设A=(ai,j)n×n∈Rn×n，由方程所确定的圆称为A 的第i个盖尔圆，Ri称为盖尔圆的半径 定理3  矩阵A的所有特征值均落在它的所有盖尔圆的 并集之中 n ii i ij j 1 i j za R a    

盖尔圆法 冬定理4 ·将矩阵A的全体盖尔圆的并集按连通部分分成 若干个子集 ·一个子集由完全连通的盖尔圆组成，不同子集没有 相连通的部分 ·对每个子集，若它恰好由K个盖尔圆组成，则该子 集中恰好包含A的K个特征值 ·说明 ·盖尔圆相互重叠时重复计算，特征值相重时也重复 计算 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 盖尔圆法 定理4  将矩阵A的全体盖尔圆的并集按连通部分分成 若干个子集 • 一个子集由完全连通的盖尔圆组成，不同子集没有 相连通的部分 • 对每个子集，若它恰好由K个盖尔圆组成，则该子 集中恰好包含A的K个特征值  说明 • 盖尔圆相互重叠时重复计算，特征值相重时也重复 计算

盖尔圆法 冬推论 ·孤立盖尔圆中恰好包含一个特征值 实矩阵的孤立盖尔圆恰好包含一个实特征值 ·盖尔圆方法中盖尔圆半径可以按列求和（因为方 阵转置后特征值不变) ·盖尔圆半径变为R,两个盖尔圆定理仍然成立 a i=1 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 盖尔圆法 推论  孤立盖尔圆中恰好包含一个特征值  实矩阵的孤立盖尔圆恰好包含一个实特征值  盖尔圆方法中盖尔圆半径可以按列求和(因为方 阵转置后特征值不变)  盖尔圆半径变为Ri，两个盖尔圆定理仍然成立 n ' i i ij j 1 j R a     

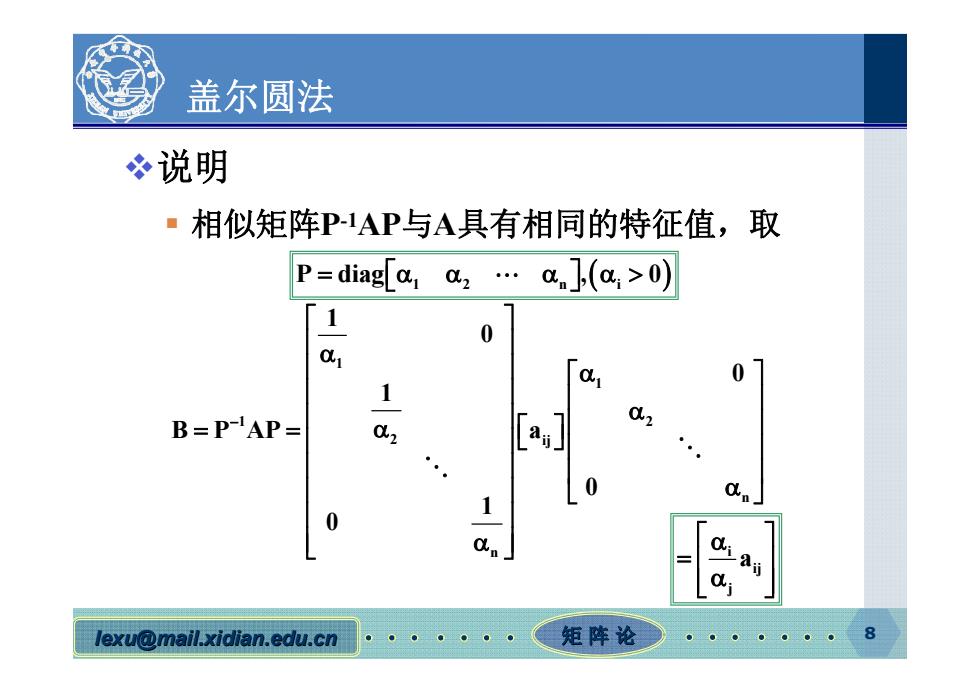
盖尔圆法 说明 ·相似矩阵P1AP与A具有相同的特征值，取 P=diag[a az.a(a>0) 1 0 01 0 1 B=PAP= &2 02 0 0 lexu@mail.xidian.edu.cn 矩阵论→

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 盖尔圆法 说明  相似矩阵P-1AP与A具有相同的特征值，取 P diag , 0        12 n i      1 1 1 2 2 ij n n 1 0 0 1 B P AP a 0 1 0                                             i ij j a       

第23讲广义特征值与极小极大原理 冬广义特征值问题 瑞利商 冬极小极大原理 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 第23讲 广义特征值与极小极大原理  广义特征值问题  瑞利商  极小极大原理

广义特征值问题 冬定义 ·设A、B为n阶方阵，若存在数入，使得方程 Ax=λBx存在非零解 ·则称入为A相对于B的广义特征值 ·x为A相对于B的属于广义特征值入的特征向量 一是标准特征值问题的推广 ©当B=I（单位矩阵)时，广义特征值问题退化为标准 特征值问题。 一特征向量是非零的 lexu@mail.xidian.edu.cn 矩阵论 10

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 广义特征值问题 定义  设A、B为n阶方阵，若存在数λ，使得方程 Ax=λBx存在非零解 • 则称λ为A相对于B的广义特征值 • x为A相对于B的属于广义特征值λ的特征向量 – 是标准特征值问题的推广 当B＝I（单位矩阵）时，广义特征值问题退化为标准 特征值问题。 – 特征向量是非零的