
场论与复变函数 主讲:徐乐
场论与复变函数 主讲:徐乐

Review 孤立奇点 若f(a)在z解析,z,为函数f的m级墨点的充要条件: 。fm(a)=0,(=0,1,2,,m-l) ·fm(z)0 奇点类型 洛朗级数 lim f(z) 零点极点 2-→20 可去奇点 A)-c.- 存在且 n=0 有限:co f(z=(2-2o)"mg(2) M级极点 A()-c-a 00 若z为函数1/f(e)的m级零点, 则zo为函数f(z)的m级极点 本性奇点 f)-c- 不存在且 不为0 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 矩阵论 2 Review 孤立奇点 若f (z)在z0解析,z0为函数f (z)的m级零点的充要条件: f (n)(z0) = 0,(n=0,1,2,…,m-1) f (m)(z0) ≠0 奇点类型 洛朗级数 零点极点 可去奇点 M级极点 本性奇点 0 lim ( ) z z f z 0 0 () ( )n n n f z cz z 0 -m () ( )n n n fz c z z 0 - () ( )n n n fz c z z 存在且 有限:c0 ∞ 不存在且 不为∞ f (z)=(z-z0)-mg(z) 若z0为函数1/f (z)的m级零点, 则z0为函数f (z)的m级极点

Review ·若函数fz)在无穷远点x=oo的去心领域R<z<+oo内 解析,则称点o为fz)的孤立奇点 ■作变换t=1z ·将去心领域R<zk+oo内对函数fz的研究化为在去心领域 0<k1/R内对函数p()的研究 ·显然()在去心领域0<<1/R解析,仁0为函数(⑩的孤立奇点 ·若t=0是p()的可去奇点、m级极点或本性奇点,则称 点z=oo是fz)的可去奇点、m级极点或本性奇点 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 3 Review 若函数f(z)在无穷远点 z=∞的去心领域R<|z|<+ ∞内 解析,则称点∞为f(z)的孤立奇点 作变换 t = 1/z • 将去心领域R<|z|<+ ∞内对函数f(z)的研究化为在去心领域 0<|t|<1/R内对函数φ(t)的研究 • 显然φ(t)在去心领域0<|t|<1/R解析,t=0为函数φ(t)的孤立奇点 若 t =0是φ(t)的可去奇点、m级极点或本性奇点,则称 点z=∞是f(z)的可去奇点、m级极点或本性奇点
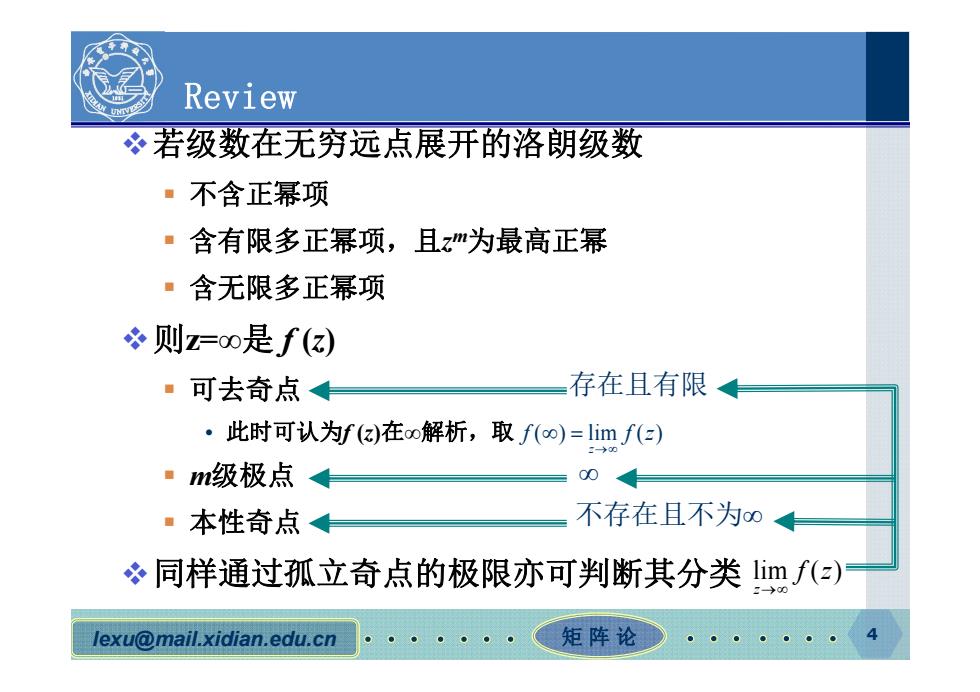
Review 若级数在无穷远点展开的洛朗级数 ·不含正幂项 ·含有限多正幂项,且zm为最高正幂 ·含无限多正幂项 则z=o是f() ·可去奇点《 存在且有限 ·此时可认为f)在oo解析,取f(o)=limf(a) m级极点 004 ·本性奇点 不存在且不为0 同样通过孤立奇点的极限亦可判断其分类limf(z) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 4 Review 若级数在无穷远点展开的洛朗级数 不含正幂项 含有限多正幂项,且zm为最高正幂 含无限多正幂项 则z=∞是 f (z) 可去奇点 • 此时可认为f (z)在∞解析,取 m级极点 本性奇点 同样通过孤立奇点的极限亦可判断其分类 lim ( ) z f z 存在且有限 ∞ 不存在且不为∞ ( ) lim ( ) z f f z

第20讲留数 留数及留数定理 留数计算 在无穷远点的留数 留数在定积分中的应用(① lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 5 第20讲 留数 留数及留数定理 留数计算 在无穷远点的留数 留数在定积分中的应用(I)

留数及留数定理 冬回顾柯西-古萨基本定理 ∮f5d5-9 函数在区域D内解析,C为区域D内任意一条简单闭曲 线,则∮f(5)d5=0 冬回顾洛朗级数的在积分中的应用 ·若z为函数在区域D内的一个奇点,C为z,去心邻域内 任意一条简单闭曲线,则∮。f5)d5=2πic ·若函数在区域D内除在点z,乙1,,zn外的处处解析 ,C为z去心邻域内任意一条简单闭曲线,则 ∮f5)d5=? lexu@mail.xidian.edu.cn ● 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 6 留数及留数定理 回顾柯西-古萨基本定理 函数在区域D内解析,C为区域D内任意一条简单闭曲 线,则 回顾洛朗级数的在积分中的应用 若z0为函数在区域D内的一个奇点, C为z0去心邻域内 任意一条简单闭曲线,则 若函数在区域D内除在点z0, z1 ,…, zn外的处处解析 , C为z0去心邻域内任意一条简单闭曲线,则 () 0 C f d 1 () 2 C f d ic () ? C f d () ? C f d

留数及留数定理 2πi,n=0 留数定义: em 10 ,n≠0 ·若为函数fz)的一个孤立奇点 ·C为z的某个去心邻域0<z-zoKR内包含z的任意一条 正向简单闭曲线 ·将函数在该去心邻域内展开成洛朗级数 f(z)=…+cn(2-2o)"+…+c1(2-2o)+c+c(2-20)+…+cn(2-2o)”+… ·对上式两端同时沿C作积分,则 Φf5)d5=2πic. ·该留下的积分值除以2πi后得到的数称为f(z)在z的留数 ,记作Reslf(),l ·显然有 Rea以,l=2∮.fe lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 7 留数及留数定理 留数定义: 若z0为函数 f (z) 的一个孤立奇点 C为z0的某个去心邻域 0<|z- z0 |<R 内包含z0的任意一条 正向简单闭曲线 将函数在该去心邻域内展开成洛朗级数 • 对上式两端同时沿C作积分,则 该留下的积分值除以2πi后得到的数称为f (z)在z0的留数 ,记作 Res[f (z),z0] 显然有 f (z) cn (z z0 )n c1(z z0 )1 c0 c1(z z0 ) cn (z z0 )n 1 0 1 ( )n C dz z z 2, 0 0 , 0 i nn 1 () 2 C f d ic 0 1 1 Re [ ( ), ] ( ) 2 C s f z z f z dz c i

留数及留数定理 冬留数定理 ·设函数f(z)在区域D内除有限个孤立奇点z0,乙1,… ,乙m外处处解析,C为D内包围诸奇点的一条正向简单 闭曲线,则 9f(e)dk=2πi∑ResIf(=),] k= 22 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 8 留数及留数定理 留数定理 设函数 f (z)在区域D内除有限个孤立奇点z0 , z1, … , zn外处处解析, C为D内包围诸奇点的一条正向简单 闭曲线,则 1 ( ) 2 Re [ ( ), ] n k C k f z dz i s f z z z2 z1 zk zn z3 D

留数及留数定理 ·[证明]欲求积分∮f(z)d正 ·把C内的所有奇点乙0,乙1,…,乙n用互不包含的正 向简单闭曲线C包围起来 ·由复合闭路定理可知 ∮fet-∮fet ·由留数的定义可知④。f(z)d止=2πic1=2πiRes[f(e),z】 ·因此可得∮fe)t=2πi∑Reslf(z)),] ·即证 lexu@mail.xidian.edu.cn 矩阵论●
lexu@mail.xidian.edu.cn 矩阵论 9 留数及留数定理 [证明]欲求积分 • 把C内的所有奇点z0 , z1, … , zn用互不包含的正 向简单闭曲线Ck包围起来 • 由复合闭路定理可知 • 由留数的定义可知 • 因此可得 • 即证 ( ) C f z dz 1 () () k n C C k f z dz f z dz 1 ( ) 2 2 Re [ ( ), ] k k C f z dz ic i s f z z 1 ( ) 2 Re [ ( ), ] n k C k f z dz i s f z z

留数及留数定理 Note1:留数定理将封闭曲线C的积分转化成fz) 在C中各孤立奇点处的留数计算 Note2:如何有效求出f(z)在孤立奇点处的留数 ? ·可去奇点:留数为零 ·本性奇点:把函数展开成为洛朗级数求得c1,即留数 ·极点:根据极点的性质采用不同的规则侧简化留数计算 lexu@mail.xidian.edu.cn 矩阵论 10
lexu@mail.xidian.edu.cn 矩阵论 10 留数及留数定理 Note1:留数定理将封闭曲线C的积分转化成 f(z) 在C中各孤立奇点处的留数计算 Note2:如何有效求出 f (z) 在孤立奇点处的留数 ? 可去奇点:留数为零 本性奇点:把函数展开成为洛朗级数求得c-1,即留数 极点:根据极点的性质采用不同的规则简化留数计算