西安电子科技大学：《复变函数与场论》课程教学课件（讲义，2016）第18讲 幂级数及泰勒级数

场论与复变函数 主讲：徐乐

场论与复变函数 主讲：徐乐

Review ”复数项级数 ·复数列的极限 {an收敛e {an收敛 {b,收敛 ·复级数 lim a=a 三4收敛 1-y0 2a,收敛 收敛园 冬幂级数 {Sn ■幂级数 三收敛 ■收敛园与收敛半径 lexu@mail.xidian.edu.cn 复变函数●)。。。。。。。 2

lexu@mail.xidian.edu.cn 复变函数 Review v复数项级数 § 复数列的极限 § 复级数 v幂级数 § 幂级数 § 收敛园与收敛半径     n n lim 1 n n     {sn} 1 1 1 n n n n n n a b            收敛 收敛 收敛 { } { } { } n n n a b   收敛 收敛 收敛 收敛园 0 n n n c z    2

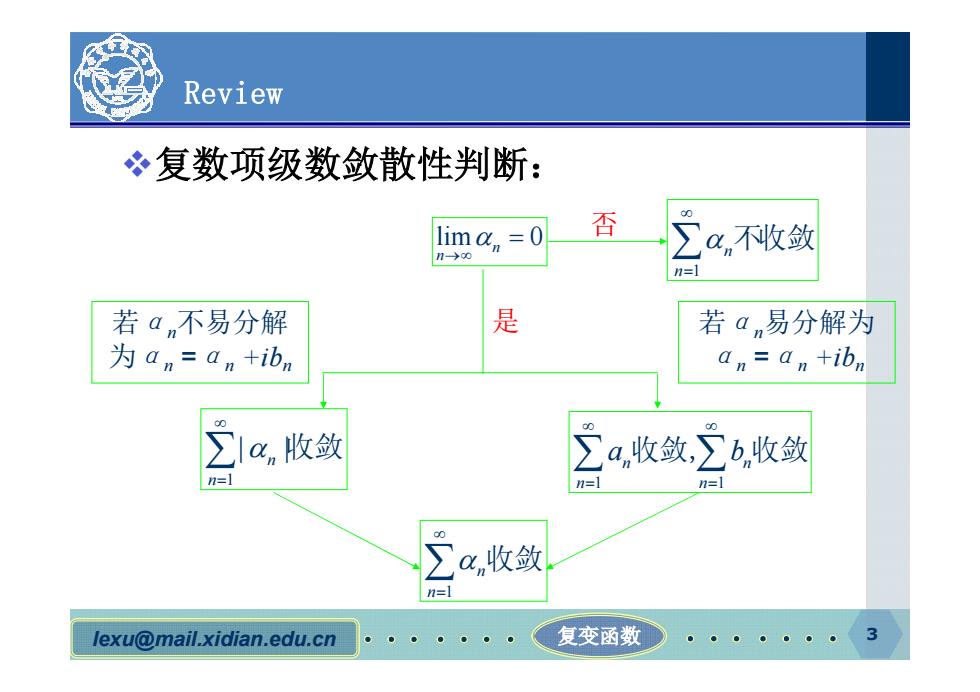
Review 复数项级数敛散性判断： lima =0 否 1→00 ∑a,不收敛 n= 若an不易分解 是 若an易分解为 为an=am+ibm an=an +ibn ∑la,收敛 ∑a,收敛∑b收敛 n=1 ∑a,收敛 n=1 lexu@mail.xidian.edu.cn 复变函数

lexu@mail.xidian.edu.cn 复变函数 Review v复数项级数敛散性判断： lim 0 n n    否 1 1 n n n n a b       收敛, 收敛 1 | | n n     收敛 若α n不易分解 为α n =α n +ibn 若α n易分解为 α n =α n +ibn 是 1 n n     收敛 1 n n     不收敛 3

第17讲幂级数及泰勒级数 幂级数 ·收敛半径的求法 ·幂级数的运算和性质 冬泰勒级数 lexu@mail.xidian.edu.cn 复变函数 4

lexu@mail.xidian.edu.cn 复变函数 第17讲 幂级数及泰勒级数 v幂级数 § 收敛半径的求法 § 幂级数的运算和性质 v泰勒级数 4

幂级数 ·幂级数收敛半径的求法 ·比值法 ⑩若 lim 元≠0 R= 1→0 ■根植法 Cn ⑩若 limc|=u≠0 R=1 ·Note1:”若(4，)=0，则R=o, 即级数在复平 面内处处收敛 ■Note2: 若(4，九)）=00，」 则R=0,即级数在除原 点外的复平面处处发散 lexu@mail.xidian.edu.cn 复变函数●

lexu@mail.xidian.edu.cn 复变函数 幂级数 v幂级数收敛半径的求法 § 比值法 •若 § 根植法 •若 § Note1：若(μ,λ)=0，则R=∞，即级数在复平 面内处处收敛 § Note2：若(μ,λ)=∞ ，则R=0，即级数在除原 点外的复平面处处发散 1 lim 0 n n n c c      1 R   lim | | 0 n n n c     1 R   5

幂级数 。比值法证明： ·[证考察级数∑1c,”1 由正项级数审敛法则可知，当 =lim ==p1 D即∑1c川”1发散，与已知矛盾， 因此当心1/x时级数发散 lexu@mail.xidian.edu.cn ● 复变函数 6

lexu@mail.xidian.edu.cn 复变函数 幂级数 v比值法证明： § [证]考察级数 § 由正项级数审敛法则可知，当 •级数收敛 •即|z|1/ λ时，级数发散 •反证。假设在|z|=1/ λ外有一点z0使级数收敛，在圆外另取一 点z1，使得|z1| 1/ λ，所以 •即 发散，与已知矛盾，因此当|z|>1/ λ时级数发散 0 | | n n n c z    1 1 1 | | lim lim 1 | | n n n n n n n n c z c z z c z c            1 0 | || | n n n c z   1  1 1 1 1 | | lim 1 | | n n n n n c z z c z         1 0 | || | n n n c z    级数的 收敛半径为 1 R   6

幂级数 冬根值法证明： ·[证]考察级数c ·由正项级数审敛法则可知，当 limc,="|=limc,==po0 ⑩级数收敛一 收敛半径为 D即☑l 即∑c‖”|发散，与已知矛盾，因此当z小1/入时级数发散 lexu@mail.xidian.edu.cn ●0● 复变函数

lexu@mail.xidian.edu.cn 复变函数 幂级数 v根值法证明： § [证]考察级数 § 由正项级数审敛法则可知，当 •级数收敛 •即|z|1/ λ时，级数发散 •反证。假设在|z|=1/ λ外有一点z0使级数收敛，在圆外另取一 点z1，使得|z1| 1/ λ，所以 •即 发散，与已知矛盾，因此当|z|>1/ λ时级数发散 0 | | n n n c z    lim | | lim | | 1 n n n n n n n c z c z z         1 0 | || | n n n c z    1 1 1 lim | | lim | | 1 n n n n n n n c z c z z         1 0 | || | n n n c z    级数的 收敛半径为 1 R   7

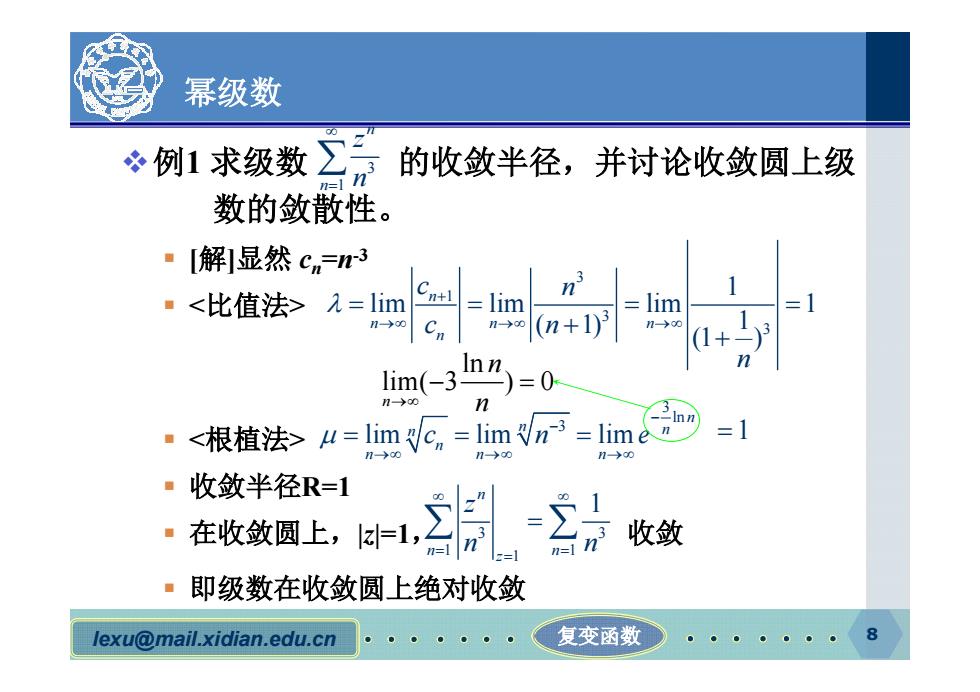
幂级数 例1求级数 的收敛半径，并讨论收敛圆上级 数的敛散性。 ·[解]显然cn=3 ·=lim =lim lim n-→0 n-→(n+1)3 n→0 (1+-) Inn lim(-3)=0 7>o0 n 3 。u=limc=lim√n3=lime =1 1→c0 ■收敛半径R=1 ·在收敛圆上，上 收敛 11 ·即级数在收敛圆上绝对收敛 lexu@mail.xidian.edu.cn 复变函数 8

lexu@mail.xidian.edu.cn 复变函数 幂级数 v例1 求级数 的收敛半径，并讨论收敛圆上级 数的敛散性。 § [解]显然 cn=n-3 § § § 收敛半径R=1 § 在收敛圆上，|z|=1， 收敛 § 即级数在收敛圆上绝对收敛 3 1 n n z n    3 1 3 3 1 lim lim lim 1 ( 1) 1 (1 ) n n n n n c n c n n            3 ln 3 lim lim lim n n n n n n n n  c n e        ln lim( 3 ) 0 n n  n    1 3 3 1 1 1 1 n n n z z n n        8

幂级数的运算和性质 复变幂级数的运算 ·代数运算性质： D设有两个幂级数，其特性如下 fa)=∑a,2”,R=r n=0 R=min(,) g(e)=∑b,2”,R=5 g则幂级数在z<R的圆内进行代数运算所得幂级 数的和函数分别是fz)、(z)的代数运算结果 fe)±ge)=∑a,"±∑，”=∑(a,±6，) =0 lexu@mail.xidian.e e)ge)=∑a,6,-2b

lexu@mail.xidian.edu.cn 复变函数 幂级数的运算和性质 v复变幂级数的运算 § 代数运算性质： •设有两个幂级数，其特性如下 –则幂级数在|z|<R的圆内进行代数运算所得幂级 数的和函数分别是f(z)、g(z)的代数运算结果 1 0 2 0 ( ) , ( ) , n n n n n n f z a z R r g z b z R r           R r r  min( , ) 1 2 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ) ( ) n n n n n n n n n n n n n n n k n k n n n k f z g z a z b z a b z f z g z a z b z a b z                                9

幂级数的运算和性质 Note::两幂级数经过代数运算得到的新幂级数收敛 半径为R,但它们只能在<R内有以上的代数 运算性质 ·复合运算性质： ®若当1Kr时，fG)=∑a,s n=0 o当lz<R时，g(z解析且满足g(z<r,则当z<R时 fg(-)-a.Ix( lexu@mail.xidian.edu.cn 复变函数 10

lexu@mail.xidian.edu.cn 复变函数 幂级数的运算和性质 •Note：两幂级数经过代数运算得到的新幂级数收敛 半径为R，但它们只能在|z|<R内有以上的代数 运算性质 § 复合运算性质： •若当|ζ|<r时， •当|z|<R时，g(z)解析且满足|g(z)|<r，则当|z|<R时 0 ( ) n n n f a       0 [ ( )] [ ( )]n n n f g z a g z     10