
1931 场论与复变函数 场论篇 主讲:徐乐
场论与复变函数 场论篇 主讲:徐乐
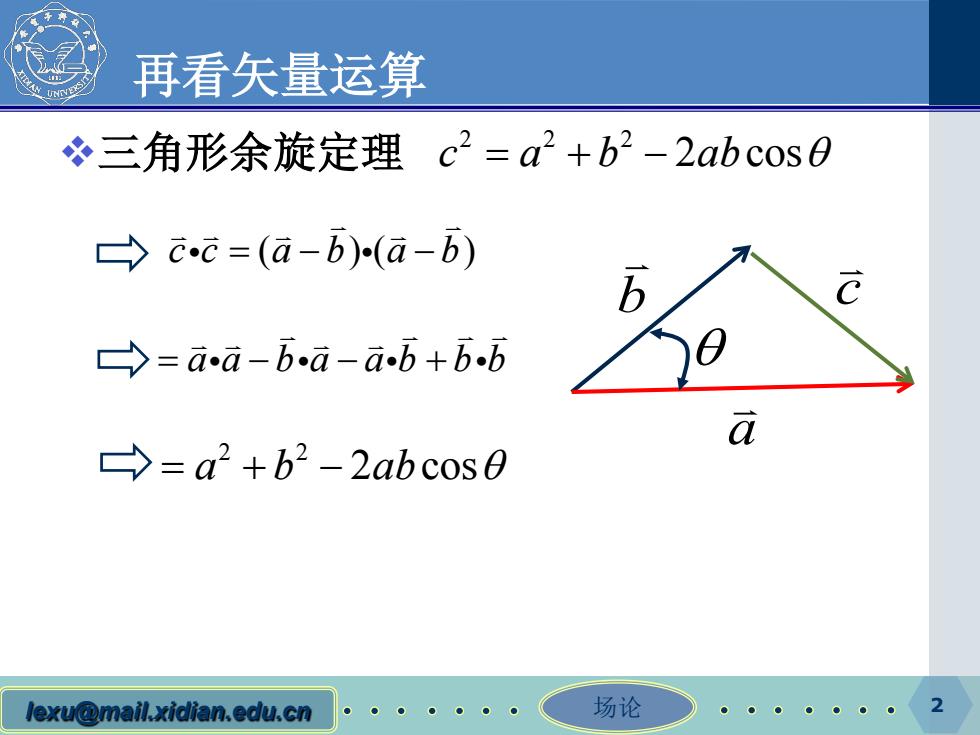
再看矢量运算 三角形余旋定理c2=a2+b2-2 ab cos.0 cc=(a-b)-(a-b) C =aa-b-a-a-b+b.b a →=a2+b2-2 ab cos0 lexu@mail.xidian.edu.cn 场论 2
lexu@mail.xidian.edu.cn 场论 再看矢量运算 三角形余旋定理 2 a b c θ 2 22 c a b ab =+− 2 cosθ cc a b a b =− − ( )( ) =−−+ aa ba ab bb 2 2 =+− a b ab 2 cosθ
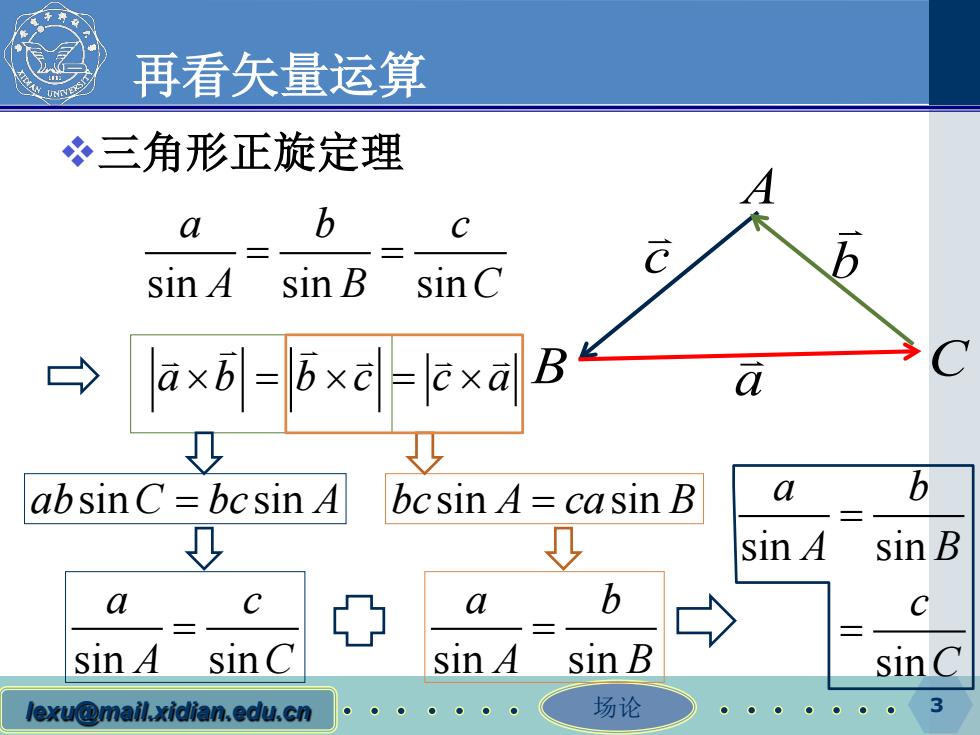
再看矢量运算 冬三角形正旋定理 a b C sin 4 sin B sin C axB-Bxcl-kxal B a absinC=bcsin A bcsin A=casin B a b ↓ sin 4 sin B a C a b C sin 4 sinC sin 4 sin B sinC lexu@mail.xidian.edu.cn ●●● 场论 3
lexu@mail.xidian.edu.cn 场论 再看矢量运算 三角形正旋定理 3 a b c sin sin sin abc ABC = = ab bc ca ×=×=× A B C ab C bc A sin sin = sin sin a c A C = bc A ca B sin sin = sin sin a b A B = sin sin sin a b A B c C = =
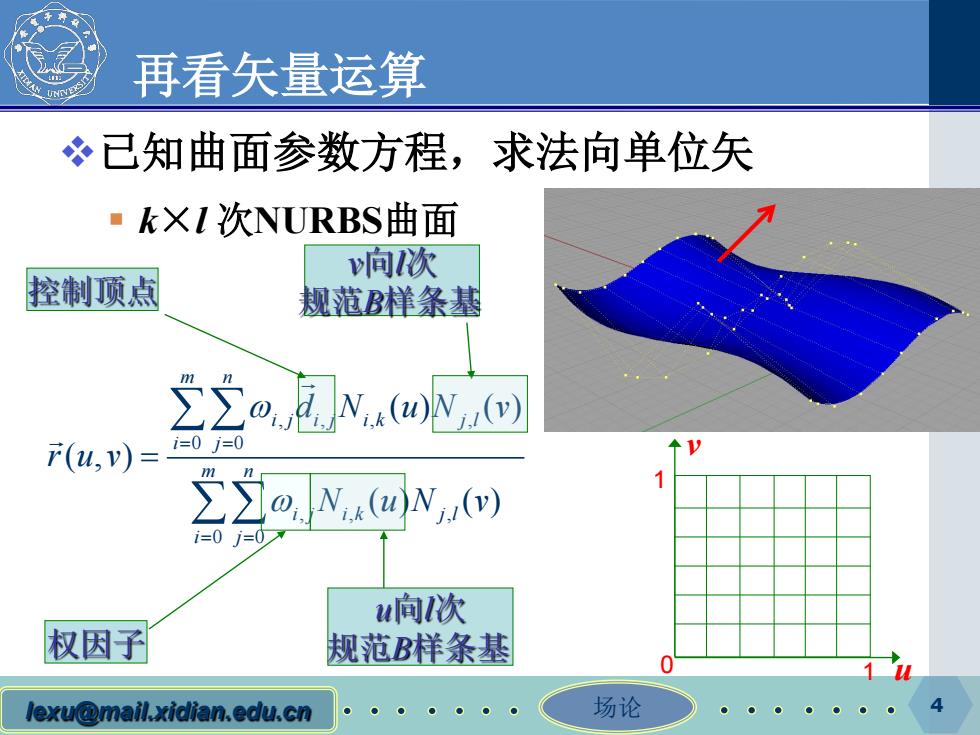
再看矢量运算 冬已知曲面参数方程,求法向单位矢 ·kXI次NURBS曲面 间次 控制项点 规范B样条基 r(u,v)= 空b ∑oN@N,) =0i=0 w间次 权因子 规范B样条基 0 lexu@mail.xidian.edu.cn ●●●●● 场论 ● 4
lexu@mail.xidian.edu.cn 场论 再看矢量运算 已知曲面参数方程,求法向单位矢 k×l 次NURBS曲面 4 ruv (,) = u v 1 1 0 ,, , , 0 0 ,, , 0 0 () () (,) () () m n i j i j ik jl i j m n i j ik jl i j d N uN v ruv N uN v ω ω = = = = = ∑∑ ∑∑ 权因子 控制顶点 v向l次 规范B样条基 u向l次 规范B样条基

再看矢量运算 冬导矢的应用 (u,)三 P(u,v) 网四 @(u,v) 元(u,y)=卫,-@(u,ru,) @(u,v) n=ruxrv F(u,)=D,(,)-@,4,)F(u,) n= n @(u,v) lexu@mail.xidian.edu.cn 场论
lexu@mail.xidian.edu.cn 场论 再看矢量运算 导矢的应用 5 (,) (,)(,) (,) (,) u u u p uv uvruv r uv u v ω ω − = (,) (,)(,) (,) (,) v v v p uv uvruv r uv u v ω ω − = ˆ | | nr r u v n n n = × = ,, , , ,, , () () (,) (,) (,) () () Ik Jl i j i j jl ik iI jJ Ik Jl i j jl ik iI jJ dN v N u puv ruv u v N vN u ω ω ω + + = = + + = = = = ∑ ∑ ∑ ∑
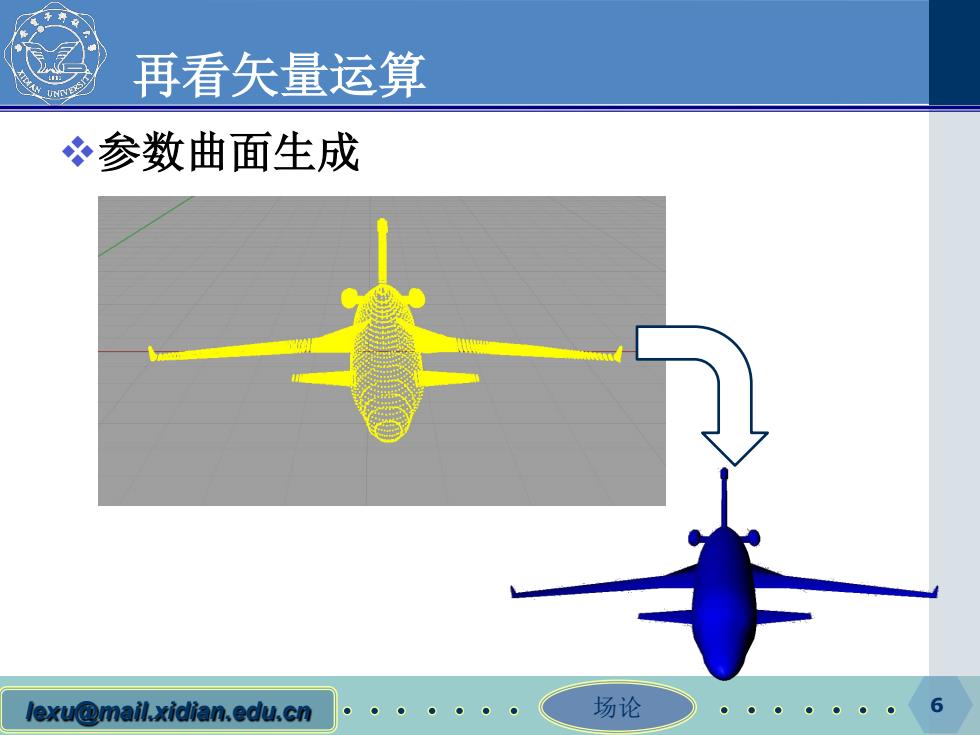
再看矢量运算 冬参数曲面生成 lexu@mail.xidian.edu.cn 场论 6
lexu@mail.xidian.edu.cn 场论 再看矢量运算 参数曲面生成 6
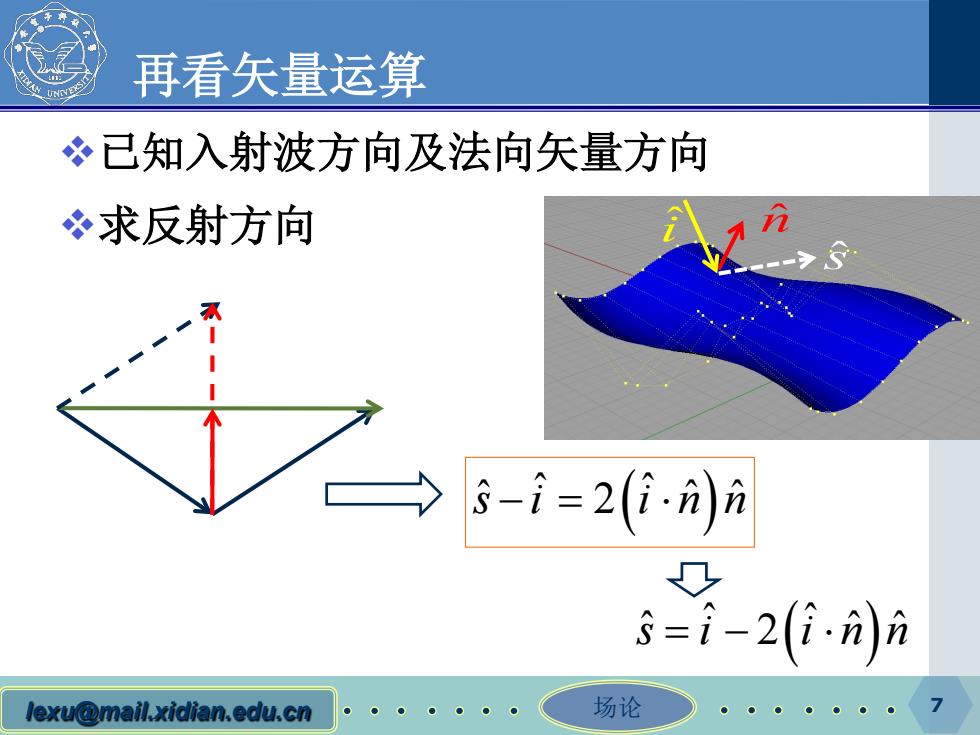
再看矢量运算 冬已知入射波方向及法向矢量方向 冬求反射方向 3-i=2() 5=i-2(i.in lexu@mail.xidian.edu.cn 场论
lexu@mail.xidian.edu.cn 场论 再看矢量运算 已知入射波方向及法向矢量方向 求反射方向 7 ( ) ˆ ˆ s i inn ˆ =− ⋅ 2 ˆ ˆ ˆ i n ˆ s ˆ ( ) ˆ ˆ s i inn ˆ −= ⋅ 2 ˆ ˆ

再看矢量运算 冬已知入射波方向及法向矢量方向 冬求垂直与入射面的切向方向 1=ixh lexu@mail.xidian.edu.cn 场论 8
lexu@mail.xidian.edu.cn 场论 再看矢量运算 已知入射波方向及法向矢量方向 求垂直与入射面的切向方向 8 ˆ i n ˆ t ˆ ˆ ˆ t in = × ˆ

再看矢量运算 冬试由牛顿定律证明能量守恒 F=ma d Fv- 0-42心)→方m-d lexu@mail.xidian.edu.cn 场论 9
lexu@mail.xidian.edu.cn 场论 再看矢量运算 试由牛顿定律证明能量守恒 9 F ma = dv F m dt = dv Fv m v dt = 1 2 2 d F v mv dt = F = 0 若 1 2 0 2 d mv dt = 1 2 =0 2 mv

再看矢量运算 麦克斯韦James Clerk Maxwel1831~1879)英国物理学家 16岁进入爱丁堡大学,后转入剑桥大学研习数学,毕业后留校任职。 1871年受聘为剑桥大学的实验物理学教授,负责筹建该校的第一所物 理学实验室一卡文迪许实验室,1874年建成后担任主任。1879年第 11月5日在剑桥逝世,终年只有49岁。 爱因斯坦在自传中说:“在我求学的时代,最吸引人的题目就是麦克 斯韦的理论”,“特殊的相对论起原于麦克斯韦的电磁场方程”。 1931年,在纪念麦克斯韦诞生100周年时,爱因斯坦把麦克斯韦的电 磁场贡献评价为“自牛顿时代”以来物理学所经历的最深刻最有成效 的变化。” 一位著名的现代物理学家曾感叹说:“麦克斯韦的思想是太不平常了, 甚至象亥姆霍兹和波耳兹曼这样有异常才能的人,为了理解它,也花 了几年的力气。” lexu@mail.xidian.edu.cn ●】 场论 10
lexu@mail.xidian.edu.cn 场论 再看矢量运算 麦克斯韦(James Clerk Maxwel 1831~1879)英国物理学家 16岁进入爱丁堡大学,后转入剑桥大学研习数学,毕业后留校任职。 1871年受聘为剑桥大学的实验物理学教授,负责筹建该校的第一所物 理学实验室——卡文迪许实验室,1874年建成后担任主任。1879年第 11月5日在剑桥逝世,终年只有49岁。 爱因斯坦在自传中说:“在我求学的时代,最吸引人的题目就是麦克 斯韦的理论”,“特殊的相对论起原于麦克斯韦的电磁场方程”。 1931年,在纪念麦克斯韦诞生100周年时,爱因斯坦把麦克斯韦的电 磁场贡献评价为“自牛顿时代”以来物理学所经历的最深刻最有成效 的变化。” 一位著名的现代物理学家曾感叹说:“麦克斯韦的思想是太不平常了, 甚至象亥姆霍兹和波耳兹曼这样有异常才能的人,为了理解它,也花 了几年的力气。” 10