
西安电子科枝大学 电子工程学院《D School of Electronic Engineering.Xidian University http://see xidian.edu.cn n.edu.cr 场论与复变函数 xuamail.x 主讲:徐乐 2011年11月6日星期日
lexu@mail.xidian.edu.cn

复数概论 复数 lexuamail.xidian.edu.cx ■复数的表示 复数的运算 ■复球面 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复数 ■为复变函数论的创建做了最早期工作的是欧拉、达朗 贝尔等先驱 ·而这门学科的发展作了大量奠基工作的是柯西、黎曼 和德国数学家维尔斯特拉斯。 ·从柯西算起,复变函数论已有170多年的历史了。它 以其完美的理论与精湛的技巧成为数学的一个重要组 成部分。它曾经推动过一些学科的发展,并且常常作 为一个有力的工具被应用在实际问题中,它的基础内 容已成为理工科很多专业的必修课程。 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复数 ■复变函数的应用涉及面很 odu. 。可以用来解决复杂的计算 ·物理学上有很多不同的稳定平面场,对它们的 计算就是通过复变函数来解决的。 。 俄国的茹柯夫斯基在设计飞机的时候,就用复 变函数论解决了飞机机翼的结构问题,他在运 用复变函数论解决流体力学和航空力学方面的 问题上也做出了贡献。 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复数 由三次方程求解公术m,V ■二次方程 x2+1=0 x.2=±V1 。实数域中无解 ,2=士 。引入虚数单位:,且: exu i=√ lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复数 ·对于任意两个实数x,y,称zx+yi为复数 ·x为复数z的实部,RE ·y为复数z的虚部,y=Im ·x=0,y0,则复数z=yi称为纯虚数; ·x0,y=0,则复数z=x成为实数: 。两个复数相等,必须且只须它们的实部和虚部 分别相等 x=0 z=x+yi=0 y=0 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复数的表示 般表示法 z=x+7 edu.c ·任意一个复数z都与一对实数(x,y)一一对应; ·任意一个复数z都与复平面上的点(x,y)一一对应 ■“数z”与“点z”同义 (x) ■以x轴为复平面的实轴 ■以y轴为复平面的虚轴 “数z也与从原点指向“点z”的平面向量一一对应 ·复平面一般标记为z平面或者w平面 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复数的表示 以几何语言和方法来研究复变函数可使其能够广 泛应用于实际 P(x,y) ■复数z与平面向量 Z=r= /r +v x≤z,y≤z zx +y 辐角 Argz=0 ig(Argz)= lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复数的表示 ■辐角 ·z0时,以正实轴为始边,表示z的向量为终边的角的 弧度称为z的辐角 ·z=0时,辐角不确定 。任何一个0时的复数,辐角无穷多 Ar82=0+2k元 ▣辐角主值 。在z(0)的辐角中,满足-π<0。≤π的8称为Argz的主值, 记作 argz lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
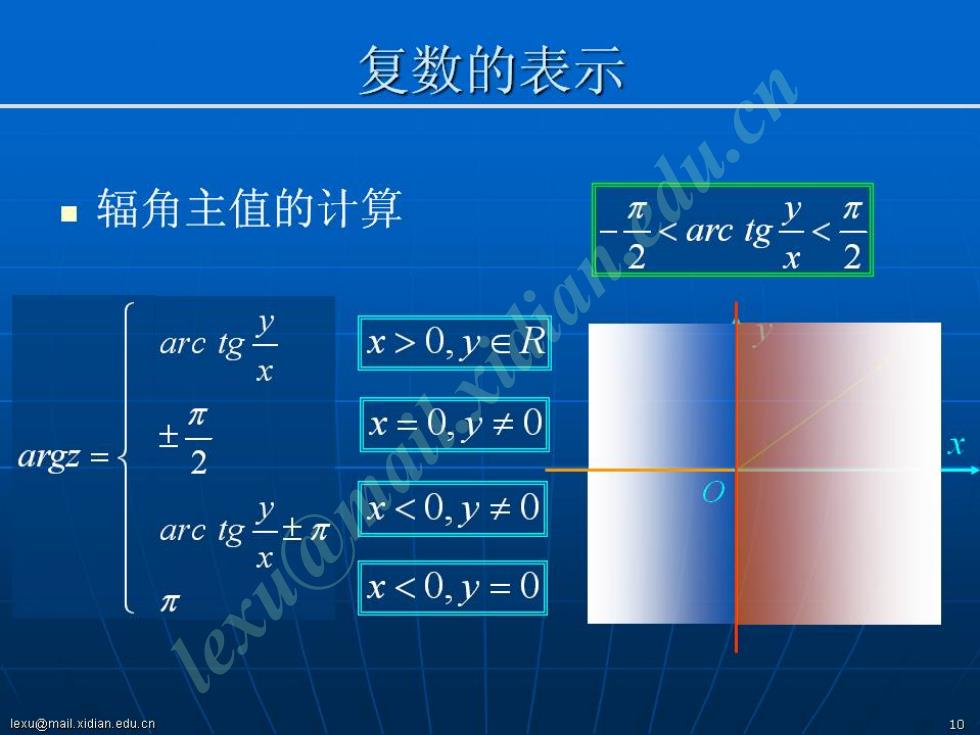
复数的表示 辐角主值的计算 V areg二0,y∈R x0,y≠0 argz 2 x<0,y≠0 arc tg之士元 π exu x<0,y=0 lexu@mail.xidian.edu.cn 10
lexu@mail.xidian.edu.cn