
市货龙子件枝大學 电子工程学院《A School of Electronic Engineering.Xidian University http://see .xidian.edu.cn n.edu.ch 场论与复变函数 xuamail.x 主讲:徐乐 2011年11月6日星期日
lexu@mail.xidian.edu.cn
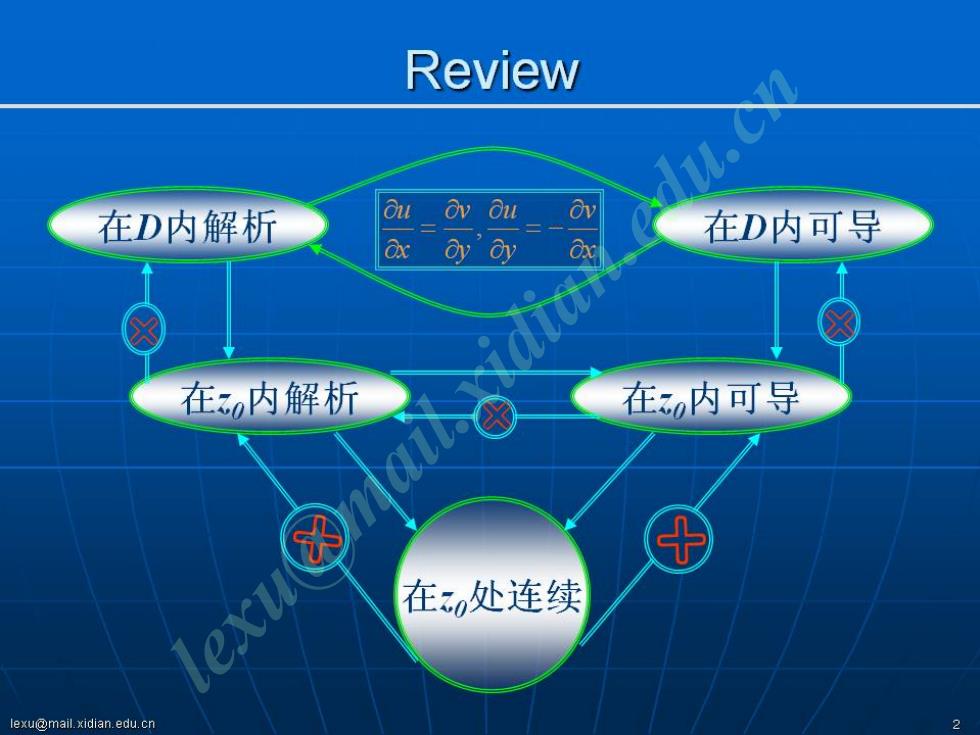
Review 在D内解析 Ou ov ou ov 在D内可导 ox ay oy 在3内解析 在内可导 在处连续 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

Review 下=yx+yy f)= ▣平面流速场的复势 f(=(x.v)+iv(x.v) ao(x,y) au(x,y) 0y,_0y=0 Ox Ox ot拉= divv= Ox Oy o(x,y) u(x,y) Cy E=E.x+EyE=-f'(②) ■静电场的复势 Ov E, ou Ex= rotE OE,E ax x =0 divE=OE=0 oy E ou Oy lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
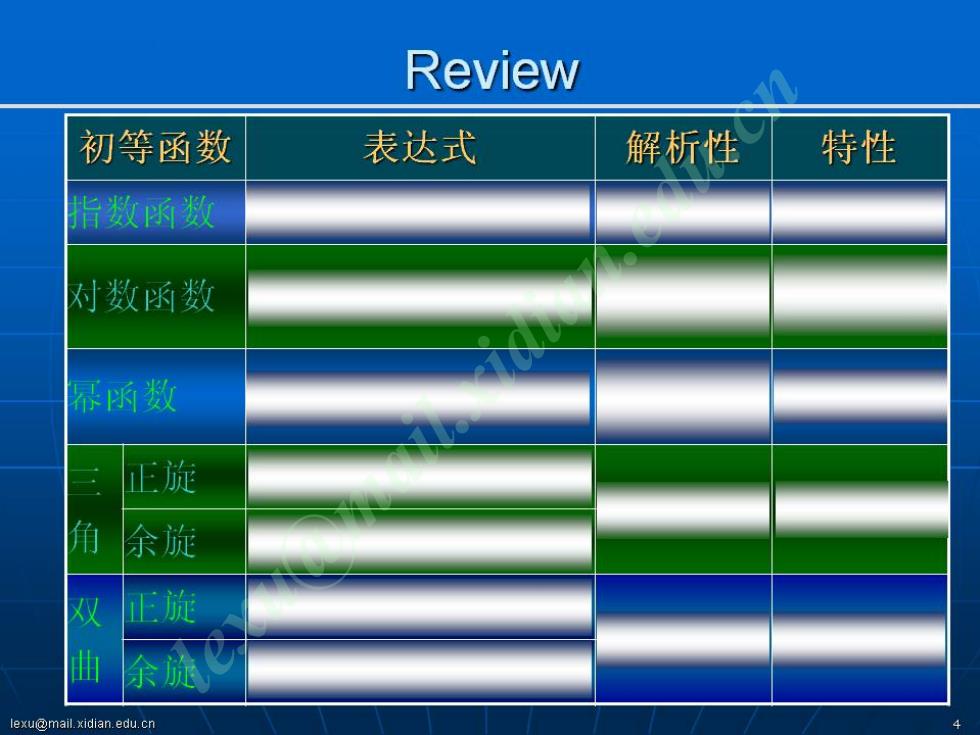
Review 初等函数 表达式 解析性 特性 指数函数 对数函数 幂函数 正旋 角 余旋 双 正旋 曲 余旋 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复变函数的积分 ·在微积分学中微分法和积分法是研究函数性质的重要方法 ■在复变函数中积分方法同微分方法一样也是研究复变函数 性质的方法,是解决实际问题的有力工具 设C为平面上给定的一条光滑(或按段光滑)曲线 ·选定C的两个可能方向中的个作为正方向(或正向),则曲线C 称为有向曲线 ·一若A、B为曲线C的两个端点,且从A到B的方向是C的正向,则A 为起点,B为终点 从B到A的方向就是C的负方向,记作C 。 若C是简单闭合曲线,则闭曲线正向是指当曲线上的点P沿该正向 前进时,P点左方的点总在曲线内部 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复变函数的积分 ■复变函数积分的定义: ·设函数z定义在区域D内 ·C为D内始于A终于B的光滑有向曲线 ·将曲线C任意分为n个弧段,其分点为: ■A=202122,…,2,22分B ·在每个弧段z到2上任取一点S,并作和式 是北八5:9 ·令△s,= ·当无限增加,且6趋于零时,若不论对C的分法及的 取法如何,S有唯一极限,则该极限称为函数fz)沿曲 线C的积分,记作: f)d-m>f(5.)As, lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复变函数的积分 ■Notel:若C为闭曲线,则沿此闭曲线的积分记作: ff)d= ■Note2:若C是实轴上的区间a≤x≤b,而fE=ux) 时,/复变函数的积分定义与一元时变函数 积分的定义相同 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复变函数的积分 ■积分存在的条件及计算方法 ·设光滑曲线C的参数方程为z)=xy),a≤孕 ·曲线C的正向为参数增加的方同 ·且z')≠0,a≤tB ·若f阳=u,+v,)在D内处处连续,则u,及v,以在 D内连续 ·令5+ne且△=△x+△y 三飞25m)+G:n,aF) k -∑a5,)△5,)+u5nAy+5n,)A lexu@mail.xidian.edu.cn Jof(=)d J。4(x,)d J。c,)d Jcu(x月d Jcv(x,y)dx
lexu@mail.xidian.edu.cn

复变函数的积分 fe)t=∫。k-d++ud ■Notel: 当复变函数)连续,曲线C光滑时,积分∫fe)正 定存在 a00 Note2: ∫fe)d可通过两个元实变函数线积分来计算 Note3: 若C是由C,C.,C等光滑曲线按段依次互 连构成的按段光滑曲线,则 fe)k6a)+fa)证++a)t ■Note4:对于沿参数形式描述曲线的复变函数积分 ∫fa)边=∫几z(y0d lexu@mail.xidian.edu.cn 若无特殊声明,总假定被积函数连续且曲线按段光滑
lexu@mail.xidian.edu.cn

复变函数的积分 et=几epe ■[证明] ∫fe)t=∫d-dtk+ud dx =x(t)dt dy =y'(t)dt fe)k台J'O-ydt+∫[x'o+']t 兰。(4+wx0+y']t J0p0d lexu@mail.xidian.edu.cn 10
lexu@mail.xidian.edu.cn