
1931 场论与复变函数 复变函数篇 主讲:徐乐
场论与复变函数 复变函数篇 主讲:徐乐

Review 冬复变函数的导数f) lim f(+△)-f(a) △-0 △ ·实变函数的求导法则可适用于复变函数,且证 法相同 复变函数的微分△w=f'()△+p(△)△ ·f亿d△z为函数在w=f(点z的微分 解析函数 ·[定义]若函数f(在z及z的邻域内处处可导, 则称函数f(在z解析 lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn ●●●●●● 2
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 2 Review 复变函数的导数 实变函数的求导法则可适用于复变函数,且证 法相同 复变函数的微分 f ‘(z0) △z为函数在w=f (z)点z0的微分 解析函数 [定义]若函数f (z)在z0及z0的邻域内处处可导, 则称函数f (z)在z0解析 0 0 0 0 0 ( ) () '( ) lim z z z dw fz z fz f z dz z ∆ → = +∆ − = = ∆ 0 ∆ = ∆+ ∆ ∆ w fz z zz '( ) ( ) ρ
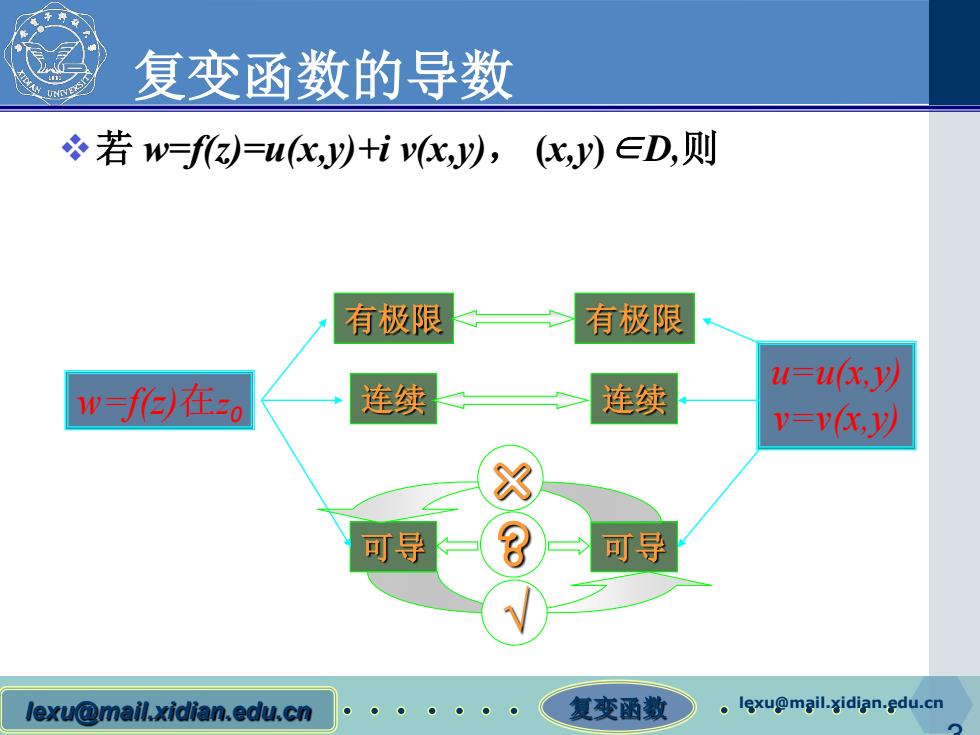
复变函数的导数 若w=f)=u,以+iK,以,(,y)∈D,则 有极限 有极限 1=u,y以 w=fe在o 连续 连续 =vx,以 X 可导 可导 lexu@mail.xidian.edu.cn 复变函数 .lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 3 复变函数的导数 若 w=f(z)=u(x,y)+i v(x,y), (x,y)∈D,则 w=f(z)在z0 有极限 连续 可导 u=u(x,y) v=v(x,y) 有极限 连续 ? 可导 √ ×

解析函数 定理1):f(、g)在区域D解析,则其四则运算 (除去分母为零的点外的商)在D内解析 冬定理2):复合函数的解析性质: ·设函数h=g)在z平面上的区域D内解析 ·设函数w=f(h)在h平面上的区域G内解析 ·若对D内每一点z,函数g(d对应值h都属于G,则复合 函数w=fg(/在D内解析 lexu@mail.xidian.edu.cn 复变函数 .lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 4 解析函数 定理1):f (z)、g (z)在区域D解析,则其四则运算 (除去分母为零的点外的商)在D内解析 定理2):复合函数的解析性质: 设函数h=g (z)在z平面上的区域D内解析 设函数w=f (h)在h平面上的区域G内解析 若对D内每一点z0,函数g (z)对应值h都属于G,则复合 函数w=f [g (z)]在D内解析

解析函数 在D内解析 在D内可导 在z内解析 在z内可导 入 在z处连续 lexu@mail.xidian.edu.cn 复变函数 .lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 5 解析函数 在D内解析 在D内可导 在z0内解析 在z0内可导 在z0处连续 × × ×

解析函数 冬[思考]若函数w=f(=u化y)+ivky)可导 化y)、v化,y)有什么性质? ·函数w=f)=K)+ivK)在区域D内一点zx+y可导的必 要条件 Ou ov Cauchy-Riemann方程 柯西-黎曼方程 ou 0 ay 8x lexu@mail.xidian.edu.cn 复变函数 .lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 6 解析函数 [思考]若函数w= f (z)= u(x,y)+i v(x,y) 可导 u(x,y)、v(x,y)有什么性质? 函数w= f (z)= u(x,y)+i v(x,y)在区域D内一点z=x+iy可导的必 要条件 u v x y u v y x ∂ ∂ = ∂ ∂ ∂ ∂ = − ∂ ∂ Cauchy-Riemann方程 柯西-黎曼方程

解析函数 冬定理一复变函数在一点处可导的充要条件 ·函数f)=uKy)+ic)在区域D内 ·函数f)在D内一点z=x+y可导的充要条件 ·u化,y)和v,y)在点(化,y)可微 ·且在该点满足柯西黎曼方程 ay'oy 0 必要性已证,充分性有待证明 lexu@mail.xidian.edu.cn ●● 复变函数 .lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 7 解析函数 定理一 复变函数在一点处可导的充要条件 函数f (z)= u(x,y)+i v(x,y)在区域D内 函数f (z)在D内一点z=x+iy可导的充要条件 • u(x,y)和v(x,y)在点(x,y)可微 • 且在该点满足柯西-黎曼方程 , u vu v x yy x ∂ ∂∂ ∂ = = − ∂ ∂∂ ∂ 必要性已证,充分性有待证明

第10进解析函数 (I) 冬解析函数的充要条件 冬平面场的复势 lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 8 第10讲 解析函数(II) 解析函数的充要条件 平面场的复势

解析函数的充要条件 冬可导函数的充要条件 ·定理一复变函数在一点处可导的充要条件 ·函数f)=uK)+i比y)在区域D内 ·函数f在D内一点z=x+y可导的充要条件 -u化y)和v化,y)在点(化,y)可微 且在该点满足柯西黎曼方程 ov ou a oy'oy Ox 必要性已证,充分性有待证明 lexu@mail.xidian.edu.cn 复变函数 lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 9 解析函数的充要条件 可导函数的充要条件 定理一 复变函数在一点处可导的充要条件 • 函数f (z)= u(x,y)+i v(x,y)在区域D内 • 函数f (z)在D内一点z=x+iy可导的充要条件 – u(x,y)和v(x,y)在点(x,y)可微 – 且在该点满足柯西-黎曼方程 , u vu v x yy x ∂ ∂∂ ∂ = = − ∂ ∂∂ ∂ 必要性已证,充分性有待证明
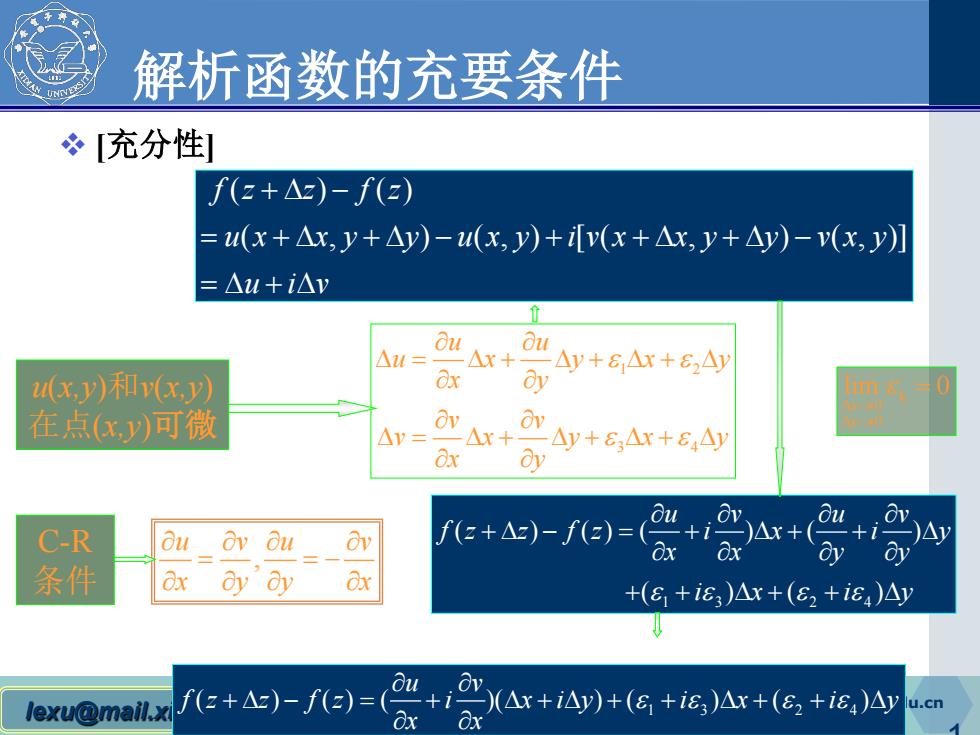
解析函数的充要条件 充分性 f(z+△z)-f(z) =u(x+△x,y+y)-u(x,y)+v(x+△x,y+△y)-v(x,y] =△l+i△y △M= 04 △+ Ou △y+6,△x+6,△y 4(y)和() Ox a 在点)可微 △v=OAr+0y+E,Ar+EAy Ox oy C-R Ou (i) oy'"Oy 条件 dy oy +(G,+ie,)△x+(82+ie4)△y lexu@mail.xi f(2+△)-f(z)=(G -+i- )(△x+i△y)+(e,+ie)Ax+(E2+ie4)Ay lu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 1 解析函数的充要条件 [充分性] ( ) () ( , ) ( , ) [ ( , ) ( , )] fz z fz u x x y y u x y ivx x y y vx y u iv +∆ − = +∆ +∆ − + +∆ +∆ − =∆ + ∆ u(x,y)和v(x,y) 在点(x,y)可微 1 2 3 4 u u u x yxy x y v v v x yxy x y ε ε ε ε ∂ ∂ ∆ = ∆+ ∆+ ∆+ ∆ ∂ ∂ ∂ ∂ ∆= ∆+ ∆+ ∆+ ∆ ∂ ∂ k 0 0 lim 0 x y ε ∆ → ∆ → = 13 24 ( ) () ( ) ( ) ( )( ) uv uv fz z fz i x i y xx yy εε εε ix iy ∂∂ ∂∂ +∆ − = + ∆ + + ∆ ∂∂ ∂∂ + + ∆+ + ∆ , u vu v x yy x ∂ ∂∂ ∂ = = − ∂ ∂∂ ∂ C-R 条件 13 24 ( ) ( ) ( )( ) ( ) ( ) u v fz z fz i x iy i x i y x x εε εε ∂ ∂ +∆ − = + ∆ + ∆ + + ∆ + + ∆ ∂ ∂