
1931 场论与复变函数 主讲:徐乐 2013/10/13
lexu@mail.xidian.edu.cn 复变函数 2013年10月13日星期日 2013/10/13 主讲:徐乐 场论与复变函数

画 Review 冬解析函数的充要条件 ·函数f=uc,y)+iK,y)在区域D内 ·uc,y)和v化,y)在区域D可微 ·且在区域D满足柯西黎曼方程 ·[推论1]若f(在区域D处处为零,则Pa在D内为常数 ·[推论2f(=uKy)+iv,y)为解析函数,且f()≠0, 则曲线族u化以=cp化以=c2必互相正交,其中 Cc2为常数 .exH@mailxidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 2 Review 解析函数的充要条件 • 函数f (z)= u(x,y)+i v(x,y)在区域D内 • u(x,y)和v(x,y)在区域D可微 • 且在区域D满足柯西-黎曼方程 [推论1]若f’(z) 在区域D处处为零,则f’(z)在D内为常数 [推论2] f (z)= u(x,y)+i v(x,y)为解析函数,且f’(z)≠0 , 则曲线族u(x,y)=c1,v(x,y)=c2必互相正交,其中 c1, c2为常数
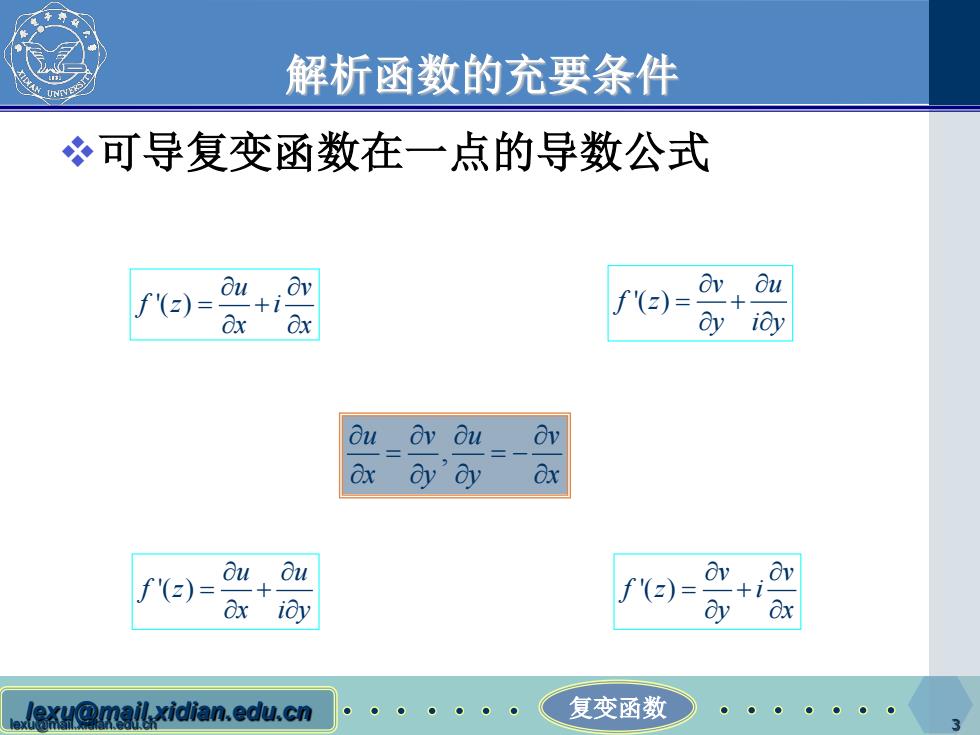
解析函数的充要条件 冬可导复变函数在一点的导数公式 ou, Ov ou f(z))= +1 f'(z)= + u Ov Ou 8x dy'ay 8x Ou u f'(z)= f'(z)= 8x ioy ay Ox lexy@mailxidian.edu.cn 复变函数 ●● ●
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 3 解析函数的充要条件 可导复变函数在一点的导数公式 '( ) u v fz i x x ∂ ∂ = + ∂ ∂ , u vu v x yy x ∂ ∂∂ ∂ = = − ∂ ∂∂ ∂ '( ) v u f z y iy ∂ ∂ = + ∂ ∂ '( ) u u f z x iy ∂ ∂ = + ∂ ∂ '( ) v v fz i y x ∂ ∂ = + ∂ ∂
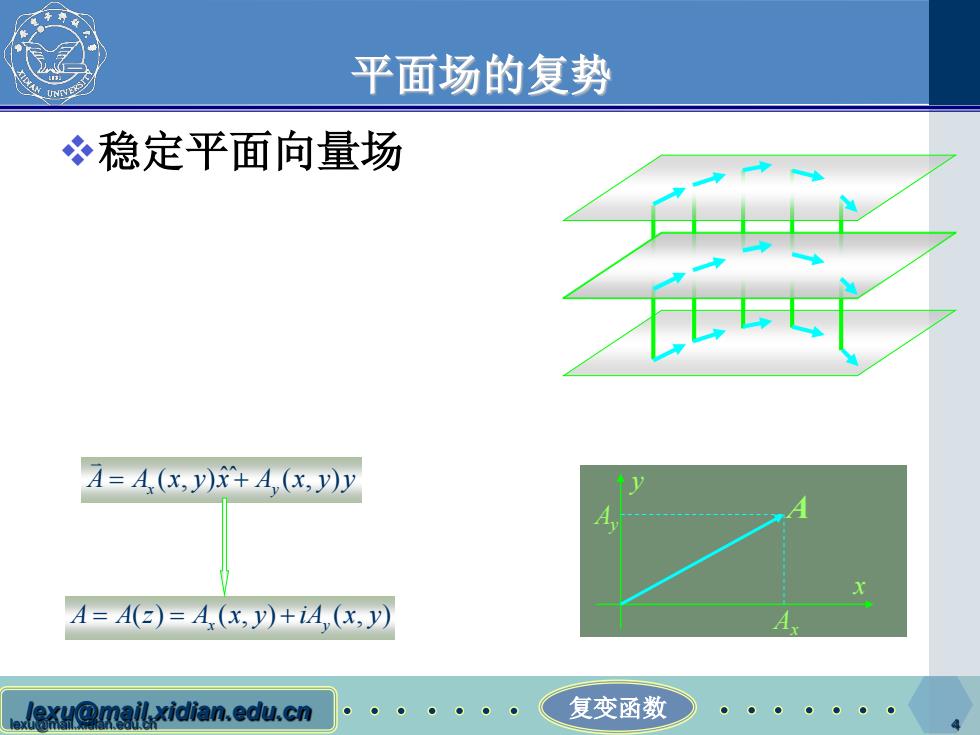
平面场的复势 冬稳定平面向量场 A=A(x,y)A,(x,y)y A=A()=A.(x,y)+iA,(x,y) xH@mailxidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 4 平面场的复势 稳定平面向量场 x y A A y Ax (, ) (, ) ˆˆ A A xyx A xyy = + x y () (, ) (, ) A A z A x y iA x y = = + x y
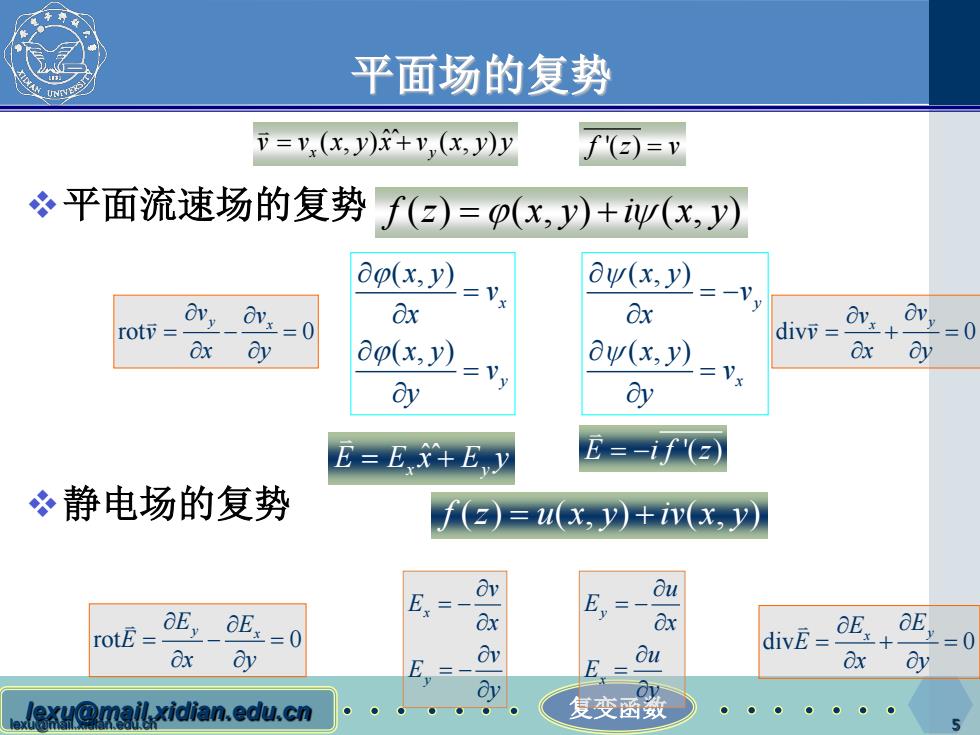
平面场的复势 V=v,(x,y)x+v,(x,y)y f()=v 冬平面流速场的复势 f(2)=o(x,y)+iv(x,y) ao(x,y) Vx au(x,y) roti= vx二0 Ox 0x divv +=0 8x dy do(x,y) 二Vy ou(x,y) 8x Oy 8y V: E=,y E=-if() 冬静电场的复势 )=u(x,y)+iv(x,v) Ex=- Ov ou otEs」 E aE:=0 8x Ox Ov ou div= E E, =0 Ox oy E ex@mailxidian.edu.cn 复变函数 ●
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 5 平面场的复势 平面流速场的复势 静电场的复势 (, ) (, ) ˆˆ x y v v xyx v xyy = + (, ) (, ) x y x y v x x y v y ϕ ϕ ∂ = ∂ ∂ = ∂ div 0 x y v v v x y ∂ ∂ =+= ∂ ∂ (, ) (, ) y x x y v x x y v y ψ ψ ∂ = − ∂ ∂ = ∂ rot 0 y x v v v x y ∂ ∂ =−= ∂ ∂ f z xy i xy () (, ) (, ) = + ϕ ψ fz v '( ) = ˆˆ E Ex Ey = + x y rot 0 y x E E E x y ∂ ∂ =−= ∂ ∂ x y v E x v E y ∂ = − ∂ ∂ = − ∂ div 0 E x E y E x y ∂ ∂ =+= ∂ ∂ y x u E x u E y ∂ = − ∂ ∂ = ∂ f z u x y iv x y () (, ) (, ) = + E if z = − '( )

初等函数 指数函数 冬对数函数 必乘幂与幂函数 冬三角函数和双曲函数 冬反三角函数和反双曲函数 .xH@maixidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 6 初等函数 指数函数 对数函数 乘幂与幂函数 三角函数和双曲函数 反三角函数和反双曲函数

初等函数 初等函数 ·在微积分的发展史上,有一些函数很早就被人们所认 识并且进行了深入的研究,这些函数统称为初等函数 ·最基础的初等函数称为基本初等函数 ·常值函数、幂函数、指数函数、对数函数、三角函数、反三角 函数 ·凡是由基本初等函数经过有限次四则运算和有限次复 合步骤得到的,并能用一个解析式表示的函数统称为 初等函数。 ·复变函数初等函数是实变函数初等函数的推广 le然M@ailxidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 7 初等函数 初等函数 在微积分的发展史上,有一些函数很早就被人们所认 识并且进行了深入的研究,这些函数统称为初等函数 最基础的初等函数称为基本初等函数 • 常值函数、幂函数、指数函数、对数函数、三角函数、反三角 函数 凡是由基本初等函数经过有限次四则运算和有限次复 合步骤得到的,并能用一个解析式表示的函数统称为 初等函数。 复变函数初等函数是实变函数初等函数的推广

指数函数 必 在实变函数中,指数函数e对任何实数x 都可导,且(e)'=er 在复平面中定义函数f(),使得 i.f(z)在复平面内处处解析 ii.f(z)=f(a) V ii.Im(☑=0时,f(z)=e,其中x=Re(z) 验证函数f(z)=er(cosy+isiny) .xHmaixidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 8 指数函数 在实变函数中,指数函数ex对任何实数x 都可导,且(ex)’=ex 在复平面中定义函数f (z),使得 i. f (z)在复平面内处处解析 ii. f’ (z) = f (z) iii. Im(z) = 0时,f (z) =ex,其中x=Re(z) 验证函数 f (z)= ex(cosy +isiny)

指数函数 冬指数函数 ·指数函数记作expz=e(cosy+isiny) ·指数函数的等价定义 ·|expz=er ·Arg(expz)=y+2km ■Notel:exp(z)≠0 -Note2:exp(1)exp(z2)=exp(1+z2) exH@mailxidian.edu.cn 复变函数 ●
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 9 指数函数 指数函数 指数函数记作 expz =ex (cosy +isiny) 指数函数的等价定义 • | expz |=ex • Arg(expz)= y + 2 kπ Note1:exp(z) ≠ 0 Note2: exp(z1)exp(z2)=exp(z1+z2)

指数函数 Note3:为方便,令e=expz ·ez仅为表示指数函数的符号,无幂的意义 Note4:x=0时,e=(cosy+isiny) Note5:周期性:ez+i2km=e 周期为2kπi 复变函数的指数函数具有周期性,而实变函数 e没有周期性 xH@mailxidian.edu.cn 复变函数 10
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 10 指数函数 Note3:为方便,令 ez = expz • ez 仅为表示指数函数的符号,无幂的意义 Note4:x=0时, eiy =(cosy +isiny) Note5:周期性: ez+i2kπ= ez • 周期为2kπi 复变函数的指数函数具有周期性,而实变函数 ex没有周期性