
《数学教学论》教学大纲 课程编码:1511108002 课程名称:数学教学论 学时/学分:32/2 先修课程:《教育学》、《心理学》 适用专业:数学与应用数学专业 开课教研室:课程论教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的专业必修课。 2.课程任务:本课程是一门与数学、教有学、心理学、逻辑学、数学数学论等学科相 关联的综合性、边缘性学科,同时也是一门实践性很强的学科。通过本课程的学习,使学生 了解数学教育发展的历史和现状,掌握中学数学教育的基本理论和方法以及中学数学概念 命题、解题教学的基本方法和技能,理解中学数学课程的制定与改革的历史与现状,具备应 用中学数学教有理论和方法于中学数学教学实践的能力,提高中学数学教有研究的能力,学 生扩大数学视野,培养数学思维品质,克服对中学数学教学工作的畏难心理,激发学习兴趣。 二、课程教学基本要求 明确在中学数学教学中“怎样教”、“怎样学”、“怎样评”和“教什么”、“学什么”以及 相关的理论和实践,帮助学生树立先进的教学理念,掌握数学教学的基本规律和教学技能以 及教学研究方法,培养未来数学教师的基本本领。为后续的微格教学、初等数学研究课程提 供必要的理论和方法学支持。主要教学环节包括课堂讲授、案例分析、小组讨论等。其中以 课堂讲授为主,研制电子教案和多媒体幻灯片以及C!课件,在教学方法和手段上采用现 代教育技术。 成绩考核形式:期终成绩(闭卷考试)(70%)+平时成绩(平时测验、作业、课堂提问、 课堂讨论等)(30%)。成绩评定采用百分制,60分为及格。 三、课程教学内容 第一章绪论 1.教学基本要求 理解和掌握数学教学论的定义和研究范围,明确数学教学论的学科性质:掌握数学教学 论的研究方法。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能准确理解数学教学论、观察法、实验法、调查法、访谈法
《数学教学论》教学大纲 课程编码:1511108002 课程名称: 数学教学论 学时/学分:32/2 先修课程:《教育学》、《心理学》 适用专业:数学与应用数学专业 开课教研室:课程论教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的专业必修课。 2.课程任务:本课程是一门与数学、教育学、心理学、逻辑学、数学数学论等学科相 关联的综合性、边缘性学科,同时也是一门实践性很强的学科。通过本课程的学习,使学生 了解数学教育发展的历史和现状,掌握中学数学教育的基本理论和方法以及中学数学概念、 命题、解题教学的基本方法和技能,理解中学数学课程的制定与改革的历史与现状,具备应 用中学数学教育理论和方法于中学数学教学实践的能力,提高中学数学教育研究的能力,学 生扩大数学视野,培养数学思维品质,克服对中学数学教学工作的畏难心理,激发学习兴趣。 二、课程教学基本要求 明确在中学数学教学中“怎样教”、“怎样学”、“怎样评”和“教什么”、“学什么”以及 相关的理论和实践,帮助学生树立先进的教学理念,掌握数学教学的基本规律和教学技能以 及教学研究方法,培养未来数学教师的基本本领。为后续的微格教学、初等数学研究课程提 供必要的理论和方法学支持。主要教学环节包括课堂讲授、案例分析、小组讨论等。其中以 课堂讲授为主,研制电子教案和多媒体幻灯片以及 CAI 课件,在教学方法和手段上采用现 代教育技术。 成绩考核形式:期终成绩(闭卷考试)(70%)+平时成绩(平时测验、作业、课堂提问、 课堂讨论等)(30%)。成绩评定采用百分制,60 分为及格。 三、课程教学内容 第一章 绪 论 1.教学基本要求 理解和掌握数学教学论的定义和研究范围,明确 数学教学论的学科性质;掌握数学教学 论的研究方法。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能准确理解数学教学论 、 观察法、 实验法、调查法、访谈法

等基本概念,掌握数学教学论学的研究方法。 3.教学重点和难点 重点:数学教有成为一个专业、 一门科学学科的历史,数学教有学的研究方法。 难点:数学教有学的研究方法。 4.教学内容 第一节数学教育成为一个学科的历史 L.数学教育的定义 2.数学教育学的研究范围 3.数学教有学成为一个专业的历史 4.数学教有成为一门科学学科的历史 5.数学教有研究热点的演变 第二节几个数学教育研究的案例 1.案例1-通过访谈了解学生的想法实践篇 2.案例2-观察一堂以师生问答为主的课 3.案例3-通过教学实验检验理论 4.案例4-对教师课堂教学用语的调查研究 第二章与时俱进的数学教育 1.教学基本要求 了解当前数学教有的发展趋势,理解新课程改革的背景,以及数学教有课程改革 的动态。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能准确理解数数学文化、数学探究和数学应用的概念 3.教学重点和难点 重点:深入了解改革中的中国数学教育. 难点:理解并能够分析近现代数学教育的几个重大事件。 4.教学内容 第一节20世纪数学观的变化 1.数学不等于逻辑 2.数学不等于形式 3.注重数学的应用性 4.注重数学的文化价值 第二节作为社会文化的数学教育 1.数学是人类文明的火车头
等基本概念,掌握数学教学论学的研究方法。 3.教学重点和难点 重点:数学教育成为一个专业、一门科学学科的历史,数学教育学的研究方法。 难点:数学教育学的研究方法。 4.教学内容 第一节 数学教育成为一个学科的历史 1.数学教育的定义 2.数学教育学的研究范围 3.数学教育学成为一个专业的历史 4.数学教育成为一门科学学科的历史 5.数学教育研究热点的演变 第二节 几个数学教育研究的案例 1.案例1-通过访谈了解学生的想法实践篇 2.案例2-观察一堂以师生问答为主的课 3.案例3-通过教学实验检验理论 4.案例4-对教师课堂教学用语的调查研究 第二章 与时俱进的数学教育 1.教学基本要求 了解当前数学教育的发展趋势,理解新课程改革的背景,以及数学教育课程改革 的动态。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能准确理解数数学文化、数学探究和数学应用的概念。 3.教学重点和难点 重点:深入了解改革中的中国数学教育。 难点:理解并能够分析近现代数学教育的几个重大事件。 4.教学内容 第一节 20世纪数学观的变化 1.数学不等于逻辑 2.数学不等于形式 3.注重数学的应用性 4.注重数学的文化价值 第二节 作为社会文化的数学教育 1.数学是人类文明的火车头

2.数学打上了各个文化发展阶段的烙印 3.数学应从社会文化中汲取营养 4.数学思维方式对人类文化的独特贡前 5,数学成为描述社会和自然的语言 第三节20世纪我国数学教育观的变化 1.由关心教师的教转向关注学生的学 2.从双基与三大能力观点的形成,发展到更宽广的能力关和素质关 3.从听课、阅读、演题,到提倡实验、讨论、探索的学习方式 4.从看重数学的抽象严革,到关注数学文化、数学探究和数学应用 第四节国际视野下的中国数学教育 1.第十届国际数学家大会课题研究组的主题 2.第十届国际数学家大会课题讨论组的主题 第五节改革中的中国数学教育 1.教育受到空前的重视 2.数学素质教育需要解决的问题 3.基础教育数学课程改革不断深入 4.高等师范院校面临新的挑战 第三章数学教育的基本理论 1.教学基本要求 对数学教有有更深入的认识和理解,为课程学习奠定理论基础,并自觉应用于后继 的学习和指导中学数学教学。 2.要求学生掌握的基本概念、理论, 通过本章学习,使学生能够理解弗赖登塔尔的数学教有理论,波利亚的解题理论,建构 主义的数学教育理论,掌握数学双基的概念。 3.教学重点和难点 重点:理解弗赖登塔尔的数学教育理论,波利亚的解题理论,建构主义的数学教育理 论。 难点:建构主义理论关于数学教有的一些基本认识:对我国双基数学教学辩证理解, 4.教学内容 第一节弗赖登塔尔的数学教育理论 1.现实 2.数学化 3.再创造
2.数学打上了各个文化发展阶段的烙印 3.数学应从社会文化中汲取营养 4.数学思维方式对人类文化的独特贡献 5.数学成为描述社会和自然的语言 第三节 20世纪我国数学教育观的变化 1.由关心教师的教转向关注学生的学 2.从双基与三大能力观点的形成,发展到更宽广的能力关和素质关 3.从听课、阅读、演题,到提倡实验、讨论、探索的学习方式 4.从看重数学的抽象严谨,到关注数学文化、数学探究和数学应用 第四节 国际视野下的中国数学教育 1.第十届国际数学家大会课题研究组的主题 2.第十届国际数学家大会课题讨论组的主题 第五节 改革中的中国数学教育 1.教育受到空前的重视 2.数学素质教育需要解决的问题 3.基础教育数学课程改革不断深入 4.高等师范院校面临新的挑战 第三章 数学教育的基本理论 1.教学基本要求 对数学教育有更深入的认识和理解,为课程学习奠定理论基础,并自觉应用于后继 的学习和指导中学数学教学。 2.要求学生掌握的基本概念、理论。 通过本章学习,使学生能够理解弗赖登塔尔的数学教育理论,波利亚的解题理论,建构 主义的数学教育理论,掌握数学双基的概念。 3.教学重点和难点 重点:理解弗赖登塔尔的数学教育理论,波利亚的解题理论,建构主义的数学教育理 论。 难点:建构主义理论关于数学教育的一些基本认识;对我国双基数学教学辩证理解。 4.教学内容 第一节 弗赖登塔尔的数学教育理论 1.现实 2.数学化 3.再创造

第二节波利亚的解题理论 1.波利亚的数学教有观 2.波利亚关于解题的研究 第三节建构主义的数学教育理论 1.什么是数学知识? 2.什么是数学理解? 3.儿童如何学习数学 4.教师如何开展课堂教学? 5.谨慎地吸收建构这样的合理成分 第四节我国“双基”数学教学 1.数学双基和数学双基教学 2.我国双基数学教学的四个特在 3.数学双基教学的基本策略 4.将双基发展为四基 第四章 数学课程的制定与改革 1.教学基本要求 了解中外课程改革的历史和趋势,把握《全日制义务教育数学课程标准和普通高中数学 课程标准》的基本理念,为教育实践奠定思想指导基础。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解课程标准的概念,理解普通高中数学课程标准的基本理 念 3.教学重点和难点 重点:《普通高中数学课程标准》的基本理念。 难点:《普通高中数学课程标准》的基本理念。 4.教学内容 第一节中外数学课程改革简史 1.20世纪20年代之前的数学课程 2.20世纪20年代之前-1949年的数学课程 3.1949年-20世纪60、70年代的数学课程 4.20世纪80年代的数学课程 5.21世纪的数学课程 笔一书 《全日制义务教育数学课程标准》的制订与实验 1.数学课程标准的出现是改革开放的产物
第二节 波利亚的解题理论 1.波利亚的数学教育观 2.波利亚关于解题的研究 第三节 建构主义的数学教育理论 1.什么是数学知识? 2.什么是数学理解? 3.儿童如何学习数学? 4.教师如何开展课堂教学? 5.谨慎地吸收建构这样的合理成分 第四节 我国“双基”数学教学 1.数学双基和数学双基教学 2.我国双基数学教学的四个特征 3.数学双基教学的基本策略 4.将双基发展为四基 第四章 数学课程的制定与改革 1.教学基本要求 了解中外课程改革的历史和趋势,把握《全日制义务教育数学课程标准和普通高中数学 课程标准》的基本理念,为教育实践奠定思想指导基础。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解课程标准的概念,理解普通高中数学课程标准的基本理 念。 3.教学重点和难点 重点: 《普通高中数学课程标准》的基本理念。 难点:《普通高中数学课程标准》的基本理念。 4.教学内容 第一节 中外数学课程改革简史 1.20 世纪 20 年代之前的数学课程 2.20 世纪 20 年代之前-1949 年的数学课程 3.1949 年-20 世纪 60、70 年代的数学课程 4.20 世纪 80 年代的数学课程 5.21 世纪的数学课程 第二节 《全日制义务教育数学课程标准》的制订与实验 1.数学课程标准的出现是改革开放的产物

2.数学内容上的改革 3.数学学习方式和教学方法的改革,使学习内容的呈现发生变化 第三节《普通高中数学课程标准》 1.《普通高中数学课程标准》课程目标 2.《普通高中数学课程标准》基木理念 3.《普通高中数学课程标准》课程结构 第五章数学教育的核心内容 1.教学基本要求 对数学教有的基本问题有深入的认识和理解,为课程学习奠定理论基础,并自觉应 用于后继的学习和指导中学数学教学。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解数学教育目标、数学能力、数学教学模式、数学活动 经验的概念。 3.教学重点和难点 重点:数学教育目标的确定,数学教学模式 难点:数学教育目标的确定。 4.教学内容 第一节数学教育目标的确定 1.数学教有的基本功能 2.我国20世纪数学教有目标的变迁 3.确定中学数学教有目标的主要依据 第二节数学教学原则 1.一般数学教学原则 2.数学教学原则体系的构建 3.数学教学原则 第三节数学知识的教学 1.数学概念的教学 2.数学命题的教学 第四节数学能力的界定 1.什么是数学能力 2.数学能力观的变化 第五节数学思想方法的教学
2.数学内容上的改革 3.数学学习方式和教学方法的改革,使学习内容的呈现发生变化 第三节 《普通高中数学课程标准》 1.《普通高中数学课程标准》课程目标 2.《普通高中数学课程标准》基本理念 3.《普通高中数学课程标准》课程结构 第五章 数学教育的核心内容 1.教学基本要求 对数学教育的基本问题有深入的认识和理解,为课程学习奠定理论基础,并自觉应 用于后继的学习和指导中学数学教学。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解数学教育目标 、数学能力 、数学教学模式、数学活动 经验的概念。 3.教学重点和难点 重点:数学教育目标的确定,数学教学模式。 难点:数学教育目标的确定。 4.教学内容 第一节 数学教育目标的确定 1.数学教育的基本功能 2.我国 20 世纪数学教育目标的变迁 3.确定中学数学教育目标的主要依据 第二节 数学教学原则 1.一般数学教学原则 2.数学教学原则体系的构建 3.数学教学原则 第三节 数学知识的教学 1.数学概念的教学 2.数学命题的教学 第四节 数学能力的界定 1.什么是数学能力 2.数学能力观的变化 第五节 数学思想方法的教学

1.基本的数学思想方法 2.数学特有的方法 第六节数学活动经验 1.基本的数学活动经验 2.基木的数学活动经验的类型: 第七节数学教学模式 1.基本的数学教学模式 2.当前我国数学教学模式发展的趋势 第六章数学课堂教学观靡与评析 1.教学基本要求 体会“数学”与“数学教学”的区别和联系,增强教学意识;初步理解特定类型的课例 所反映出来的教学理念及教学方式。 2.要求学生掌握的基本概念、理论 通过木章学习,使学生能初步了解教学设计、活动教学、探究式教学等概念。 3.教学重点和难点 重点:对中学数学课堂怎样教学进入理论思考 4.教学内容 第一节师范生走向课堂执教时的困惑 1.教学片断实录(四个) 2.教学片断实录点评 第二节案例学习一数学弄懂了还要知道怎么教 1.概念教学一“代数式”的教学 2.命题教学一“三角函数”的图像变换的教学 3.定理教学一“梯形中位线定理”的教学 4.复习课的教学一“均值不等式”的复习课 第三节一些特定类型的课例赏析 1.活动教学 2.生成式的数学概念教学 3.整体数学教学 4.基于网络环境的数学教学 5.探究命题教学 6.探究性复习课 第四节一些案例(课堂教学片段)评析
1.基本的数学思想方法 2.数学特有的方法 第六节 数学活动经验 1.基本的数学活动经验 2.基本的数学活动经验的类型; 第七节 数学教学模式 1.基本的数学教学模式; 2.当前我国数学教学模式发展的趋势 第六章 数学课堂教学观摩与评析 1.教学基本要求 体会“数学”与“数学教学”的区别和联系,增强教学意识;初步理解特定类型的课例 所反映出来的教学理念及教学方式 。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能初步了解教学设计、活动教学、探究式教学等概念。 3.教学重点和难点 重点:对中学数学课堂怎样教学进入理论思考。 4.教学内容 第一节 师范生走向课堂执教时的困惑 1.教学片断实录(四个) 2.教学片断实录点评 第二节 案例学习—数学弄懂了还要知道怎么教 1.概念教学—“代数式”的教学 2.命题教学—“三角函数”的图像变换的教学 3.定理教学--“梯形中位线定理”的教学 4.复习课的教学--“均值不等式”的复习课 第三节 一些特定类型的课例赏析 1.活动教学 2.生成式的数学概念教学 3.整体数学教学 4.基于网络环境的数学教学 5.探究命题教学 6.探究性复习课 第四节 一些案例(课堂教学片段)评析

1.同一例题的不同命运 2.为什么扣两分? 3.荒唐的假设 4.i的意义是什么? 第七章数学教学设计 1.教学基本要求 领会数学教学设计的指导思想,编制数学教学目标的要求以及设计意图的形成工过程, 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解教学设计、教案。教学目标的概念。 3.教学重点和难点 重点:数学教学设计意图的形成:难点:形成形成有创意的数学教学设计。 4.教学内容 第一节教案三要素 1.教学设计及教案三要素 2.教学设计案例讲评 第二节数学教学目标的确定 1.远期目标 2.近期日标 3.过程性目标 第三节设计意图的形成 1.数学问题的教学设计 2.数学概念的教学设计 3.数学命题的教学设计 4.数学知识应用的教学设计 5.巩固课的教学设计 第四节教学过程的展示 1.设计意图的形成 2.优秀创意设计举 第八章数学研究的一些特定课题 1.教学基本要求 对数学教有研究的特殊领域数学本质的揭示、数学文化、数学教有技术、数学竞赛有 初步的了解
1.同一例题的不同命运 2.为什么扣两分? 3.荒唐的假设 4.i 的意义是什么? 第七章 数学教学设计 1.教学基本要求 领会数学教学设计的指导思想,编制数学教学目标的要求以及设计意图的形成工过程。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解教学设计、教案。教学目标的概念。 3.教学重点和难点 重点:数学教学设计意图的形成;难点:形成形成有创意的数学教学设计。 4.教学内容 第一节 教案三要素 1.教学设计及教案三要素 2.教学设计案例讲评 第二节 数学教学目标的确定 1.远期目标 2.近期目标 3.过程性目标 第三节 设计意图的形成 1.数学问题的教学设计 2.数学概念的教学设计 3.数学命题的教学设计 4.数学知识应用的教学设计 5.巩固课的教学设计 第四节 教学过程的展示 1.设计意图的形成 2.优秀创意设计举例 第八章 数学研究的一些特定课题 1.教学基本要求 对数学教育研究的特殊领域数学本质的揭示、数学文化、数学教育技术、数学竞赛有 初步的了解

2.要求学生掌握的基本概念、理论。 通过本章学习,使学生能够理解数学本质、数学文化、数学教有技术等概念 3.教学重点和难点 重点:数学本质的揭示 难点:数学本质的揭示。 4.教学内容 第一节数学教学本质的揭示 1.透过现象看本质 2.数学操作活动要体现本质 3.高屋建瓴地解释数学知识间的联系 第二节学习心理学与数学教育 1.行为主义心理学与数学教有 2.认知心理学与数学教有 第三节数学史与数学教育 1.数学史与数学教育作用 2.数学史教育的原则 第四节数学教育技术 1.数学教育技术 2.数学教有技术的应用 第五节数学优秀生的培养与数学竞赛 1.数学优秀生的培养方法 2.数学竞赛的作用 第九章数学问题与数学考试 1.教学基本要求 能对数学问题有与时俱进的理解,对数学问题解决有较深刻的认识。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解数学问题、问题解决教学的概念,掌握数学问题解决 教学的策略 3.教学重点和难点 重点:掌握一定的科学的问题解决策略。 难点:掌握一定的科学的问题解决策略 4.教学内容 第一节数学问题与数学解题
2.要求学生掌握的基本概念、理论。 通过本章学习,使学生能够理解数学本质、数学文化、数学教育技术等概念。 3.教学重点和难点 重点: 数学本质的揭示。 难点:数学本质的揭示。 4.教学内容 第一节 数学教学本质的揭示 1.透过现象看本质 2.数学操作活动要体现本质 3.高屋建瓴地解释数学知识间的联系 第二节 学习心理学与数学教育 1.行为主义心理学与数学教育 2.认知心理学与数学教育 第三节 数学史与数学教育 1.数学史与数学教育作用 2.数学史教育的原则 第四节 数学教育技术 1.数学教育技术 2.数学教育技术的应用 第五节 数学优秀生的培养与数学竞赛 1. 数学优秀生的培养方法 2. 数学竞赛的作用 第九章 数学问题与数学考试 1.教学基本要求 能对数学问题有与时俱进的理解,对数学问题解决有较深刻的认识。 2.要求学生掌握的基本概念、理论 通过本章学习,使学生能够理解数学问题、问题解决教学的概念,掌握数学问题解决 教学的策略 3.教学重点和难点 重点: 掌握一定的科学的问题解决策略。 难点:掌握一定的科学的问题解决策略。 4.教学内容 第一节 数学问题与数学解题

1.数学问题是什么 2.数学解题的过程和方法 第二节数学应用题、情境题、开放题 1.数学应用题类型及编制 2.情境类型及编制题 3.开放题的类型及编制 第三节问题解决的教学 1.间题解决教学的策略 2.数学问题的类型 第十章数学教育研究 1.教学基本要求 对数学教育研究地位、类型有全面的了解,对教有论文的习作有初步的了解,为数学 教育研究论文的写作做铺垫。 2要求学生掌握的基本概念、理论。 通过本章学习,使学生了解毕业论文写作的结构、过程和基本要求 3.教学重点和难点 重点:教有论文的写作要求。 难点:教有论文的写作。 4.教学内容 第一节数学教育研究的有关认识 1.数学教有研究的定位 2,数学教有研究的课颗类型 3.选择论题的策略 第二节优秀数学教育论文选读 1,阅读代表性的数学教育论文 第三节数学教育论文的习作 1.论文的基本结构 2.撰写论文的一般过程 3.毕业论文写作的基本要求 四、学时分配表
1.数学问题是什么 2.数学解题的过程和方法 第二节 数学应用题、情境题、开放题 1.数学应用题类型及编制 2.情境类型及编制题 3.开放题的类型及编制 第三节 问题解决的教学 1.问题解决教学的策略 2.数学问题的类型 第十章 数学教育研究 1.教学基本要求 对数学教育研究地位、类型有全面的了解,对教育论文的习作有初步的了解,为数学 教育研究论文的写作做铺垫。 2.要求学生掌握的基本概念、理论。 通过本章学习,使学生了解毕业论文写作的结构、过程和基本要求。 3.教学重点和难点 重点:教育论文的写作要求。 难点:教育论文的写作。 4.教学内容 第一节 数学教育研究的有关认识 1.数学教育研究的定位 2.数学教育研究的课题类型 3.选择论题的策略 第二节 优秀数学教育论文选读 1.阅读代表性的数学教育论文 第三节 数学教育论文的习作 1.论文的基本结构 2.撰写论文的一般过程 3.毕业论文写作的基本要求 四、学时分配表
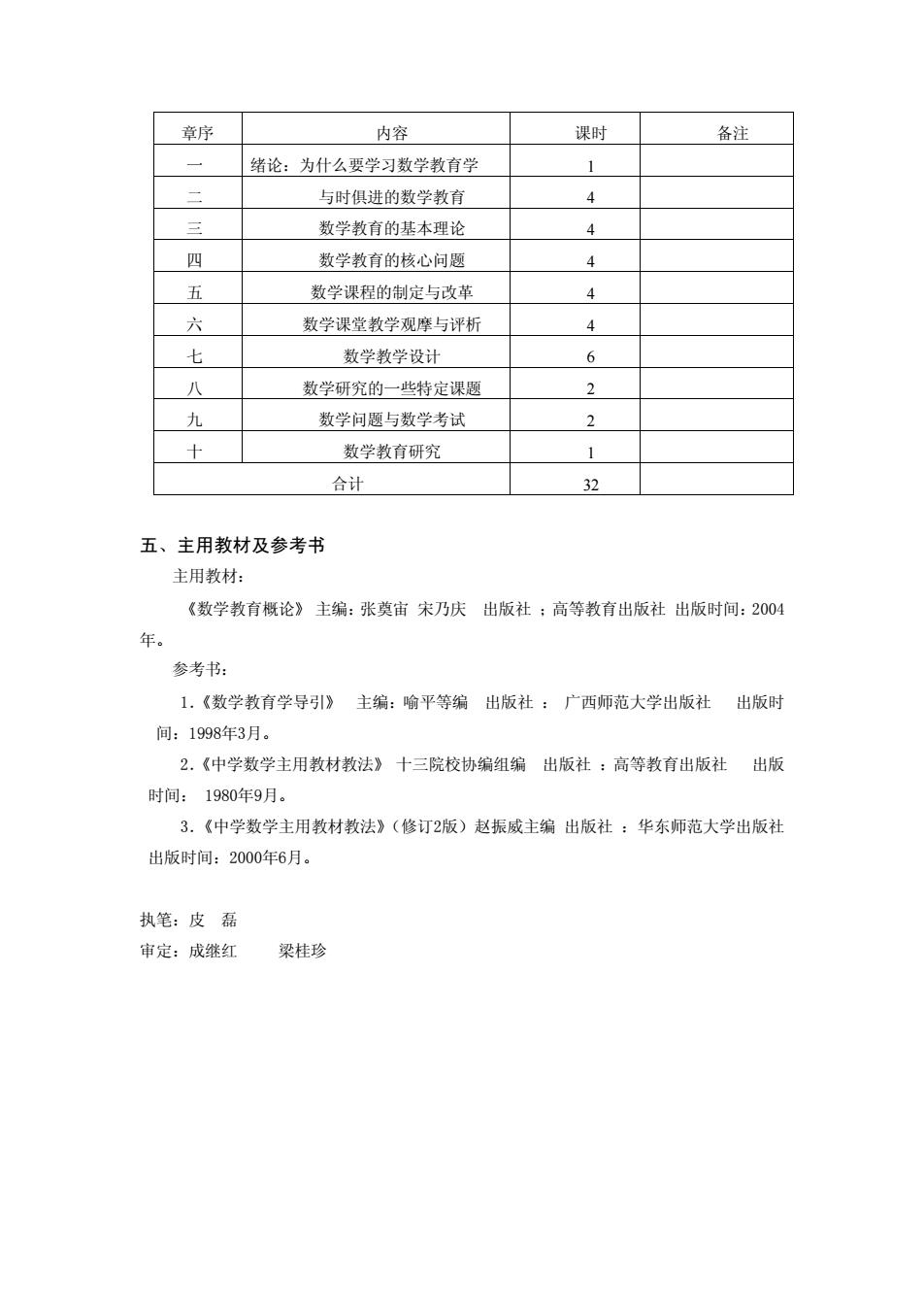
章序 内容 课时 备注 绪论:为什么要学习数学教有学 1 与时俱进的数学教有 4 数学教育的基本理论 4 四 数学教育的核心问题 4 数学课程的制定与改革 六 数学课堂教学观摩与评析 4 数学数学设计 6 数学研究的一些特定课题 2 九 数学问题与数学考试 2 数学教育研究 1 合计 32 五、主用教材及参考书 主用教材: 《数学教育概论》主编:张莫宙宋乃庆出版社:高等教育出版社出版时间:004 年。 参考书: 1.《数学教有学导引》主编:喻平等编出版社:广西师范大学出版社出版时 间:1998年3月。 2.《中学数学主用教材教法》十三院校协编组编出版社:高等教有出版社出版 时间:1980年9月。 3.《中学数学主用教材教法》(修订2版)赵振威主编出版社:华东师范大学出版社 出版时间:2000年6月。 执笔:皮磊 审定:成继红 梁桂珍
章序 内容 课时 备注 一 绪论:为什么要学习数学教育学 1 二 与时俱进的数学教育 4 三 数学教育的基本理论 4 四 数学教育的核心问题 4 五 数学课程的制定与改革 4 六 数学课堂教学观摩与评析 4 七 数学教学设计 6 八 数学研究的一些特定课题 2 九 数学问题与数学考试 2 十 数学教育研究 1 合计 32 五、主用教材及参考书 主用教材: 《数学教育概论》 主编:张奠宙 宋乃庆 出版社 ;高等教育出版社 出版时间:2004 年。 参考书: 1.《数学教育学导引》 主编:喻平等编 出版社 : 广西师范大学出版社 出版时 间:1998年3月。 2.《中学数学主用教材教法》 十三院校协编组编 出版社 :高等教育出版社 出版 时间: 1980年9月。 3.《中学数学主用教材教法》(修订2版)赵振威主编 出版社 :华东师范大学出版社 出版时间:2000年6月。 执笔:皮 磊 审定:成继红 梁桂珍