
《抽象代数》教学大纲 课程编码:1511101403 课程名称:抽象代数 学时/学分:48/3 先修课程:《高等代数》 适用专业:数学与应用数学 开课教研室:代数与几何教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的一门重要的专业选修课。 2.课程任务:使学生对抽象代数的思想和方法有较深刻的认识,提高抽象思维、逻辑 推理和运算的能力:使学生获得一定的抽象代数的基础知识,受到代数方法的初步训练,为 进一步学习代数后继课程打下基础:使学生能应用抽象代数的知识与方法去理解与处理有关 的问题,培养与提高学生应用抽象代数的理论分析问题与解决问题的能力。 二、课程教学基本要求 本课程讲授代数中典型的代数系统:群、环、域。要求学生能了解群的各种定义,循 环群,阶对称群,变换群,陪集,不变子群的定义及其性质,了解环、域、理想、唯一分 解的定义。能够计算群的元素阶,环中可逆元,零因子、素元,掌握Lagrange定理,群、 环同态和同构基本定理,堂挥判别唯一分解环的方法。堂挥扩域、单扩域、代数扩域、分裂 域、有限域的定义及性质。 成绩考核形式:末考成绩(闭卷考试)(70%)+平时成绩(平时测验、作业、课堂提问、 课堂讨论等)(30%)。成绩评定采用百分制,60分为及格。 三、课程教学内容 第一章群论 1.教学基本要求 让学生掌握群、子群、商群的定义及循环群、置换群、有限群的定义及性质,理解并学 握群的同态基本定理。 2.要求学生掌握的基本概念、理论、技能 通过本章教学使学生掌握有限群、无限群、群的阶和交换群的概念:理解群同构、同态 的定义,掌握群同态的有关性质:掌握循环群的定义和由生成元决定循环群的性质与特点: 熟练掌握剩余类加群,并能证明任一循环群可以与整数加群或模为的剩余类加群同构,以 及与循环群同态的群的性质:了解有限群的定义
《抽象代数》教学大纲 课程编码:1511101403 课程名称:抽象代数 学时/学分:48/3 先修课程:《高等代数》 适用专业:数学与应用数学 开课教研室:代数与几何教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的一门重要的专业选修课。 2.课程任务:使学生对抽象代数的思想和方法有较深刻的认识,提高抽象思维、逻辑 推理和运算的能力;使学生获得一定的抽象代数的基础知识,受到代数方法的初步训练,为 进一步学习代数后继课程打下基础;使学生能应用抽象代数的知识与方法去理解与处理有关 的问题,培养与提高学生应用抽象代数的理论分析问题与解决问题的能力。 二、课程教学基本要求 本课程讲授代数中典型的代数系统:群、环、域。要求学生能了解群的各种定义,循 环群,n 阶对称群,变换群,陪集,不变子群的定义及其性质,了解环、域、理想、唯一分 解的定义。能够计算群的元素阶,环中可逆元,零因子、素元,掌握 Lagrange 定理,群、 环同态和同构基本定理,掌握判别唯一分解环的方法。掌握扩域、单扩域、代数扩域、分裂 域、有限域的定义及性质。 成绩考核形式:末考成绩(闭卷考试)(70%)+平时成绩(平时测验、作业、课堂提问、 课堂讨论等)(30%)。成绩评定采用百分制,60 分为及格。 三、课程教学内容 第一章 群 论 1.教学基本要求 让学生掌握群、子群、商群的定义及循环群、置换群、有限群的定义及性质,理解并掌 握群的同态基本定理。 2.要求学生掌握的基本概念、理论、技能 通过本章教学使学生掌握有限群、无限群、群的阶和交换群的概念;理解群同构、同态 的定义,掌握群同态的有关性质;掌握循环群的定义和由生成元决定循环群的性质与特点; 熟练掌握剩余类加群,并能证明任一循环群可以与整数加群或模为 n 的剩余类加群同构,以 及与循环群同态的群的性质;了解有限群的定义

3.教学重点和难点 教学重点是群的定义、判定、性质:正规子群和商群的定义和性质:教学难点是群的 同态基本定理的证明和简单应用。 4.教学内容 第一节代数运算 1.代数运算的定义及表示法 2.结合律、交换律、清去律的定义 第二节 群的概念 1.群的定义及基本性质 2.单位元、逆元的概念 3.变换群、置换群的定义及性质 第三节 子群 1.子群的定义、性质 2.非空子集合构成子群的充要条件 3.生成子群、循环群的定义 4.元素的阶的概念,元素阶的几个性质定理 第四节 循环群 1.循环群的性质 2.有限循环群和无限循环群 第五节 正规子群与商群 1.暗集、指数的概念 2.正规子群的定义、判定定理 3.商群的定义、基本性质 4.模n的剩余类群 第六节群的同构与同态 1.群同构、同态的定义 2.群的同态基本定理及应用 ★第七节 有限群 1.Lagrange定理 2.Sy1ow定理 第二章环论 1.教学基本要求
3.教学重点和难点 教学重点是群的定义、判定、性质;正规子群和商群的定义和性质;教学难点是群的 同态基本定理的证明和简单应用。 4.教学内容 第一节 代数运算 1.代数运算的定义及表示法 2.结合律、交换律、消去律的定义 第二节 群的概念 1.群的定义及基本性质 2.单位元、逆元的概念 3.变换群、置换群的定义及性质 第三节 子 群 1.子群的定义、性质 2.非空子集合构成子群的充要条件 3.生成子群、循环群的定义 4.元素的阶的概念,元素阶的几个性质定理 第四节 循环群 1.循环群的性质 2.有限循环群和无限循环群 第五节 正规子群与商群 1.陪集、指数的概念 2.正规子群的定义、判定定理 3.商群的定义、基本性质 4.模 n 的剩余类群 第六节 群的同构与同态 1.群同构、同态的定义 2.群的同态基本定理及应用 ★第七节 有限群 1.Lagrange 定理 2.Sylow 定理 第二章 环 论 1.教学基本要求

掌握环、子环、理想、商环、整环的定义,理解并掌握环的同态基本定理,了解欧式 环、主理想整环、唯一分解整环的定义及性质。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生理解掌握加群的定义:熟悉环的定义,环中的计算规则:理解 交换环的定义:熟悉单位元、逆元和零因子的性质并能熟练运用:掌握消去律与零因子的关 系:了解除环的定义,能够举出域的例子:除环与加群、乘群的关系,理顺环一交换环、 有单位元的环和无零因子环一整环、除环 一域的关系。 3.教学重点和难点 教学重点是环、域、理想:教学难点是环的同态、极大理想、商环。 4.教学内容 第一节 环的概念 1.环的定义、例子 2.环的简单性质 第二节 多项式环 1.一元多项式环的定义 2.多元多项式环的定义 第三节 理想与商环 1.理想的定义、简单性质及判定定理 2.生成理想、主理想的定义 3.商环的定义、性质 4.模n的剩余类环 第四节 环的同态 1.环同态、同构的定义 2.环的同态基本定理 3.挖补定理 第五节 交换环 1.素理想的定义及性质 2.极大理想的定义及性质 3.素理想和极大理想的关系 4.整环的特征 5.商域的构造 第六节 整环的因子分解 1.素理想的定义及性质 2.极大理想的定义及性质
掌握环、子环、理想、商环、整环的定义,理解并掌握环的同态基本定理,了解欧式 环、主理想整环、唯一分解整环的定义及性质。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生理解掌握加群的定义;熟悉环的定义,环中的计算规则;理解 交换环的定义;熟悉单位元、逆元和零因子的性质并能熟练运用;掌握消去律与零因子的关 系;了解除环的定义,能够举出域的例子;除环与加群、乘群的关系,理顺环——交换环、 有单位元的环和无零因子环——整环、除环——域的关系。 3.教学重点和难点 教学重点是环、域、理想;教学难点是环的同态、极大理想、商环。 4.教学内容 第一节 环的概念 1.环的定义、例子 2.环的简单性质 第二节 多项式环 1.一元多项式环的定义 2.多元多项式环的定义 第三节 理想与商环 1.理想的定义、简单性质及判定定理 2.生成理想、主理想的定义 3.商环的定义、性质 4.模 n 的剩余类环 第四节 环的同态 1.环同态、同构的定义 2.环的同态基本定理 3.挖补定理 第五节 交换环 1.素理想的定义及性质 2.极大理想的定义及性质 3.素理想和极大理想的关系 4.整环的特征 5.商域的构造 第六节 整环的因子分解 1.素理想的定义及性质 2.极大理想的定义及性质

3.素理想和极大理想的关系 4.整环的特征 5.商域的构造 第三章域论 1.教学基本要求 掌握子域、扩域的定义:理解并掌握单扩域、代数扩域、超越扩域、分裂域的定义及 性质。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生了解域论的基本概念:掌握单扩域、代数扩域、超越扩域、分裂 域、有限域的定义、结构、存在性、唯一性等基本性质。 3.教学重点和难点 教学重点是扩域、素域、代数扩域、超越扩域:教学难点是代数扩域、超越扩域。 4.教学内容 第一节子域和扩域 1.子域、扩域的定义 2.有限扩域的定义 3.有限扩域的性质 第二节单扩城 1.单扩域的结构定理 2.单代数扩域、单超越扩域的定义 3.极小多项式的定义 4.极小多项式的性质 第三节代数扩域 1.代数扩域、超越扩域的定义 2.代数扩域的性质 第四节 分裂域 1.分裂域的定义 2.分裂域的存在性和唯一性 ★第五节 有限域 1.有限域的定义 2.有限域的存在性和唯一性 3.有限域的子域 说明:带★的内容为选讲内容
3.素理想和极大理想的关系 4.整环的特征 5.商域的构造 第三章 域 论 1.教学基本要求 掌握子域、扩域的定义;理解并掌握单扩域、代数扩域、超越扩域、分裂域的定义及 性质。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生了解域论的基本概念;掌握单扩域、代数扩域、超越扩域、分裂 域、有限域的定义、结构、存在性、唯一性等基本性质。 3.教学重点和难点 教学重点是扩域、素域、代数扩域、超越扩域;教学难点是代数扩域、超越扩域。 4.教学内容 第一节 子域和扩域 1.子域、扩域的定义 2.有限扩域的定义 3.有限扩域的性质 第二节 单扩域 1.单扩域的结构定理 2.单代数扩域、单超越扩域的定义 3.极小多项式的定义 4.极小多项式的性质 第三节 代数扩域 1.代数扩域、超越扩域的定义 2.代数扩域的性质 第四节 分裂域 1.分裂域的定义 2.分裂域的存在性和唯一性 ★第五节 有限域 1.有限域的定义 2.有限域的存在性和唯一性 3.有限域的子域 说明:带★的内容为选讲内容
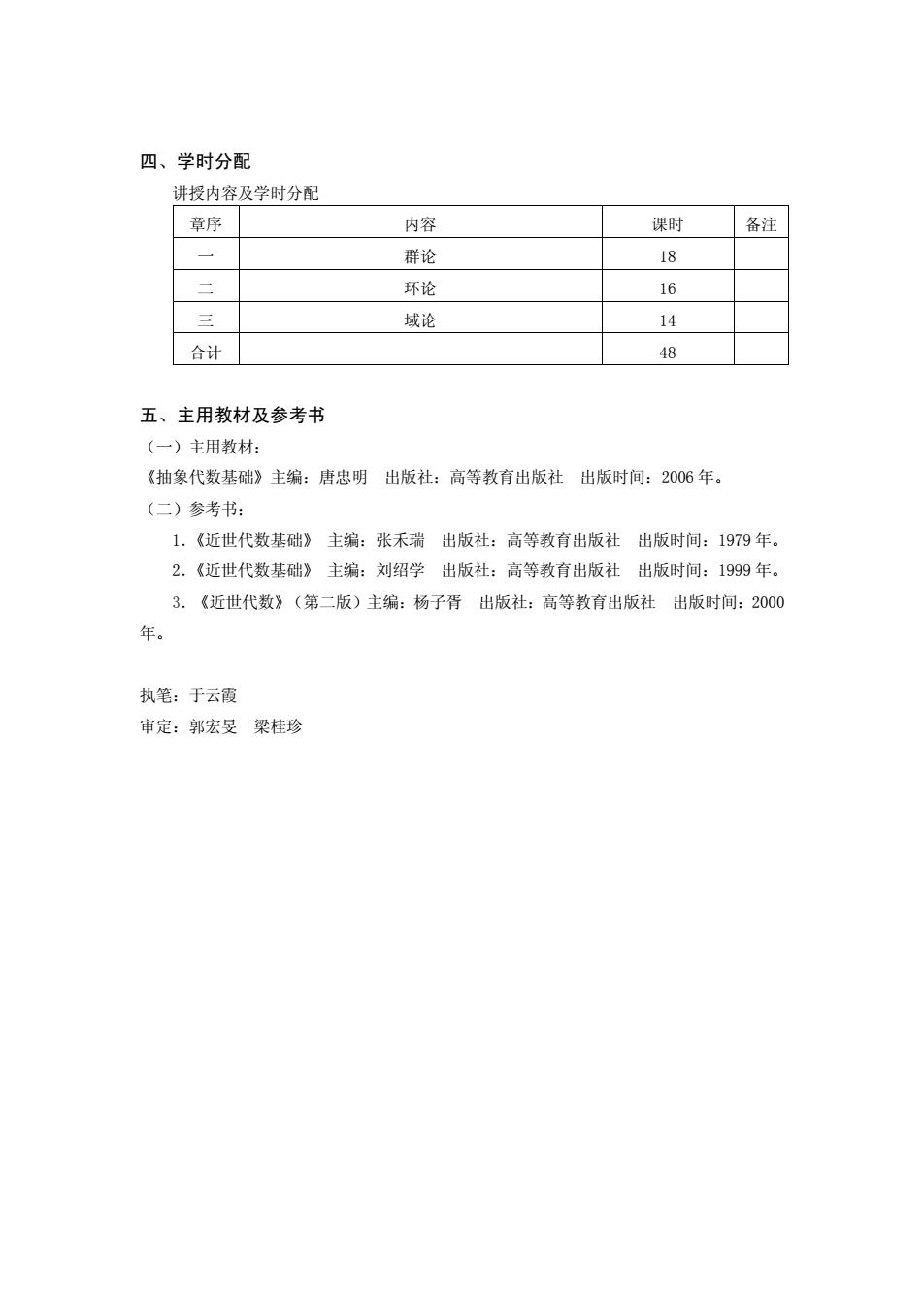
四、学时分配 讲授内容及学时分配 章序 内容 课时 名注 群论 18 环论 16 域论 14 合计 48 五、主用教材及参考书 (一)主用教材: 《抽象代数基础》主编:唐忠明出版社:高等教有出版社出版时间:2006年。 (二)参考书: 1.《近世代数基础》主编:张禾瑞出版社:高等教育出版社出版时间:1979年 2.《近世代数基础》主编:刘绍学出版社:高等教育出版社出版时间:1999年。 3.《近世代数》(第二版)主编:杨子背出版社:高等教育出版社出版时间:2000 年。 执笔:于云霞 审定:郭宏旻梁桂珍
四、学时分配 讲授内容及学时分配 章序 内容 课时 备注 一 群论 18 二 环论 16 三 域论 14 合计 48 五、主用教材及参考书 (一)主用教材: 《抽象代数基础》主编:唐忠明 出版社:高等教育出版社 出版时间:2006 年。 (二)参考书: 1.《近世代数基础》 主编:张禾瑞 出版社:高等教育出版社 出版时间:1979 年。 2.《近世代数基础》 主编:刘绍学 出版社:高等教育出版社 出版时间:1999 年。 3.《近世代数》(第二版)主编:杨子胥 出版社:高等教育出版社 出版时间:2000 年。 执笔:于云霞 审定:郭宏旻 梁桂珍