
《数学分析V》教学大纲 课程编码:1511100403 课程名称:数学分析 学时/学分:54/3 先修课程:《初等数学》、《数学分析I》、《数学分析II》、《数学分析III》 适用专业:数学与应用数学专业 开课教研室:分析与方程教研室 一、课程性质与任务 1.课程性质:《数学分析Ⅳ》是数学与应用数学专业的一门重要的核心课程,它的主要 内容为多元函数积分理论。它是进行数学研究的理论基础,着重研究解决数学问题的基础 方法及其理论. 2.课程任务:开设本课程的目的是培养学生具有抽象思维能力、逻辑推理能力、空间 想象能力、运算能力和综合运用所学的知识分析和解决问题的能力。通过系统的学习与严格 的训练,使学生全面掌握数学分析中的多元函数积分理论:提高建立数学模型并应用多元函 数积分理论工具解决实际应用问题的能力。 二、课程教学基本要求 1.掌握含参量正常积分及性质:掌握对含参量积分的求导方法:掌握含参量非正常积 分及性质、一致收敛判别法:掌捏下函数与B函数的定义与性质。 2.深刻理解第一型、第二型曲线积分,第一型、第二型曲线积分的概念及物理意义:掌 握第一型、第二型曲线积分的计算;掌握第一型、第二型曲线积分联系 3.掌握平面有界点集可求面积的条件:掌握二重积分可积性判定:深刻理解二重积分 三重积分的概念及二重积分的几何意义:了解二重积分存在的条件及重积分的性质:熟练掌 握化二重积分、三重积分为累次积分的方法:掌握重积分的换元法。牢固掌握二重积分变 量变换定理:掌握利用重积分计算曲面面积的方法,了解重积分在物理中的应用:了解重 积分:了解反常二重积分。 4.理解简单闭曲线,域的连通性,曲面的侧等概念:牢固掌握高斯公式、斯托克斯公式: 了解两类曲面积分,两类曲面积分的联系:熟练掌握曲面积分,曲面积分的计算。 5.了解更一般形式的多元函数理论:深化经典导数的概念:了解更一般形式的反函数 定理和隐函数定理:了解外积、微分形式与一般斯托克斯公式。 本课程的成绩考核形式:末考成绩(闭卷考试)(70%)十平时成绩(平时测验、作业 课堂提问、课堂讨论等)(30%)。成绩评定采用百分制,60分为及格
《数学分析Ⅳ》教学大纲 课程编码:1511100403 课程名称:数学分析 学时/学分:54/3 先修课程:《初等数学》、《数学分析 I》、《数学分析 II》、《数学分析 III》 适用专业:数学与应用数学专业 开课教研室:分析与方程教研室 一、课程性质与任务 1.课程性质:《数学分析Ⅳ》是数学与应用数学专业的一门重要的核心课程,它的主要 内容为多元函数积分理论。 它是进行数学研究的理论基础,着重研究解决数学问题的基础 方法及其理论. 2.课程任务:开设本课程的目的是培养学生具有抽象思维能力、逻辑推理能力、空间 想象能力、运算能力和综合运用所学的知识分析和解决问题的能力。通过系统的学习与严格 的训练,使学生全面掌握数学分析中的多元函数积分理论;提高建立数学模型并应用多元函 数积分理论工具解决实际应用问题的能力。 二、课程教学基本要求 1.掌握含参量正常积分及性质;掌握对含参量积分的求导方法;掌握含参量非正常积 分及性质、一致收敛判别法;掌握 Γ 函数与 β 函数的定义与性质。 2.深刻理解第一型、第二型曲线积分,第一型、第二型曲线积分的概念及物理意义;掌 握第一型、第二型曲线积分的计算;掌握第一型、第二型曲线积分联系。 3.掌握平面有界点集可求面积的条件;掌握二重积分可积性判定;深刻理解二重积分、 三重积分的概念及二重积分的几何意义;了解二重积分存在的条件及重积分的性质;熟练掌 握化二重积分、三重积分为累次积分的方法;掌握重积分的换元法. 牢固掌握二重积分变 量变换定理;掌握利用重积分计算曲面面积的方法,了解重积分在物理中的应用;了解 n 重 积分;了解反常二重积分。 4.理解简单闭曲线,域的连通性,曲面的侧等概念;牢固掌握高斯公式、斯托克斯公式; 了解两类曲面积分,两类曲面积分的联系;熟练掌握曲面积分,曲面积分的计算。 5.了解更一般形式的多元函数理论;深化经典导数的概念;了解更一般形式的反函数 定理和隐函数定理;了解外积、微分形式与一般斯托克斯公式。 本课程的成绩考核形式:末考成绩(闭卷考试)(70%)+平时成绩(平时测验、作业、 课堂提问、课堂讨论等)(30%)。成绩评定采用百分制,60 分为及格

三、课程教学内容 第十九章含参量积分 1.教学基本要求 (1)学握含参量正常积分及性质,掌握对含参量积分的求导方法。 (2)掌握含参量反常积分及性质、一致收敛判别法。 (3)掌握下函数与B函数的定义与性质。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握含参量积分的定义、下函数与B函数的定义。掌握含参量 反常积分一致收敛判别法,掌握下函数与B函数的性质。掌握对含参量积分的求导方法。 3.教学重点和难点 教学重点是系统讨论含参变量的反常积分的一致收敛的判别法及一致收敛积分的分析 性质,掌握Beta函数和Gamma函数的性质、递推公式及二者之间的关系。教学难点是含 参变量的反常积分一致收敛的判别法及一致收敛积分的分析性质:用含参变量积分的分析性 质计算定积分,参变量的反常积分计算反常积分。 4.教学内容 第一节 含参量正常积分 1.含参量正常积分的定义 2.含参量正常积分的分析性质 第二节 含参量反常积分 1.一致收敛性及判别法 2.含参量反常积分的性质 第三节 歌拉积分 1.下函数 2.B函数 3.下函数与B函数之间的关系 第二十章曲线积分 1.教学基本要求 (1)深刻理解第一型、第二型曲线积分的概念及物理意义。 (2)掌握第一型、第二型曲线积分的计算。 (3)掌握第一型、第二型曲线积分联系。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握第一型、第二型曲线积分的概念,掌握第一型、第二型曲线
三、课程教学内容 第十九章 含参量积分 1.教学基本要求 (1)掌握含参量正常积分及性质,掌握对含参量积分的求导方法。 (2)掌握含参量反常积分及性质、一致收敛判别法。 (3)掌握 Γ 函数与 β 函数的定义与性质。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握含参量积分的定义、Γ 函数与 β 函数的定义。掌握含参量 反常积分一致收敛判别法,掌握 Γ 函数与 β 函数的性质。掌握对含参量积分的求导方法。 3.教学重点和难点 教学重点是系统讨论含参变量的反常积分的一致收敛的判别法及一致收敛积分的分析 性质,掌握 Beta 函数和 Gamma 函数的性质、递推公式及二者之间的关系。教学难点是含 参变量的反常积分一致收敛的判别法及一致收敛积分的分析性质;用含参变量积分的分析性 质计算定积分,参变量的反常积分计算反常积分。 4.教学内容 第一节 含参量正常积分 1.含参量正常积分的定义 2.含参量正常积分的分析性质 第二节 含参量反常积分 1.一致收敛性及判别法 2.含参量反常积分的性质 第三节 欧拉积分 1.Γ函数 2.B 函数 3.Γ函数与 B 函数之间的关系 第二十章 曲线积分 1.教学基本要求 (1)深刻理解第一型、第二型曲线积分的概念及物理意义。 (2)掌握第一型、第二型曲线积分的计算。 (3)掌握第一型、第二型曲线积分联系。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握第一型、第二型曲线积分的概念,掌握第一型、第二型曲线

积分的计算。 3.教学重点和难点 教学重点是第一型、第二型曲线积分的概念及物理意义,第一型、第二型曲线积分的计 算。教学难点是两类曲线积分的联系。 4.教学内容 第一节 第一型曲线积分 1.第一型曲线积分的定义 2.第一型曲线积分的计算 第二节 第二型曲线积分 1.第二型曲线积分的定义 2.第二型曲线积分的计算 3.两类曲线积分的联系 第二十一章重积分 1.教学基本要求 (1)掌握平面有界点集可求面积的条件。 (2)掌握二重积分可积性判定。 (3)深刻理解二重积分、三重积分的概念及二重积分的几何意义。 (4)了解二重积分存在的条件及重积分的性质。 (5)熟练掌握化二重积分、三重积分为累次积分的方法。 (6)掌握重积分的换元法.牢固掌握二重积分变量变换定理。 (7)掌握利用重积分计算曲面面积的方法,了解重积分在物理中的应用 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握二重积分、三重积分的概念。掌握二重积分可积性判定。掌 握重积分的换元法。牢固掌握二重积分变量变换定理。熟练掌握化二重积分、三重积分为 累次积分的方法。掌握利用重积分计算曲面面积的方法。 3.教学重点和难点 教学重点是重积分的概念:格林公式:曲线积分与路线无关的四个等价条件;二重积分 与三重积分算法:二重积分与三重积分的变量代换:重积分的应用。教学难点是二重积分的 变量变换定理。 4.教学内容 第一节 二重积分的概念 1.平面图形的面积 2.二重积分的定义及其存在性
积分的计算。 3.教学重点和难点 教学重点是第一型、第二型曲线积分的概念及物理意义,第一型、第二型曲线积分的计 算。教学难点是两类曲线积分的联系。 4.教学内容 第一节 第一型曲线积分 1.第一型曲线积分的定义 2.第一型曲线积分的计算 第二节 第二型曲线积分 1.第二型曲线积分的定义 2.第二型曲线积分的计算 3.两类曲线积分的联系 第二十一章 重积分 1.教学基本要求 (1)掌握平面有界点集可求面积的条件。 (2)掌握二重积分可积性判定。 (3)深刻理解二重积分、三重积分的概念及二重积分的几何意义。 (4)了解二重积分存在的条件及重积分的性质。 (5) 熟练掌握化二重积分、三重积分为累次积分的方法。 (6) 掌握重积分的换元法. 牢固掌握二重积分变量变换定理。 (7) 掌握利用重积分计算曲面面积的方法,了解重积分在物理中的应用。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握二重积分、三重积分的概念。掌握二重积分可积性判定。掌 握重积分的换元法. 牢固掌握二重积分变量变换定理。 熟练掌握化二重积分、三重积分为 累次积分的方法。 掌握利用重积分计算曲面面积的方法。 3.教学重点和难点 教学重点是重积分的概念;格林公式;曲线积分与路线无关的四个等价条件;二重积分 与三重积分算法;二重积分与三重积分的变量代换;重积分的应用。教学难点是二重积分的 变量变换定理。 4.教学内容 第一节 二重积分的概念 1.平面图形的面积 2.二重积分的定义及其存在性

3.二重积分的性质 第二节 直角坐标系下二重积分的计算 1.化二重积分为累次积分的的计算公式 2.二重积分的计算 第三节 格林公式·曲线积分与路线的无关性 1,格林公式 2.曲线积分与路线的无关性 第四节 二重积分的的变量变换 1.二重积分的变量变换公式 2.用极坐标计算二重积分 第五节 三重积分 1.三重积分的概念 2.化三重积分为累次积分 3。三重积分换元法 第六节 重积分的应用 1,曲面面积 2.质心 3.转动惯量 4.引力 第二十二章曲面积分 1.教学基本要求 (1)理解简单闭曲线,域的连通性,曲面的侧等概念 (2)牢固掌握高斯公式、斯托克斯公式。 (3)了解两类曲面积分的联系。 (4)熟练掌握曲面积分的计算。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握简单闭曲线,域的连通性,曲面的侧等概念。掌握高斯公式 斯托克斯公式。掌握曲面积分的计算。 3.教学重点和难点 教学重点是曲面积分的概念,曲面积分的计算方法,Gauss公式和Stokes公式计算曲 面积分的方法。教学难点是两类曲面积分的联系,Gauss公式和Stokes公式计算曲面积分。 4.教学内容
3.二重积分的性质 第二节 直角坐标系下二重积分的计算 1.化二重积分为累次积分的的计算公式 2.二重积分的计算 第三节 格林公式·曲线积分与路线的无关性 1.格林公式 2.曲线积分与路线的无关性 第四节 二重积分的的变量变换 1.二重积分的变量变换公式 2.用极坐标计算二重积分 第五节 三重积分 1.三重积分的概念 2.化三重积分为累次积分 3.三重积分换元法 第六节 重积分的应用 1.曲面面积 2.质心 3.转动惯量 4.引力 第二十二章 曲面积分 1.教学基本要求 (1)理解简单闭曲线,域的连通性,曲面的侧等概念。 (2)牢固掌握高斯公式、斯托克斯公式。 (3)了解两类曲面积分的联系。 (4)熟练掌握曲面积分的计算。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生掌握简单闭曲线,域的连通性,曲面的侧等概念。掌握高斯公式、 斯托克斯公式。掌握曲面积分的计算。 3.教学重点和难点 教学重点是曲面积分的概念,曲面积分的计算方法,Gauss 公式和 Stokes 公式计算曲 面积分的方法。教学难点是两类曲面积分的联系,Gauss 公式和 Stokes 公式计算曲面积分。 4.教学内容
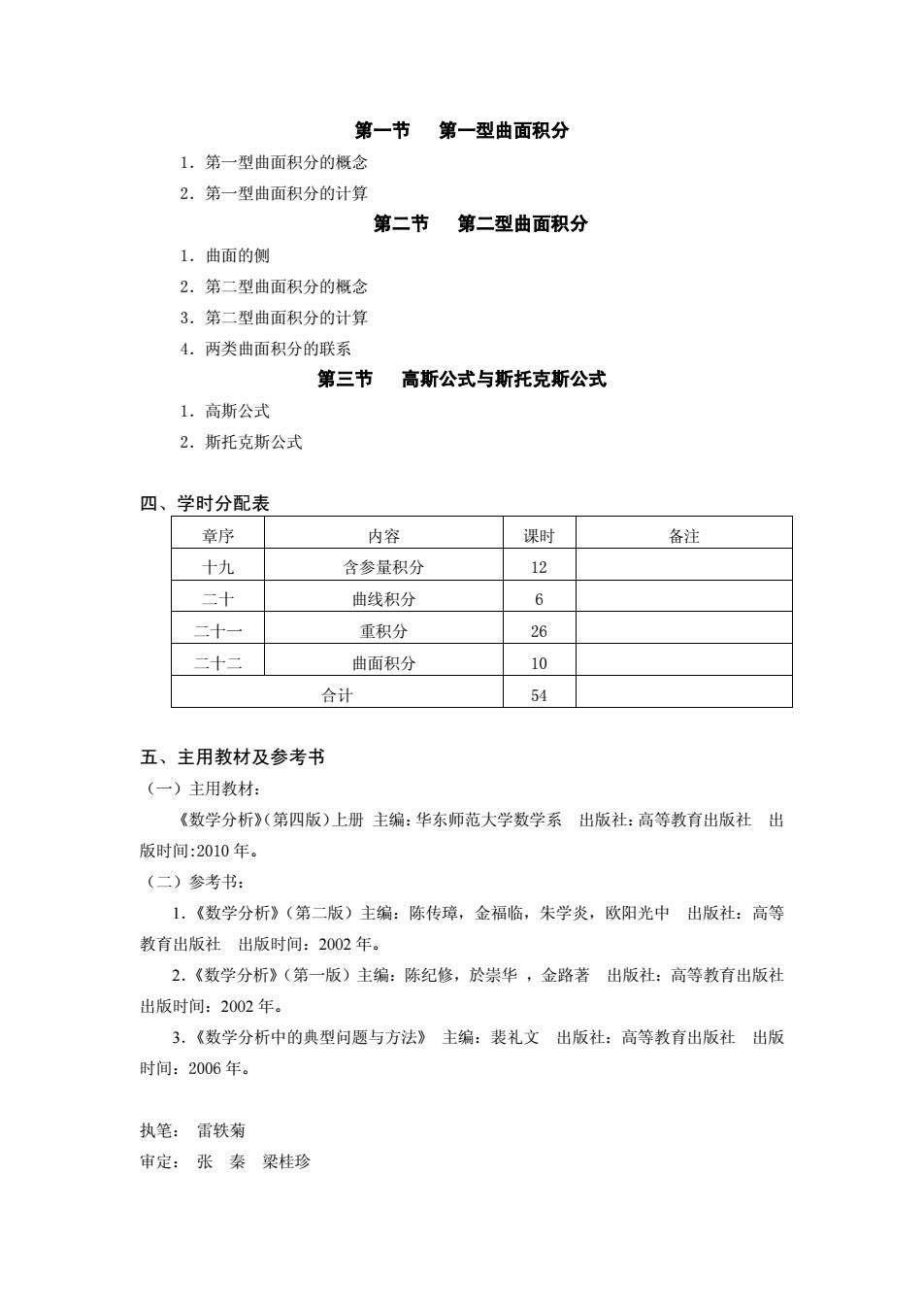
第一节第一型曲面积分 1.第一型曲面积分的概念 2.第一型曲面积分的计算 第二节第二型曲面积分 1.曲面的侧 2.第二型曲面积分的概念 3.第二型曲面积分的计算 4.两类曲面积分的联系 第三节 高斯公式与斯托克斯公式 1.高斯公式 2.斯托克斯公式 四、学时分配表 章序 内容 课时 各注 十九 含参量积分 12 二十 曲线积分 6 重积分 26 二十二 曲面积分 10 合计 54 五、主用教材及参考书 (一)主用教材: 《数学分析》(第四版)上册主编:华东师范大学数学系出版社:高等教育出版社出 版时间:2010年。 (二)参考书: 1.《数学分析》(第二版)主编:陈传璋,金福临,朱学炎,欧阳光中出版社:高等 教有出版社出版时间:2002年。 2.《数学分析》(第一版)主编:陈纪修,於崇华,金路著出版社:高等教有出版社 出版时间:2002年。 3.《数学分析中的典型问题与方法》主编:裴礼文出版社:高等教有出版社出版 时间:2006年。 执笔:雷轶菊 审定:张秦梁桂珍
第一节 第一型曲面积分 1.第一型曲面积分的概念 2.第一型曲面积分的计算 第二节 第二型曲面积分 1.曲面的侧 2.第二型曲面积分的概念 3.第二型曲面积分的计算 4.两类曲面积分的联系 第三节 高斯公式与斯托克斯公式 1.高斯公式 2.斯托克斯公式 四、学时分配表 章序 内容 课时 备注 十九 含参量积分 12 二十 曲线积分 6 二十一 重积分 26 二十二 曲面积分 10 合计 54 五、主用教材及参考书 (一)主用教材: 《数学分析》(第四版)上册 主编:华东师范大学数学系 出版社:高等教育出版社 出 版时间:2010 年。 (二)参考书: 1.《数学分析》(第二版)主编:陈传璋,金福临,朱学炎,欧阳光中 出版社:高等 教育出版社 出版时间:2002 年。 2.《数学分析》(第一版)主编:陈纪修,於崇华 ,金路著 出版社:高等教育出版社 出版时间:2002 年。 3.《数学分析中的典型问题与方法》 主编:裴礼文 出版社:高等教育出版社 出版 时间:2006 年。 执笔: 雷轶菊 审定: 张 秦 梁桂珍