
a 第2章关系数据库 新疆大学 软件学院
新疆大学 软件学院 第 2 章 关系数据库

2.1关系模型的数据结构及其形式化定义 2.2关系的码与关系的完整性 2.3关系代数 2.4关系演算* 2.5小、结
2.1 关系模型的数据结构及其形式化定义 2.2 关系的码与关系的完整性 2.3 关 系 代 数 2.4 关 系 演 算* 2.5 小 结

2.1关系模型的数据结构及其形式化定义 2.1.1关系的形式化定义及其有关概念 域Domain) 整数、实数和字符串的集合都是域 域是一组具有相同数据类型的值的集合,又称为值域 域中所包含的值的个数称为域的基数(用表示)。例如 →域名 ={李力,王平,刘伟},m1=3 D2{男,女};m2=2; P18,20,18}:m3=3
D1={李力,王平,刘伟},m1=3; D2={男,女};m2=2; D3={18,20,18};m3=3。 域是一组具有相同数据类型的值的集合,又称为值域 2.1 关系模型的数据结构及其形式化定义 2.1.1 关系的形式化定义及其有关概念 域(Domain) 整数、实数和字符串的集合都是域 域名 域中所包含的值的个数称为域的基数(用m表示)。例如 :

2.1关系模型的数据结构及其形式化定义 笛卡尔积(Cartesian Product) 给定一组域D,D2,.,D(它们可以包含相同的元素,即可以 完全不同,也可以部分或全部相同)。D,D2,.,D的笛卡尔积为 D1XD2X.X Dn={(d1,d2,.dn)dieDi,i=1,2,.n} 每一个元素(d1,d2,dn)中的每一个值di叫做一个分量(Component),di∈Di 每一个元素(d1,d2,dn)叫做一个n元组(n-Tuple),简称元组(Tuple)
D1×D2×.×Dn={(d1,d2,.,dn)|di∈Di,i=1,2,.,n} 每一个元素(d1,d2,.,dn)中的每一个值di叫做一个分量(Component),di∈Di 每一个元素(d1,d2,.,dn)叫做一个n元组(n-Tuple),简称元组(Tuple) 2.1 关系模型的数据结构及其形式化定义 给定一组域D1,D2,.,Dn(它们可以包含相同的元素,即可以 完全不同,也可以部分或全部相同)。D1,D2,.,Dn的笛卡尔积为 笛卡尔积(Cartesian Product)

2.1关系模型的数据结构及其形式化定义 笛卡尔积D1×D2×.×Dn的基数M(即元素(d1,d2,.,dn)的个数) 为所有域的基数的累乘之积,即M=m,· 例如,上述表示教师关系中姓名、性别两个域的笛卡尔积为: D1×D2={(李力,男),(李力,女),(王平,男), (王平,女),(刘伟,男),(刘伟,女)} 分量:李力、王平、刘伟、男、女 元组:(李力,男),(李力,女),M=m1×m2=3×2=6
2.1 关系模型的数据结构及其形式化定义 分量:李力、王平、刘伟、男、女 元组 :(李力,男),(李力,女) ,M=m1×m2=3×2=6 笛卡尔积D1×D2×.×Dn的基数M(即元素(d1,d2,.,dn)的个数) 为所有域的基数的累乘之积,即M= 。 例如,上述表示教师关系中姓名、性别两个域的笛卡尔积为: D1×D2={(李力,男),(李力,女),(王平,男), (王平,女),(刘伟,男),(刘伟,女)} = n i mi 1
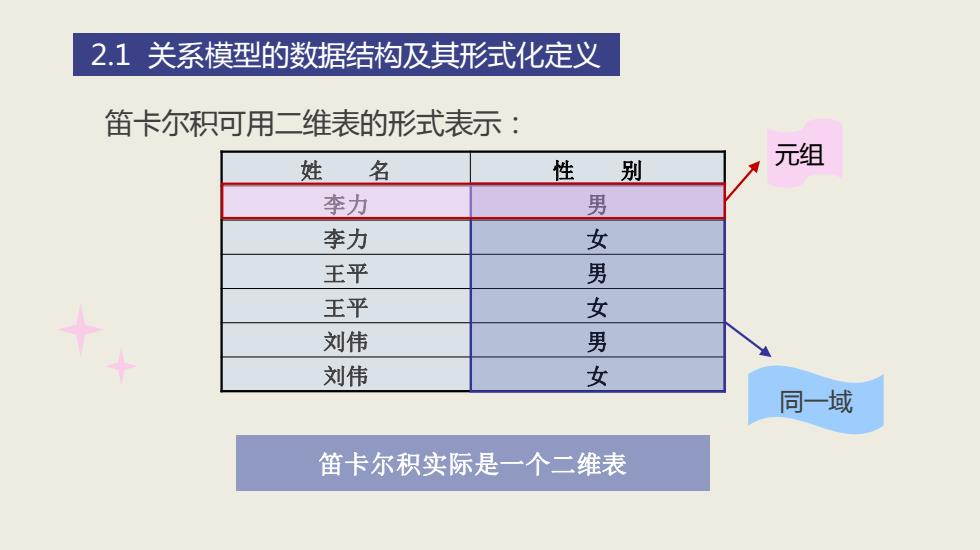
2.1关系模型的数据结构及其形式化定义 笛卡尔积可用二维表的形式表示: 姓 名 性 别 元组 李力 男 李力 女 王平 男 王平 女 刘伟 男 刘伟 女 同一域 笛卡尔积实际是一个二维表
姓 名 性 别 李力 男 李力 女 王平 男 王平 女 刘伟 男 刘伟 女 笛卡尔积实际是一个二维表 元组 同一域 2.1 关系模型的数据结构及其形式化定义 笛卡尔积可用二维表的形式表示:

2.1关系模型的数据结构及其形式化定义 第2章 关系(Relation) 笛卡尔积D×D2×.×D的任一子集称为定义在域D,D2,·,Dn上的n元关系(Relation) 关系的名字 n是关系的目或度 R (D1,D2.,Dn) D1XD2笛卡尔积的子集(关系T1) 如,上例D1×D2笛卡尔积的某个子集 姓名 性 别 可以构成教师关系1,如表2.2所示 李力 男引 王平 女 刘伟 男
2.1 关系模型的数据结构及其形式化定义 第2章 R(D1,D2.,Dn) 笛卡尔积D1×D2×.×Dn的任一子集称为定义在域D1,D2,.,Dn上的n元关系(Relation) 关系的名字 n是关系的目或度 姓 名 性 别 李力 男 王平 女 刘伟 男 如,上例D1×D2笛卡尔积的某个子集 可以构成教师关系T1,如表2.2所示 D1×D2笛卡尔积的子集(关系T1) 关系(Relation)
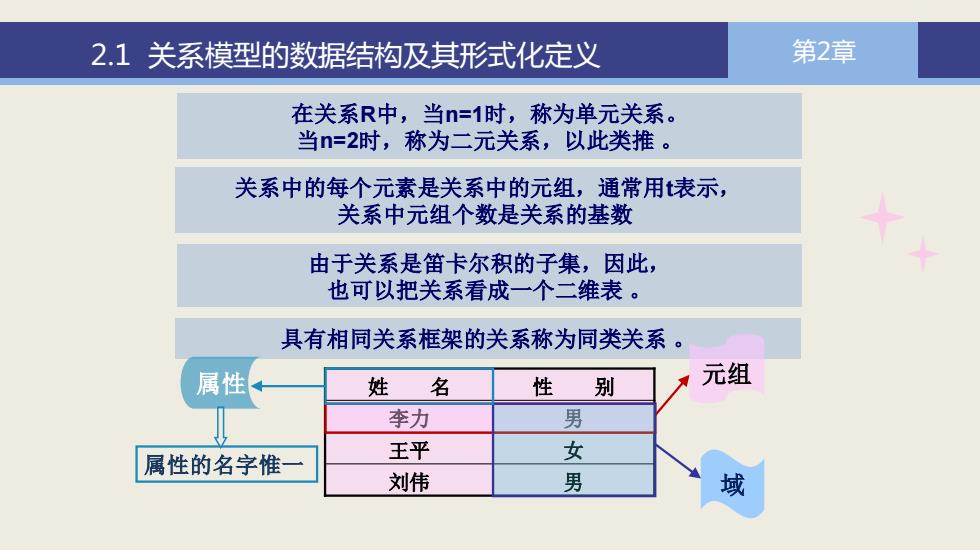
2.1关系模型的数据结构及其形式化定义 第2章 在关系R中,当n=1时,称为单元关系。 当n=2时,称为二元关系,以此类推。 关系中的每个元素是关系中的元组,通常用表示, 关系中元组个数是关系的基数 由于关系是笛卡尔积的子集,因此, 也可以把关系看成一个二维表。 具有相同关系框架的关系称为同类关系。 属性 姓 名 性 别 元组 李力 男 属性的名字惟一 王平 女 刘伟 男 域
2.1 关系模型的数据结构及其形式化定义 第2章 在关系R中,当n=1时,称为单元关系。 当n=2时,称为二元关系,以此类推 。 关系中的每个元素是关系中的元组,通常用t表示, 关系中元组个数是关系的基数 由于关系是笛卡尔积的子集,因此, 也可以把关系看成一个二维表 。 具有相同关系框架的关系称为同类关系 。 姓 名 性 别 李力 男 王平 女 刘伟 男 元组 域 属性 属性的名字惟一
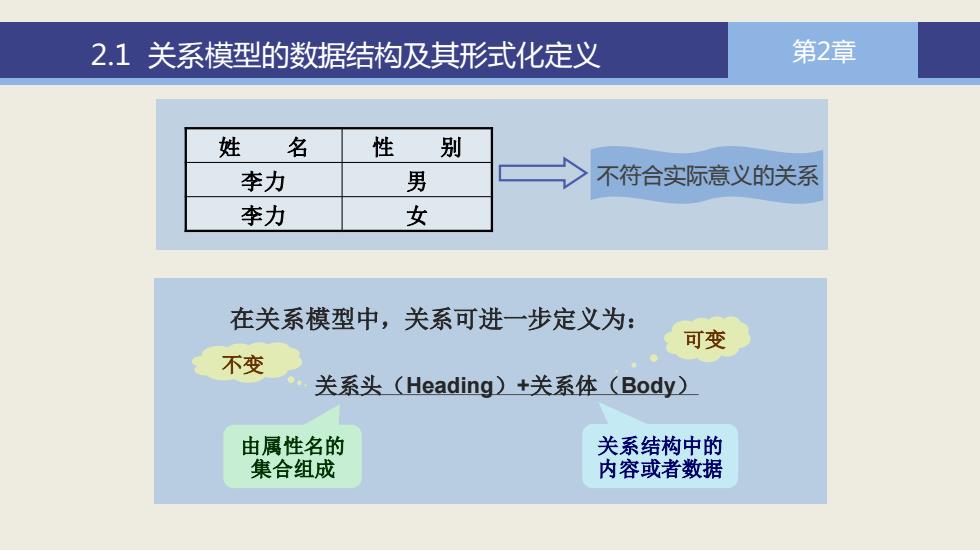
2.1关系模型的数据结构及其形式化定义 第2章 姓名 性别 李力 男 不符合实际意义的关系 李力 女 在关系模型中,关系可进一步定义为: 可变 不变 关系头(Heading)+关系体(Body) 由属性名的 关系结构中的 集合组成 内容或者数据
2.1 关系模型的数据结构及其形式化定义 第2章 姓 名 性 别 李力 男 李力 女 不符合实际意义的关系 由属性名的 集合组成 关系结构中的 内容或者数据 不变 可变 在关系模型中,关系可进一步定义为: 关系头(Heading)+关系体(Body)

2.1关系模型的数据结构及其形式化定义 第2章 2.1.2关系的性质 关系是一种规范化了的二维表中行的集合 每一列中的分量必须来自同一个域,必须是同一类型的数据。 ·不同的属性可来自同一个域,不同的属性必须有不同的名字。 ·列的顺序可以任意交换。 ·关系中元组的顺序(即行序)可任意。 ·关系中不允许出现相同的元组。 ·关系中每一分量必须是不可分的数据项
2.1 关系模型的数据结构及其形式化定义 第2章 2.1.2 关系的性质 关系是一种规范化了的二维表中行的集合 · 每一列中的分量必须来自同一个域,必须是同一类型的数据。 · 不同的属性可来自同一个域,不同的属性必须有不同的名字。 · 列的顺序可以任意交换。 · 关系中元组的顺序(即行序)可任意。 · 关系中不允许出现相同的元组。 · 关系中每一分量必须是不可分的数据项