
第四章分布式路由算法 分布式路由算法导论 ● 一般类型网络的最短路径路由算法 。特殊类型网络的单播算法 ● 特殊类型网络中的多播算法 ● 虚信道和虚网络 ● 完全自适应和无死锁路由算法 ● 几个自适应和无死锁路由算法 ● 容错单播的一般方法 ● 网格和圆环中的容错单播算法 ● 超立方中的容错单播算法 容错组播算法
第四章 分布式路由算法 ⚫ 分布式路由算法导论 ⚫ 一般类型网络的最短路径路由算法 ⚫ 特殊类型网络的单播算法 ⚫ 特殊类型网络中的多播算法 ⚫ 虚信道和虚网络 ⚫ 完全自适应和无死锁路由算法 ⚫ 几个自适应和无死锁路由算法 ⚫ 容错单播的一般方法 ⚫ 网格和圆环中的容错单播算法 ⚫ 超立方中的容错单播算法 ⚫ 容错组播算法

4.10超立方中的容错单播 按照使用的错误信息类型对超立方中的容错单 播路由进行分类: 。基于局部信息的 。基于有限全局信息的 基于扩展安全等级模型的
4.10 超立方中的容错单播 ⚫ 按照使用的错误信息类型对超立方中的容错单 播路由进行分类: ⚫ 基于局部信息的 ⚫ 基于有限全局信息的 ⚫ 基于扩展安全等级模型的

4.10.1基于局部信息的模型 已经证明, 。对n维立方中的任何两点u和w,如果H(u,w)=k,那 么从u到w恰好有n条点分离路径。其中 。有k条长度为k的路径和(-k)条长度为k+2的路径 ● 若出错组件的数目L小于n,那么用多条路径进 行路由的方法是很直接的。 。消息沿着条点分离路径进行传送,并且其中至少 有一条是好的。 这样,就可通过那条路径到达目标,路径最大长度 是k+2
4.10.1 基于局部信息的模型 ⚫ 已经证明, ⚫ 对n维立方中的任何两点u和w,如果H(u,w)=k,那 么从u到w恰好有n条点分离路径。其中, ⚫ 有k条长度为k的路径和(n-k)条长度为k+2的路径 ⚫ 若出错组件的数目L小于n,那么用多条路径进 行路由的方法是很直接的。 ⚫ 消息沿着n条点分离路径进行传送,并且其中至少 有一条是好的。 ⚫ 这样,就可通过那条路径到达目标,路径最大长度 是k+2

4.10.1基于局部信息的模型 ● chen和shin给出了下面四种容错路由算法: 1. 出错组件小于n-1,不确保有最优路径。 2. 出错组件小于-1,确保有最优路径。 3. 出错组件无限制,不确保有最优路径。 4. 出错组件无限制,确保有最优路径。 ● 第2和第4种情况是所希望的,但相应的算法 会引入特别的开销
4.10.1 基于局部信息的模型 ⚫ chen和shin给出了下面四种容错路由算法: 1. 出错组件小于n-1,不确保有最优路径。 2. 出错组件小于n-1,确保有最优路径。 3. 出错组件无限制,不确保有最优路径。 4. 出错组件无限制,确保有最优路径。 ⚫ 第2和第4种情况是所希望的,但相应的算法 会引入特别的开销

4.10.1基于局部信息的模型 。下面考虑上述第一种情况的算法, 。首先,给出等位序列的定义 。接着,给出消息的表示方法 ·然后,给出算法 最后,举例
4.10.1 基于局部信息的模型 ⚫ 下面考虑上述第一种情况的算法, ⚫ 首先,给出等位序列的定义 ⚫ 接着,给出消息的表示方法 ⚫ 然后,给出算法 ⚫ 最后,举例

4.10.1基于局部信息的模型 等位序列定义 定义:等位序列[d1,d2,,d] 为当前节点与目标节点不同的所有维度(也叫首选维 度,preferred dimension) 例如: 当前节点:0010 目标节点:0111 。注意: 等位序列是[1,3] 。为表示一个消息的目标,等位序列要和消息一起传送 。因当前节点会随着消息的传递而变化,故等位序列也随着变 化
4.10.1 基于局部信息的模型 等位序列定义 ⚫ 定义:等位序列[d1 , d2 , …, dk ] 为当前节点与目标节点不同的所有维度(也叫首选维 度,preferred dimension) ⚫ 注意: ⚫ 为表示一个消息的目标,等位序列要和消息一起传送 ⚫ 因当前节点会随着消息的传递而变化,故等位序列也随着变 化 例如: 当前节点:0 0 1 0 目标节点:0 1 1 1 等位序列是[1,3]

4.10.1基于局部信息的模型 消息的表示 。每个消息都有一个位的向量标志,用以保存“空余 维度(spare dimensions)”。 可以用这些维度来绕过出错组件。 注意: 空余维度就是那些没有在最初的等位序列中出现的维度 源节点发起路由时,标志中的所有位都将清零。 消息的表示: (k,[d1,d2,.,d,消息,标记)。 k为剩余路径长度,k会在消息的发往过程中不断更新 当k变为0时,消息就到达目标了
4.10.1 基于局部信息的模型 消息的表示 ⚫ 每个消息都有一个n位的向量标志,用以保存“空余 维度(spare dimensions)”。 ⚫ 可以用这些维度来绕过出错组件。 ⚫ 注意: 空余维度就是那些没有在最初的等位序列中出现的维度 ⚫ 源节点发起路由时,标志中的所有位都将清零。 ⚫ 消息的表示: (k, [d1 , d2 , …, dk ], 消息, 标记)。 ⚫ k为剩余路径长度, k会在消息的发往过程中不断更新 ⚫ 当k变为0时,消息就到达目标了

4.10.1基于局部信息的模型 算法描述 当节点收到一个消息时,检查k的值以判断自身 是否为消息的目标 若不是,节点将尝试按照剩下的等位序列中指定的维 度发送消息 每个节点都将努力沿着最短路径发送消息。 然而,若通往最短路径的维度的那些连接出错,这个 节点将使用空余维度通过另外的路径发送消息
4.10.1 基于局部信息的模型 算法描述 ⚫ 当节点收到一个消息时,检查k的值以判断自身 是否为消息的目标 ⚫ 若不是,节点将尝试按照剩下的等位序列中指定的维 度发送消息 ⚫ 每个节点都将努力沿着最短路径发送消息。 ⚫ 然而,若通往最短路径的维度的那些连接出错,这个 节点将使用空余维度通过另外的路径发送消息

4.10.1基于局部信息的模型 算法的描述 初始,等位序列为由源和目标地 址异或得到的所有首选维度, P(u)::=[initiate-routing-process 空余维度的所有位清零。 send ([di,d2,...,d,m,0)to P(u) 口receive(k,d,2,,d],message,tag)+ k =0-save (message) ok≠O→intermediate-node intermediate-node::= 每个节点努力沿着最短路径传送 [The djth(1≤j≤k)link and neighbor are both healthy→ [send(k-1,[d,…,d-1,d+1,,d4k], message,tag)to u(d;) 注意:u0)表示沿着 维度i的u的邻居。 No link and neighbor are both healthy [V1≤i≤x \tag(di):=1: tag(h)=l,where h=min{i:tag(i)=0,1≤t≤n}: send (k +1,[di.d2,...,d,h],message,tag)to u(h) ]
4.10.1 基于局部信息的模型 算法的描述 注意:u (i)表示沿着 维度i的u的邻居。 初始,等位序列为由源和目标地 址异或得到的所有首选维度, 空余维度的所有位清零。 每个节点努力沿着最短路径传送
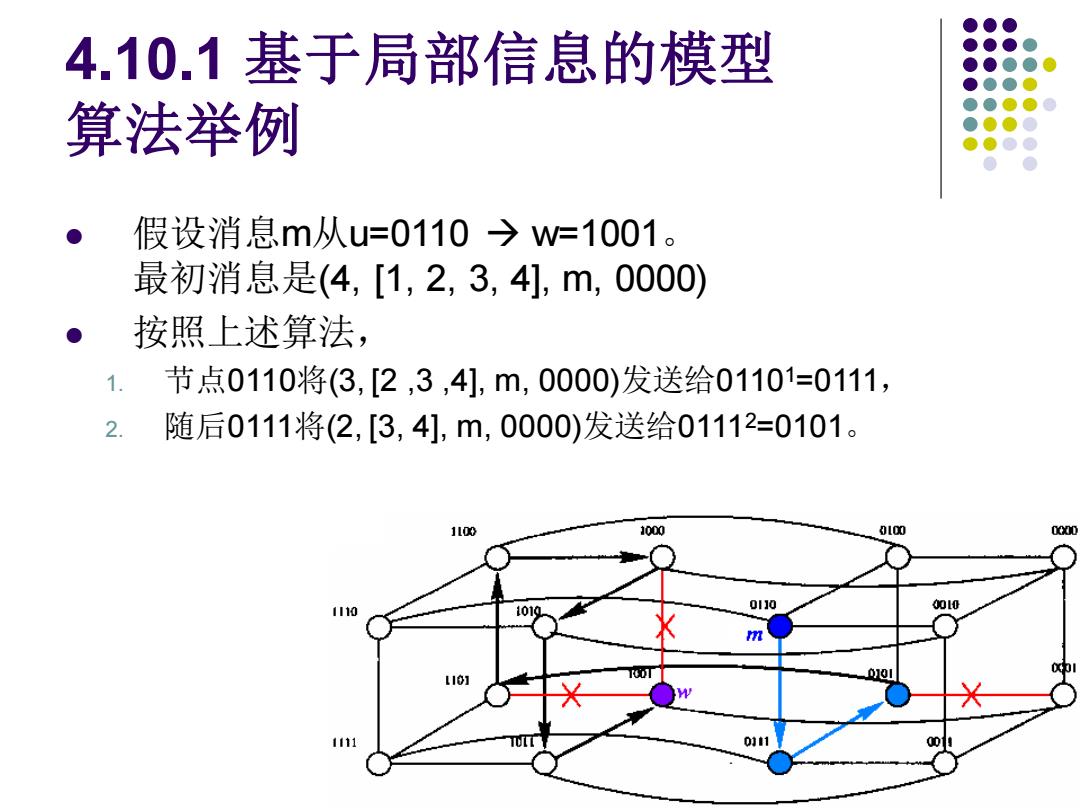
4.10.1基于局部信息的模型 算法举例 假设消息m从u=0110→w=1001。 最初消息是(4,[1,2,3,4],m,0000) 按照上述算法, 1. 节点0110将(3,[2,3,4],m,0000)发送给01101=0111, 2. 随后0111将(2,[3,4],m,0000)发送给01112=0101。 1l00 1000 0100 00a0 1110 1010 0110 010 m 1111 011 oos
4.10.1 基于局部信息的模型 算法举例 ⚫ 假设消息m从u=0110 → w=1001。 最初消息是(4, [1, 2, 3, 4], m, 0000) ⚫ 按照上述算法, 1. 节点0110将(3, [2 ,3 ,4], m, 0000)发送给01101=0111, 2. 随后0111将(2, [3, 4], m, 0000)发送给01112=0101