
2.2 函数的求导法则01函数和、差、积、商的求导法则02反函数求导法则03复合函数求导法则04高阶导数
01 函数和、差、积、商的求导法则 02 反函数求导法则 03 复合函数求导法则 04 高阶导数 2.2 函数的求导法则

00函数和、差、积、商的求导法则设函数u(x),v(x)在点x处可导,则函数u(x)±v(x),定理2.3u(x)u(x) ×(x), u-(v(x)1 0)在点x处也可导,且v(x)()[u(x)±v(x)= udx)±vx) ;(2)[u(x)v(x)= udx)v(x) + u(x)vax) ;él ucéu(x) uevdx)udx) x(x) - u(x)dx)特别地,33v(x)13v(x)v (x)v?(x)
一、 函数和、差、积、商的求导法则 2 定理2.3

#一函数和、差、积、商的求导法则设函数u(x),v(x)在点x处可导,利用定义证明例(1) [u(x)v(x)= uax)v(x) + u(x)vdx);(2)设函数u(x),u,(x),u(x)L u,(x)可导f(x)=u(x)u(x)L u,(x),写出f(x)的求导公式0解
一、 函数和、差、积、商的求导法则 3 例 1 解

O00函数和、差、积、商的求导法则法则(1)(2)可以推广到任意有限个可导函数相加减和相乘的情形注(u±v±w)e=uctvetwe(uvw)e=udw+vaw+wan特别地,JCu(x)=Cudx)(C为常数);
一、 函数和、差、积、商的求导法则 4 注

OA函数和、差、积、商的求导法则TT例(1)设f(x) = 4cosx - x3 + 3sinx - sin=,求f'(x)及f'(0)2
一、 函数和、差、积、商的求导法则 5 例 2
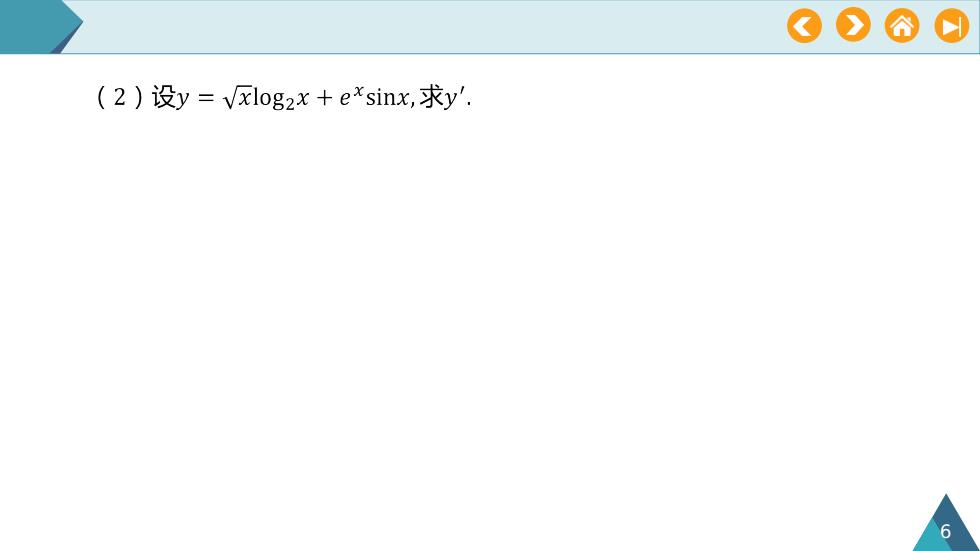
??(2)设y = Vxlog2x +e~sinx,求y'6
6
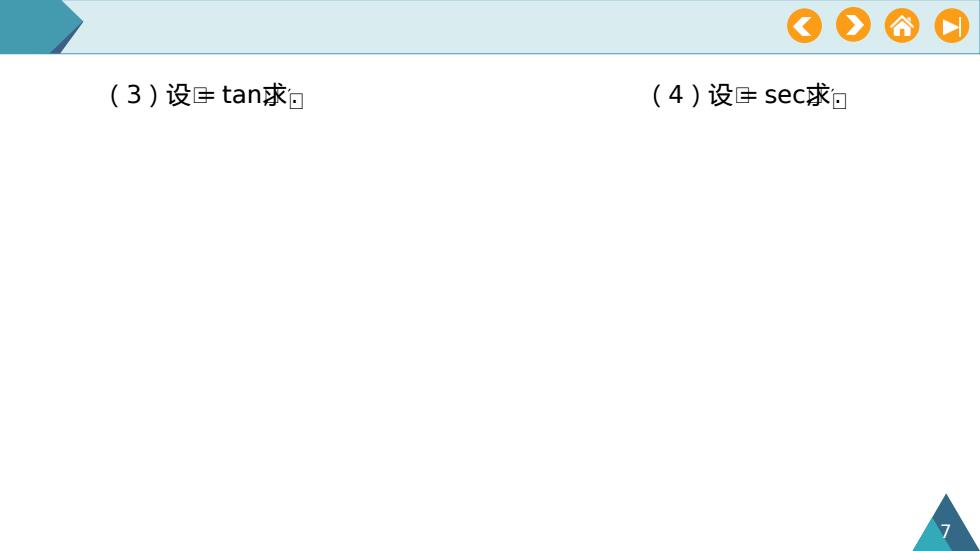
OOA0(3)设tan求(4)设sec求
7 (3)设ᵆ= tanᵆ, ᵆ′. (4)设ᵆ= secᵆ, ᵆ′

2.2 函数的求导法则函数和、差、积、商的求导法则0102反函数求导法则03复合函数求导法则04高阶导数
函数和、差、积、商的求导法则 反函数求导法则 03 复合函数求导法则 04 高阶导数 02 01 2.2 函数的求导法则

O?0反函数求导法则若函数x=f(y)在区间I.内单调可导且每一点都fdy)I0定理2.4则它的反函数y=f-(x)在相应区间I、内也单调可导1且有有[Lf-(x)le=fdy)11Dydy或limDxdxdxDrR 0DxlimdyDyRODy即反函数的导数等于直接函数导数的倒数9
二、 反函数求导法则 9 定理2.4

OA反函数求导法则证明(arcsinx)4V1- x心证同理(arccosx)e=(arct cot x)e-arctanx)1+x
二、 反函数求导法则 10 例 3 证