
山东理工大学数学与统计学院SCHOOLOFMATHEMATICSANDSTATISTICSSHANDONGUNIVERSITYOFTECHNOLOGY高等数学李海玲
高 等 数 学 李 海 玲
高等数学简介什么是高等数学研究内容及方法三、「高等数学有什么用四、学习方法五、注意事项
高等数学简介 一、什么是高等数学 二、研究内容及方法 三、高等数学有什么用 四、学习方法 五、注意事项

一、什么是高等数学初等数学一研究对象为常量,以静止观点研究问题高等数学一研究对象为变量,运动和辩证法进入了数学数学中的转折点是苗卡尔的变数有了变数,运动进入了数学。有了变数,辩证法进入了数学,有了变数,微分和积分也就立刺成恩格斯为必要的了,而它们也就立刻刺产生
一、什么是高等数学 初等数学 — 研究对象为常量,以静止观点研究问题. 高等数学 — 研究对象为变量,运动和辩证法进入了数学. 数学中的转折点是笛卡尔的变数. 有了变数 , 运动进入了数学, 有了变数,辩证法进入了数学 , 有了变数 , 微分和积分也就立刻成 恩格斯 为必要的了,而它们也就立刻产生

二、研究内容①函数、极限与连续①一元函数微分学①一元函数积分学①多元函数微分学①多元函数积分学①向量代数与空间解析几何①无穷级数
二、研究内容 Ø 函数、极限与连续 Ø 一元函数微分学 Ø 一元函数积分学 Ø 多元函数微分学 Ø 多元函数积分学 Ø 向量代数与空间解析几何 Ø 无穷级数

切线、图形面积、体积旧应用速度...、作功.元素法中值定理微分学分学一无函数微积分无穷分析极限连续级数引论常微分个函数方程空间解析几何多元函数多元函数多元函类多元函数微积分积分学微分学切线、法平面、曲面面积、体积应用梯度.质心
导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 切线、法平面、 梯度. 曲面面积、体积、 质心. 空间解析几何 无穷 级数 常微分 方程 一元函数微积分 多元函数微积分
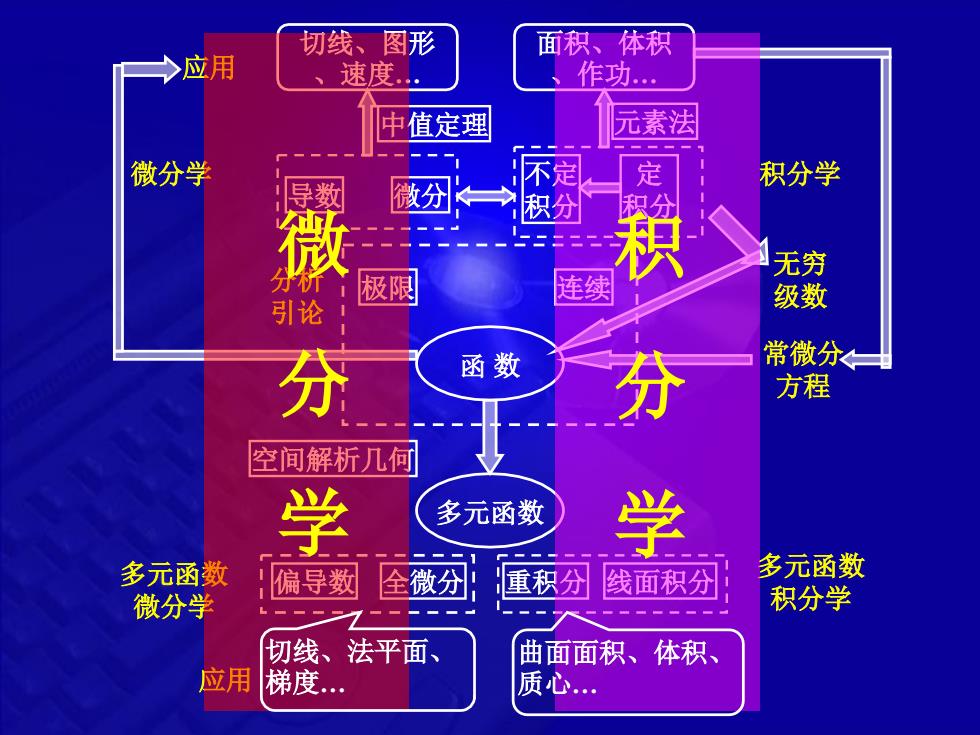
面积、体积切线、图形一应用速度.作功。元素法中值定理慌蔻定积分学微分学导数微积分积分微分积无穷极限连续级数常微分←函数分学方程空间解析几何学多元函数多元函数多元函数偏导数分微分重积线面积分全积分学微分学切线、法平面曲面面积、体积、应用梯度...质心
导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 空间解析几何 无穷 级数 常微分 方程 微 分 学 积 分 学 切线、法平面、 梯度. 曲面面积、体积、 质心
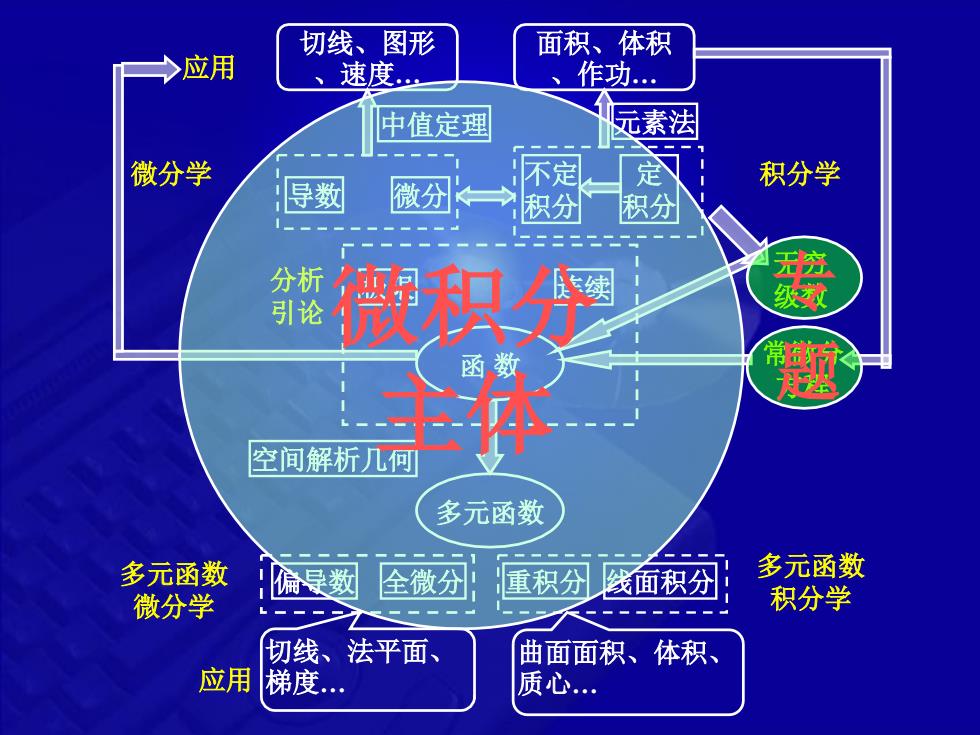
切线、图形面积、体积二>应用速度作功...元素法中值定理不定定微分学积分学导数微分积分积分专分析续微积分引论题函数主体空间解析几何多元函数多元函数多元函数偏导数线面积分全微分重积分积分学微分学切线、法平面曲面面积、体积、应用梯度...质心
导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 空间解析几何 无穷 级数 常微分 方程 微积分 主体 专 题 切线、法平面、 梯度. 曲面面积、体积、 质心
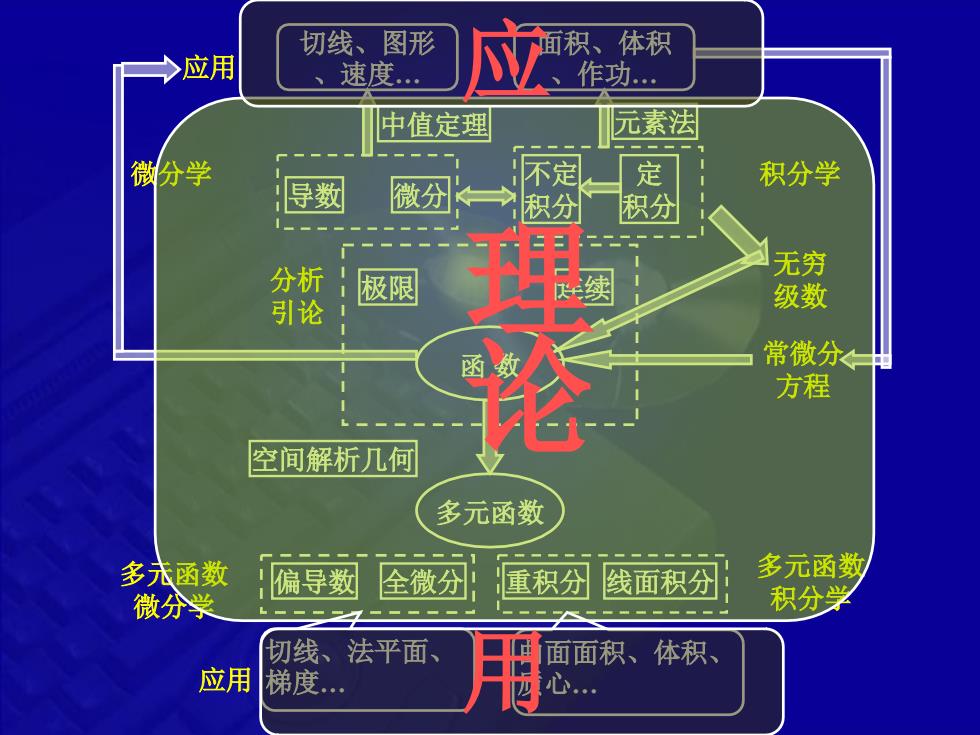
应面积、体积切线、图形一>应用速度作功..元素法中值定理不定定积分学微分学数微分积分积分理伦无穷分析极限续级数引论常微分个函方程空间解析几何多元函数多元函数多未函数偏导数线面积分全微分重积分积分学微分学切线、法平面、面面积、体积、应用梯度.心L
导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 空间解析几何 无穷 级数 常微分 方程 理 论 切线、法平面、 梯度. 曲面面积、体积、 质心. 应 用

切线、图形面积、体积二>应用速度...、作功...元素法中值定理不定定积分学微分学数微分积分积分无穷分析极限连续级数引论常微分←函数方程空间解析几何多元函数多元函数多元函数偏导数线面积分全微分重积分积分学微分学切线、法平面曲面面积应用梯度...体积、质心
导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 切线、法平面 、梯度. 曲面面积 体积、质心. 空间解析几何 无穷 级数 常微分 方程

极限方法
极限方法