《线性代数》课程教学资源（课件讲稿，C）第四章 4-1线性方程组有解的判定

第四章线性方程组第一节线性方程组解的判别

第四章 线性方程组 第一节 线性方程组解的判别

第四章线性方程组3xi -2x2 =12,有唯一解（2，-3)2x + X2 = 1.3x -2x2 = 12,无解3x - 2x2 = 6.3xi -2x2 = 12,无穷多解6xi - 4x2 = 24

第四章 线性方程组        2 1. 3 2 12, 1 2 1 2 x x x x 1 2 1 2 3 2 12, 3 2 6. x x x x        1 2 1 2 3 2 12, 6 4 24. x x x x        有唯一解（2，-3） 无解 无穷多解

第四章线性方程组-311-2123x) -2x2 =12, (3-2170(22xi +x2 = 1.123-23123x - 2x2 =12,2-6363x - 2x2 = 6.-2123-2123-23x -2x2 =12,002406-46x - 4x2 = 24

第四章 线性方程组        2 1. 3 2 12, 1 2 1 2 x x x x 1 2 1 2 3 2 12, 3 2 6. x x x x        1 2 1 2 3 2 12, 6 4 24. x x x x        3 2 12 6 4 24         3 2 12 3 2 6         3 2 12 2 1 1        3 2 12 0 0 0        3 2 12 0 0 6         1 3 11 2 1 1        1 3 11 0 7 21        

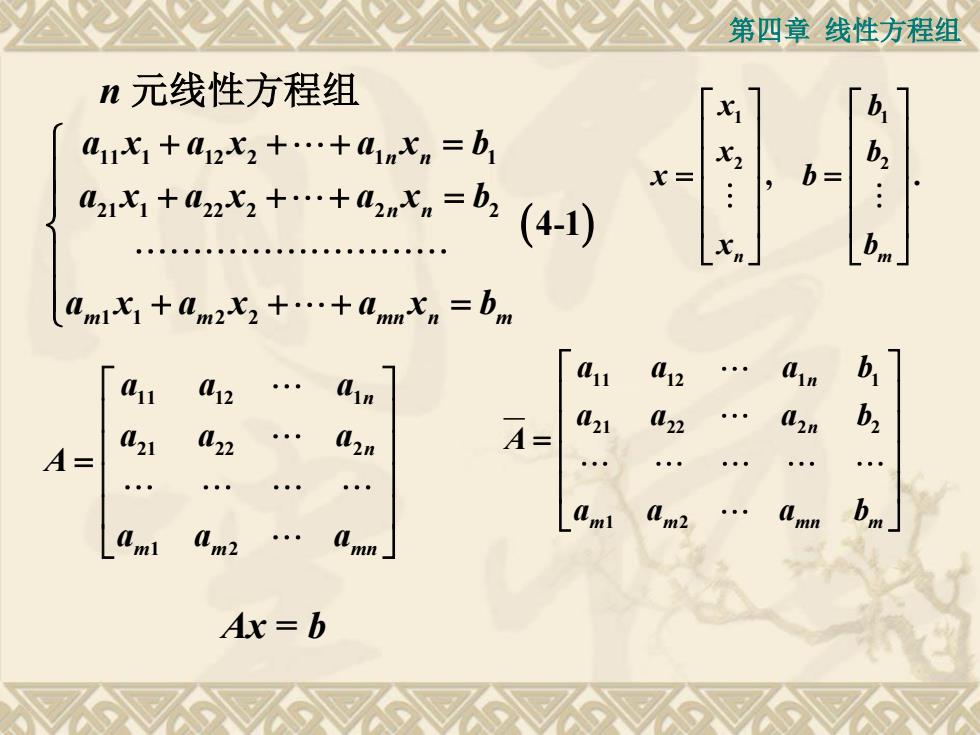
第四章线性方程组n元线性方程组b,xiaux, +ax, +...+anx, =bbX2x=ba21x, +a22x, +...+a2nx, =(4-1)bmamX, +am2x,+..+amx,=b,mb,ala12ala12inb,a211222A=a21(2242nA=b.amlam2ammaaamlm2mnAx = b

第四章 线性方程组 n 元线性方程组   11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 4-1 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b                    11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a              1 1 2 2 , . n m x b x b x b x b                           Ax = b 11 12 1 1 21 22 2 2 1 2 n n m m mn m a a a b a a a b A a a a b             

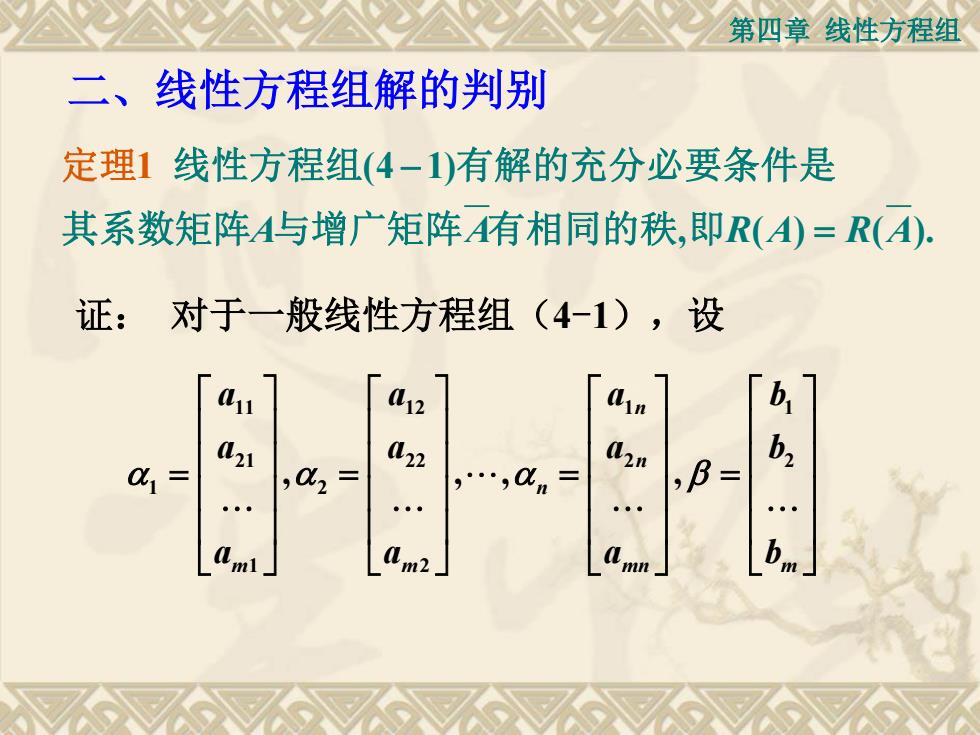
第四章线性方程组二、线性方程组解的判别定理1线性方程组（4一1)有解的充分必要条件是其系数矩阵A与增广矩阵A有相同的秩,即R(A)=R(A)证：对于一般线性方程组（4-1），设b,(1la12ainb,a21(22d2n,B=,α2αbaa0m2mlmnm

第四章 线性方程组 二、线性方程组解的判别 (4 1) , ( ) ) 1 A A R A R A( .   线性方程组 有解的充分必要条件是 其系数矩阵 与增广矩阵 有相同的秩 即 定理 证： 对于一般线性方程组（4-1），设 11 12 1 1 21 22 2 2 1 2 1 2 , , , , n n n m m mn m a a a b a a a b a a a b                                                            

第四章线性方程组则线性方程组（4-1）可写为x,α +x,α, +...+x,αn = β (4-3)并且1A=[α α, ... αnA=[α α, ... α β]

第四章 线性方程组 则线性方程组（4-1）可写为 1 1 2 2 (4 3) n n x x x         1 2 1 2 n n A A                    并且

第四章线性方程组推论1 当R(A)± R(A)时，方程组(4-1)无解推论2如果方程组(4一1)有解，则它有惟一解的充分必要条件是R(A)=R(A)=n推论3如果方程组(4-1)有解，且R(A)= R(A)<n.则方程组（4-1)有无穷多解

第四章 线性方程组 推论1 ( ) ( ) (4 1 当R A R A   时，方程组 ) . 无解 (4 1) ( ) ( ) . 2 R A R A n    如果方程组 有解，则它有惟一解的 充分必要条件是 推论 (4 1) ( ) ( ) , (4 1) . 3    R A R A n  如果方程组 有解，且 则方程组 有 推 无穷多解 论

第四章线性方程组-2x +x2 +x = -2例、方程组x一2x+x，=元当取何值时有解？Xi +x2 -2x, = 3并求其全部解解：对方程组的增广矩阵A实施初等行变换2212-211-2rAr2A=S1 -212-2-2 222222-2-2r-r+-2-23-330-30+2r00300-2+212-2++222-3

第四章 线性方程组 2 2 1 1 2 1 2 1 1 1 2 A                  1 3 ~ r r  2 1 1 2 1 2 1 2 1 1 2                 2 1 3 1 ~ 2 r r r r   解： 对方程组的增广矩阵A实施初等行变换， 2 2 2 1 1 2 0 3 3 0 3 3 2 2                     3 2 ~ r r  2 2 2 1 1 2 0 3 3 0 0 0 2                      1 2 3 1 2 3 2 1 2 3 2 2 2 2 x x x x x x x x x                   例、方程组 当 取何值时有解？ 并求其全部解