《线性代数》课程教学资源（课件讲稿，C）第三章 3-1矩阵的运算

第三章矩阵的运算$ 3.1矩阵的运算

第三章 矩阵的运算 §3.1 矩阵的运算

第三章矩阵的运算同型矩阵：：行数与列数分别相等的矩阵矩阵相等：A=(aj)mxn,B=(bj)mxn’ 且ai, =b, = A=B(i=1,..,m;j=l,...,n)

第三章 矩阵的运算 同型矩阵：行数与列数分别相等的矩阵 矩阵相等: ( ) , ( ) ( 1, , ; 1, , ) A a B b a b A B ij m n ij m n ij ij i m j n   = = =  = = = ，且

第三章矩阵的运算一、矩阵加法定义1 设矩阵A=(aj)mx,B=(b,）mxn，称矩阵C =(a; + bi,)mxn为矩阵A与矩阵B的和，记作C=A+B32+1-1+0-10-1C=A+B=/1-22+3-2+15-1-1

第三章 矩阵的运算 一、矩阵加法 ( ) , ( ) ( ) . 1 ij m n ij m n ij ij m n A a B b C a b A B C A B    = = = + = + 设矩阵 ，称 矩 阵 为矩阵 与矩阵 的 和，记 作 定 义 2 1 0 1 1 0 3 1 1 1 2 2 3 2 1 1 5 1 C A B     + − − + − − = + = =         − + − + − −

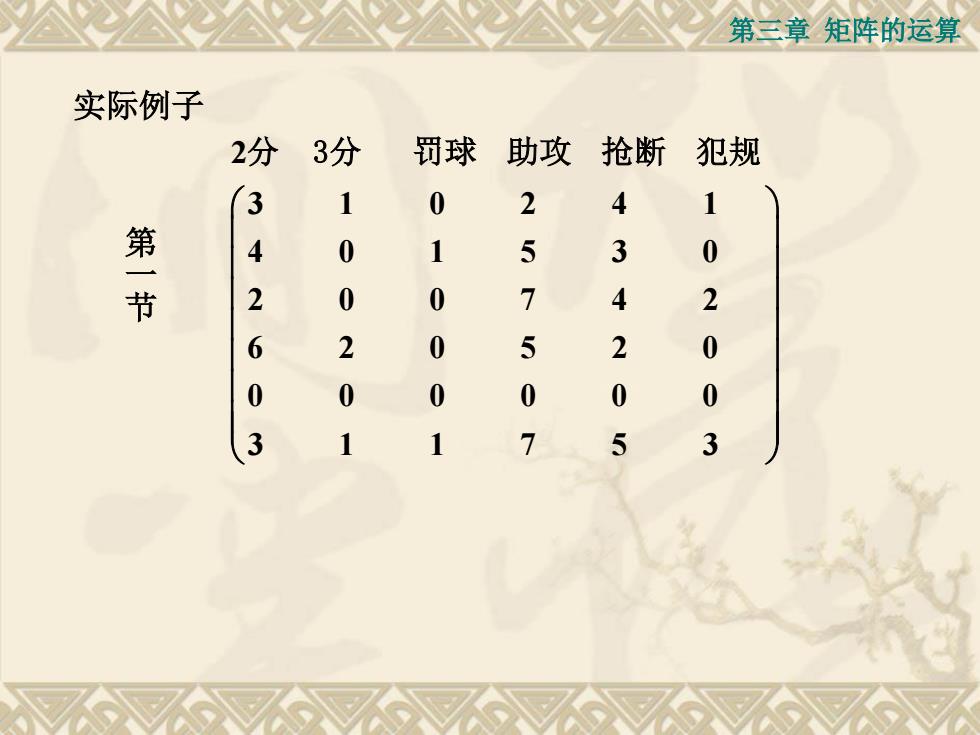
第三章矩阵的运算实际例子3分2分罚球助攻抢断犯规1310241第一节4530022160520200000033751

第三章 矩阵的运算 2 3 1 0 2 4 1 4 0 1 5 3 0 2 0 0 7 4 2 6 2 0 5 2 0 0 0 0 0 0 0 3 1 1 7 5 3       分 3分 罚球 助攻 抢断 犯规 第一节 实际例子

第三章矩阵的运算零矩阵：元素全是零的矩阵称为零矩阵.记作：0负矩阵：设A=(a）mxn，则称矩阵-(a）mxn为A的负矩阵记作- A, 即- A =-(a,)mxn

第三章 矩阵的运算 零矩阵：元素全是零的矩阵称为零矩阵.记作: O ( ) ( ) ( ) . ij m n ij m n ij m n A a a A A A a    = − − − = − 设 ,则称矩阵 为 的负矩阵 记作 ，即 负矩阵：

第三章矩阵的运算矩阵加法的性质：A,B,C,O 均为m×n矩阵1. A+B=B+A2. (A+B)+C = A+(B+C)3. A+0=0+A=A4. A+(-A)=(-A)+A =05.矩阵减法A-B= A+(-B)=(a; -b,)mxn

第三章 矩阵的运算 矩阵加法的性质： A B C O m n , , , 均 为  矩 阵 1 . A + B = B + A 2 . ( A + B ) + C = A + ( B + C ) 3 . A + O = O + A = A 4 . A + ( − A ) = ( − A ) + A = O 5. ( ) ( ) A B A B a b ij ij m n − = + − = − 矩 阵 减 法

第三章矩阵的运算使得例1求矩阵X,023+X=解：023X=022221-31121

第三章 矩阵的运算 1 1 2 3 1 0 1 2 3 2 0 1 2 3 0 1 1 1 1 0 1 1 2 2 0 X X     − −     + = −             − − − 例 求矩阵 ，使得 解： 0 1 2 3 1 2 3 1 3 0 1 1 2 0 1 2 1 2 2 0 1 1 0 1 X     − −     = − −             − − − 1 3 1 4 1 0 0 3 2 1 2 1   − − −   = −       −

第三章矩阵的运算二、数与矩阵的乘法定义2 设矩阵A=(aj)mxn，π是一个数,矩阵(αa,）mxn称为数与矩阵A的乘积，记作A或Aa,即aA= AA=(aag)mxn

第三章 矩阵的运算 二、数与矩阵的乘法 ( ) , , ( ) ( ) 2 ij m n ij m n ij m n A a a A A A A A a            = = = 数 与 设矩阵 是一个数 矩阵 称为 记作 或 ， 即 矩阵 的 定 乘积， 义

第三章矩阵的运算数乘的性质：设A，B是m×n矩阵，a,u是数1. a(uA) =(aμ)A2. (a+μ)A=aA+uA3.2(A+B)=2A+2B4.1A=A5.0A=06.(-1)A=-A

第三章 矩阵的运算 数乘的性质： 2. ( )     + = + A A A 设 A B m n ， 是  矩 阵 ，  , 是 数 3. ( )    A B A B + = + 1. ( ) ( )    A A = 4. 1A A = 5. 0A O= 6. ( 1) − = − A A

第三章矩阵的运算20例2 设A =B=-2336求2A-B+福91236解：4-1-10+1+2-2-0+12A-B+C34-3-2 -4-1+32+2+4238-2一

第三章 矩阵的运算 2 0 1 1 1 0 2 , , 1 2 2 2 3 1 3 6 3 1 2 12 6 9 3 A B C A B C     − − = =         − −   − = − +     − 例 设 ,求 1 4 1 1 0 1 2 2 0 1 2 3 2 2 4 4 3 2 4 1 3 A B C   − − + + − − + − + =     + + − − − − + 2 3 1 8 1 2   − =     − − 解：