
第二节行列式的性质目的要求:掌握行列式的性质熟练运用行列式的性质化行列式为三角行列式加油!
第二节 行列式的性质 目的要求: 掌握行列式的性质 熟练运用行列式的性质 化行列式为三角行列式

一n阶行列式的定义的推广定理1n阶行列式等于它的任意一行(列)的各个元素与其对应的代数余子式的乘积之和,即有D= ai,Ai +...+ai,A, +...+ainAin i=l,2,..,n或者D=ai+a..A.Aj=1,2,..,n-0加油!
D ai1 Ai1 aijAij ainAin i 1,2, ,n 或者 D a1 j A1 j aijAij an jAn j j 1,2, ,n 一、 n阶行列式的定义的推广 定理1 n阶行列式等于它的任意一行(列)的各个元素 与其对应的代数余子式的乘积之和,即有

二、行列式的性质加油!
二、行列式的性质
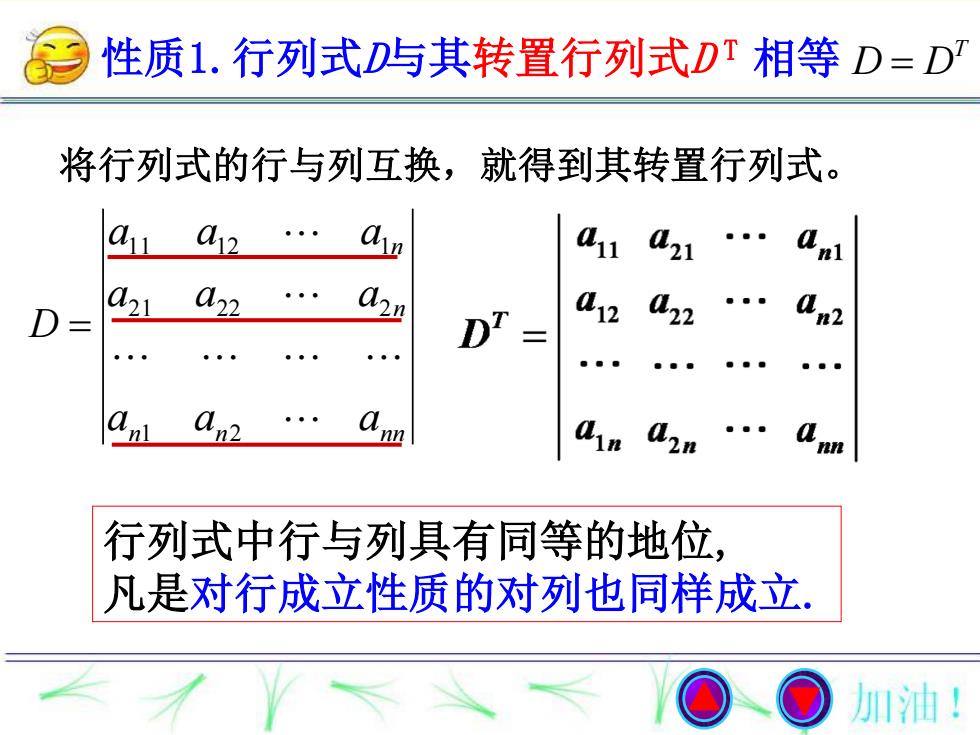
相等性质1.行列式D与其转置行列式DTD=D将行列式的行与列互换,就得到其转置行列式。a1221nlOa12Q7122n2a0ann2nlnnn行列式中行与列具有同等的地位凡是对行成立性质的对列也同样成立加油!
性质1.行列式D与其转置行列式D T 相等 n n nn n n a a a a a a a a a D 1 2 21 22 2 11 12 1 将行列式的行与列互换,就得到其转置行列式。 行列式中行与列具有同等的地位, 凡是对行成立性质的对列也同样成立. T D D

性质2.行列式交换两行位置,值变号a(2211iai2a012mdaaa2inaaaaan2nln2nnnnn加油!
性质2. 行列式交换两行位置,值变号. 11 12 1 1 2 1 2 1 2 n i i in j j jn n n nn a a a a a a a a a a a a 11 12 1 1 2 1 2 1 2 n j j jn i i in n n nn a a a a a a a a a a a a

推论.行列式中有两行元素对应相等行列式的值为零2242202加油!
推论 .行列式中有两行元素对应相等, 行列式的值为零. 1 2 1 2 1 0 2 3 2 4 1 0 2

性质3.行列式某一行的所有元素都乘以同一数k.等于用数k乘以此行列式a1rnKkaaila;2Cininaaaaaan2nn2nnnlnn加油!
性质3. 行列式某一行的所有元素都乘 以同一数k,等于用数k乘以此行列式。 n n nn i i in n a a a ka ka ka a a a 1 2 1 2 11 12 1 n n nn i i in n a a a a a a a a a 1 2 1 2 11 12 1 k

推论行列式中某一行的元素的公因子可以提到行列式的外面推论.行列式中某一行的元素全为零,则行列式为零27C0福2加油!
推论. 行列式中某一行的元素的公因子可 以提到行列式的外面. 推论. 行列式中某一行的元素全为零,则 行列式为零. 1 7 2 0 0 0 1 6 2

推论.行列式中两行元素对应成比例,则行列式为零22-1一397972= 2 ×22-24-1 加油!
推论. 行列式中两行元素对应成比例,则 行列式为零. 1 1 2 1 1 2 3 7 9 2 3 7 9 2 2 4 1 1 2

则该性质4.若行列式中某行元素为两数和,行列式可拆成相应的两个行列式的和WWn3-2+54+7Ain +b.Aiz +bi2..i, +bi,0aannLaua121b;bbai2inilinaaaan2ninnnln2nn加油!
性质4. 若行列式中某行元素为两数和,则该 行列式可拆成相应的两个行列式的和. 11 12 1 1 1 2 2 1 2 n i i i i in in n n nn a a a a b a b a b a a a 11 12 1 1 2 1 2 n i i in n n nn a a a a a a a a a 11 12 1 1 2 1 2 n i i in n n nn a a a b b b a a a 1 3 1 3 1 3 = -2+5 4 7 2 4 5 7