华北电力大学：《电气工程》实验教学资源（PPT课件讲稿）系统实验室多媒体课件——暂态上机计算

暂态上机计算

暂态上机计算

计算机计算复杂系统短路电流交流 分量初始值的原理 ·计算短路电流"实质上就是求解交流电路的稳态 电流，其数学模型也就是网络的线性代数方程组， 一般选用网络节点方程，即用节点阻抗矩阵或节 点导纳矩阵描述的网络方程。 ·以下将先介绍短路计算用的等值网络。 ·然后分别给出用节点阻抗矩阵和节点导纳矩阵计 算短路电流和电网任意处电压及电流的公式

计算机计算复杂系统短路电流交流 分量初始值的原理 • 计算短路电流 实质上就是求解交流电路的稳态 电流，其数学模型也就是网络的线性代数方程组， 一般选用网络节点方程，即用节点阻抗矩阵或节 点导纳矩阵描述的网络方程。 • 以下将先介绍短路计算用的等值网络。 • 然后分别给出用节点阻抗矩阵和节点导纳矩阵计 算短路电流和电网任意处电压及电流的公式。 I

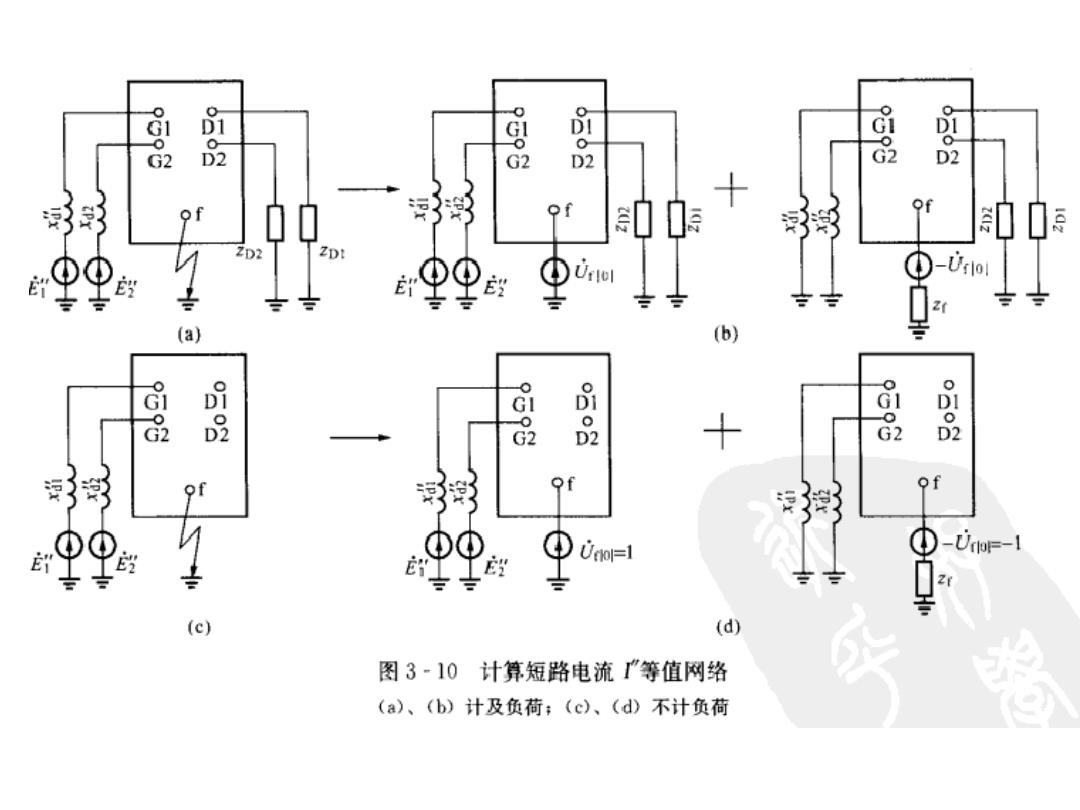
品 D2 说影 00 r④9 D-Uslo (a) (b) G 品 G2 品2 of 昂 ①-U-l (c) (d) 图3·10计算短路电流'等值网络 (a)、(b)计及负荷；(c)、(d)不计负荷

二、 用节点阻抗矩阵表示的节点电压 方程 Z11 02 Z22 。。。 Un Z n2 In 节点阻抗矩阵的对角元素Z(1=1,2,n)称自阻抗，其大 小等于经节点注入单位电流=1，其余节点全部开路时，节 点1上的电压。自导纳Z亦可以看成从节点向整个网络看进 去的对地等值阻抗。 节点阻抗矩阵的非对角元素Z(i=1,2n,j=1,2,n, )称互阻抗或称转移阻抗，其大小等于经节点注入单位 电流仁，其余节点全部开路时，节点上的电压。 ,且满足Z,=Z,即节点阻抗矩阵为对称矩阵

二、用节点阻抗矩阵表示的节点电压 方程 • 节点阻抗矩阵的对角元素Zii（i =1,2,…,n）称自阻抗，其大 小等于经节点i注入单位电流I i=1，其余节点全部开路时，节 点i上的电压。自导纳Zii亦可以看成从节点i向整个网络看进 去的对地等值阻抗。 • 节点阻抗矩阵的非对角元素Zij（i =1,2,…,n，j =1,2,…,n， i≠j）称互阻抗或称转移阻抗，其大小等于经节点i注入单位 电流I i=1，其余节点全部开路时，节点j上的电压。 • 且满足Zij=Zji，即节点阻抗矩阵为对称矩阵。                           =               n n n n n n n n I I I U U U                2 1 1 2 2 1 2 2 2 1 1 1 2 1 2 1 Z Z Z Z Z Z Z Z Z

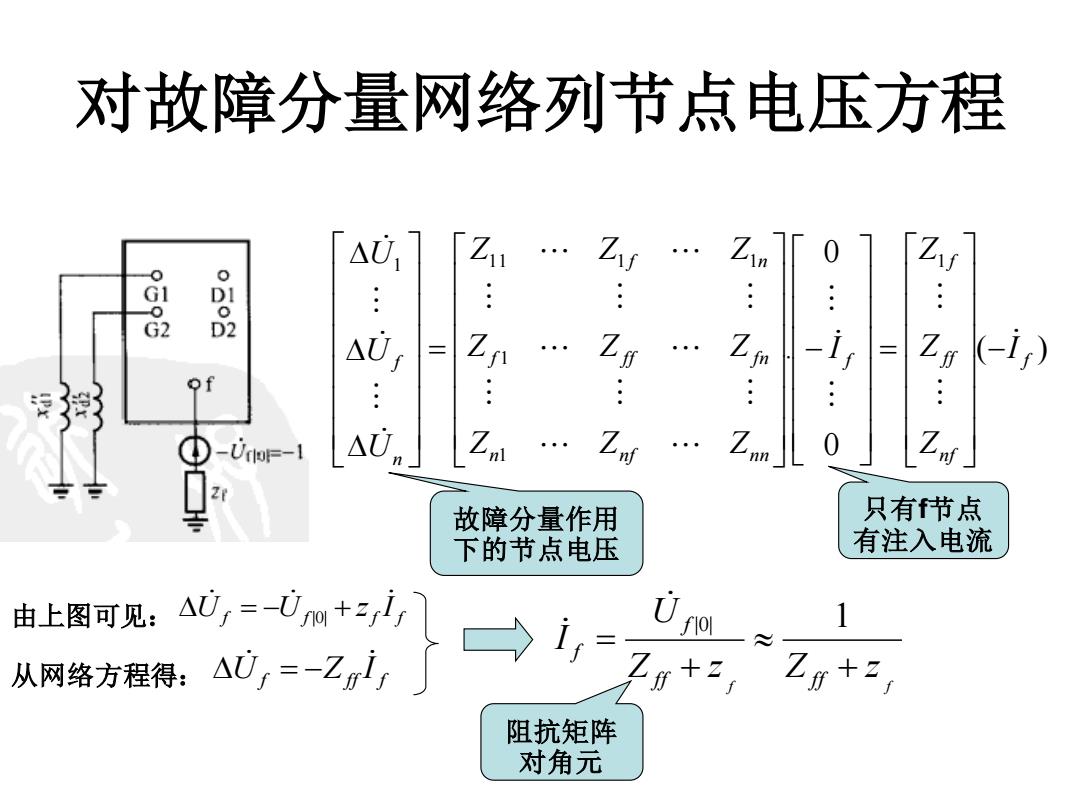
对故障分量网络列节点电压方程 △U1 Z11… 0 1 8 : G2 Zn -i) of : : : -UrF-1 △Um … Z 0 故障分量作用 只有节点 下的节点电压 有注入电流 U1 图阿现400+之Z,+,7一 ≈ 从网络方程得：△0r=-Z1,」 m+2 阻抗矩阵 对角元

对故障分量网络列节点电压方程 ( ) 0 0 . 1 1 1 1 1 1 1 1 f n f f f f f n n f n n f f f f n f n n f I Z Z Z I Z Z Z Z Z Z Z Z Z U U U                        −                 =                 −                 =                    故障分量作用 下的节点电压 只有f节点 有注入电流 从网络方程得： f ff f U Z I   = −  由上图可见： f f f f U U z I   = −  +  |0| f f Z z Z z U I ff ff f f +  + = |0| 1   阻抗矩阵 对角元

如果忽略z+ 各节点短路后的电压为：（假设故障前各个节点电压为） U=Uno+AU=Uno-Zi =1-Zi! 0,=0e+A0,=y U,=Un+AU,=Un-Zwy =1-Zwir 任一支路的电流为： 0.-0A0-A01=(40,-A0,)y 2

f f Z z Z z U I ff ff f f +  + = |0| 1   ff f Z I 1   n n n n n f n f f f f f f f f f f U U U U Z Z I U U U z I U U U U Z Z I               = +  = −  − = +  = = +  = −  − 1 1 0 0 0 1 1 0 1 1 0 1 1 如果忽略zf i j i j i j i j i j i j i j U U y z U U z U U I ( )        =  −  −  − = 各节点短路后的电压为：（假设故障前各个节点电压为1） 任一支路i-j的电流为：

如何求节点阻抗矩阵的元素 Zu Z12 0 7 7 7 1 f2 f2 U Zn 0 Zr~Zf 就是在f点通以单位电流（其他节点电流均为零）时1~n点的电压U,~)

如何求节点阻抗矩阵的元素                         =                           =               0 1 0 I I I U U U                        n n n n f f f n n n f n n n n f f f n n n f Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z 1 2 1 2 1 1 1 2 1 1 1 2 1 2 1 1 1 2 1 1 Z1 f ~ Znf 就是在f点通以单位电流（其他节点电流均为零）时1~n点的电压 U UN   1 ~

用节点导纳矩阵求1~n点电压 0 0 fn : 已知：节点导纳矩阵，点注入电流为1，求节点电压。 解这个线性方程组的方法： （1)高斯消去法； 本次设计直接用 (2)三角分解法； MATLAB解线性代 (3)因子表法 数方程

用节点导纳矩阵求1~n点电压                 =                 =                                 0 1 0 0 0 . 1 1 1 1 1 1 1                       f n f n n f n n f f f f n f f I U U U Y Y Y Y Y Y Y Y Y 已知：节点导纳矩阵，f点注入电流为1，求节点电压。 解这个线性方程组的方法： （1）高斯消去法； （2）三角分解法； （3）因子表法 本次设计直接用 MATLAB解线性代 数方程

进行短路电流计算的步骤 (1)输入已知数据：网络结构与线路参数，故障前 各节点电压（由潮流计算得)，故障点。 ● (2)形成节点导纳矩阵，由此计算Zy~Z ● (3)计算短路电流i, ● (4)计算各节点故障分量电压 ● (5)计算故障后全电压=故障前电压+故障分量电 压 ·(6)计算任意支路电流

进行短路电流计算的步骤 • （1）输入已知数据：网络结构与线路参数，故障前 各节点电压（由潮流计算得），故障点。 • （2）形成节点导纳矩阵，由此计算 • （3）计算短路电流 • （4）计算各节点故障分量电压 • （5）计算故障后全电压=故障前电压+故障分量电 压 • （6）计算任意支路电流 Z1 f ~ Znf f I 

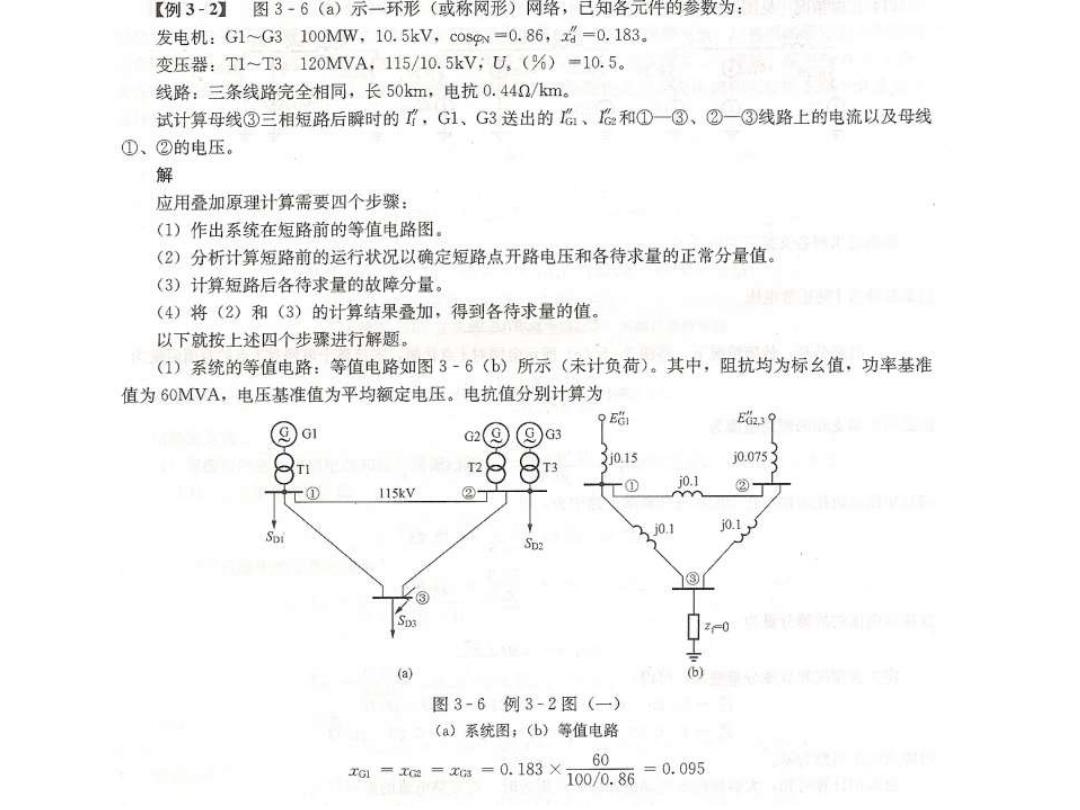
【例3-2】图3·6(a)示一环形（或称网形）网络，已知各元件的参数为 发电机：G1~G3100MW,10.5kV,cosp=0.86,x名=0.183。 变压器：T1~T3120MVA,115/10.5kV,U,(%)=10.5。 线路：三条线路完全相同，长50km,电抗0.44n/km。 试计算母线③三相短路后瞬时的疗，G1、G3送出的治、总和①一③、②一③线路上的电流以及母线 ①、②的电压。 解 应用叠加原理计算需要四个步骤： (1)作出系统在短路前的等值电路图. (2)分析计算短路前的运行状况以确定短路点开路电压和各待求量的正常分量值。 (3)计算短路后各待求量的故障分量。 (4)将(2)和(3)的计算结果叠加，得到各待求量的值。 以下就按上述四个步骤进行解题。 (1)系统的等值电路：等值电路如图3-6(b)所示（未计负荷）。其中，阻抗均为标么值，功率基准 值为60MVA,电压基准值为平均额定电压。电抗值分别计算为 E39 ⑨o1 c2⑨⑨a3 8n 1288 3j015 j0.0751 @ 115kV ② T① 、j0 j01, (b) 图3-6例3-2图（一） (a)系统图；(b)等值电路 60 0-m=x0=0.183×1000.86=0.095