
An overview of Cog Xinyu Feng USTC
An overview of Coq Xinyu Feng USTC

What is Cog? A proof assistant developed by INRIA https://coq.inria.fr/ Coq is a formal proof management system.It provides a formal language to write mathematical definitions, executable algorithms and theorems together with an environment for semi-interactive development of machine-checked proofs
What is Coq? • A proof assistant developed by INRIA • https://coq.inria.fr/ • Coq is a formal proof management system. It provides a formal language to write mathematical definitions, executable algorithms and theorems together with an environment for semi-interactive development of machine-checked proofs …

What is Cog? A functional programming language with rich type sys. Define inductive data types and write algorithms manipulating them. All programs must terminate. A higher-order logic with interactive theorem prover Allows you to reason about mathematical structures and your programs Generates machine-checkable proofs A meta-language/logic Allows you to encode another language/logic and prove the properties of that language/logic
What is Coq? • A functional programming language with rich type sys. • Define inductive data types and write algorithms manipulating them. • All programs must terminate. • A higher-order logic with interactive theorem prover • Allows you to reason about mathematical structures and your programs • Generates machine-checkable proofs • A meta-language/logic • Allows you to encode another language/logic and prove the properties of that language/logic

Why Coq? To have more rigorous formal reasoning For mathematics and program verification Tools like Coq boost program verification
Why Coq? • To have more rigorous formal reasoning • For mathematics and program verification • Tools like Coq boost program verification

Program verification under attack Reports and Articles Social Processes and Proofs of Theorems and Programs [CACM1979] Richard A.De Millo Georgia Institute of Technology Richard J.Lipton and Alan J.Perlis Mathematical proofs can often Yale University be wrong! Program verification Mathematics is trustworthy because of the social process to would never work... check/validate proofs. But nobody would care or check proofs for programs:"The verification of even a puny program can run into dozens of pages,and there's not alight moment or a spark of wit on any of those pages.Nobody is going to run into a friend's office with a program verification...Nobody is ever going to read it
Program verification under attack Program verification would never work … Mathematical proofs can often be wrong! Mathematics is trustworthy because of the social process to check/validate proofs. But nobody would care or check proofs for programs: “The verification of even a puny program can run into dozens of pages, and there's not alight moment or a spark of wit on any of those pages. Nobody is going to run into a friend's office with a program verification … Nobody is ever going to read it.” [CACM 1979]

Problem addressed by tools like Coq Proofs are mechanized and machine-checkable through Curry-Howard isomorphism [first published paper in 1980] Proof checking is as simple as type checking ·Fully automatic Very simple algorithm No longer need to trust the proofs ·Check them! Only need to trust the proof checker Simple,can be reviewed by human experts
Problem addressed by tools like Coq • Proofs are mechanized and machine-checkable • through Curry-Howard isomorphism [first published paper in 1980] • Proof checking is as simple as type checking • Fully automatic • Very simple algorithm • No longer need to trust the proofs • Check them! • Only need to trust the proof checker • Simple, can be reviewed by human experts …
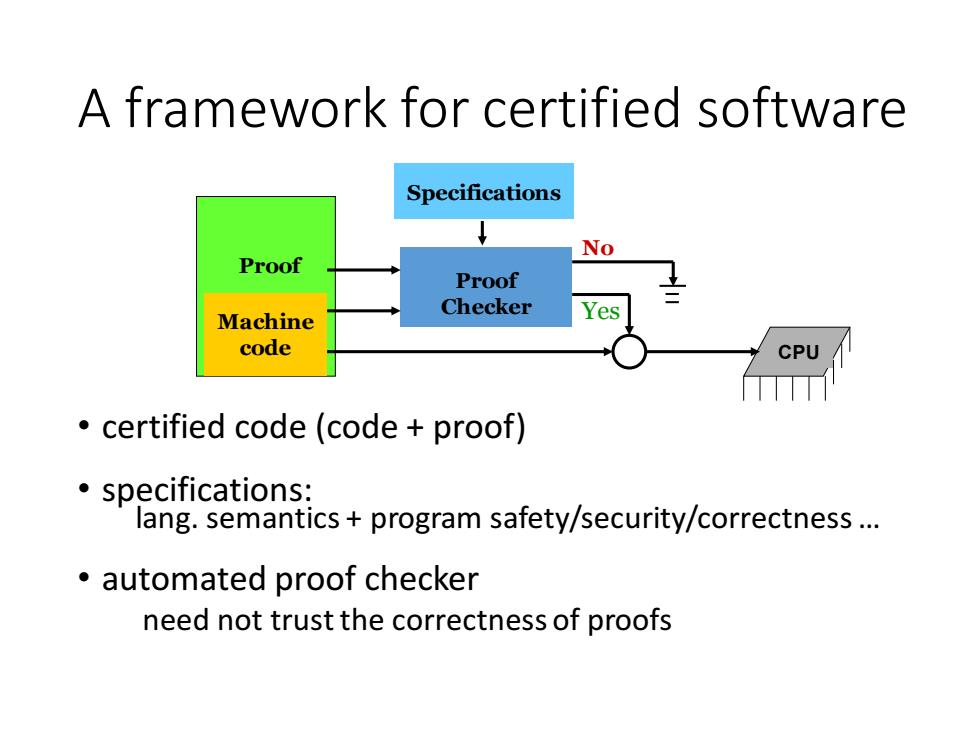
A framework for certified software Specifications ↓ No Proof Proof Checker Machine Yes code CPU certified code (code proof) ·specifications: lang.semantics+program safety/security/correctness... automated proof checker need not trust the correctness of proofs
A framework for certified software • certified code (code + proof) • specifications: lang. semantics + program safety/security/correctness … • automated proof checker need not trust the correctness of proofs Proof Checker Yes CPU Specifications Proof Machine code No

Applications of Coq Formal proofs of mathematical theorems Formal proof of 4-color theorem By Georges Gonthier and Benjamin Werner,2004 Other:Feit-Thompson theorem proved in Coq in 2012 ·Formal verification OS kernels and hypervisors CertiKOS project at Yale seL4 in Isabelle at NICTA ·Compilers CompCert at INRIA and following projects LLVM verification and Upenn 。Others Web servers (bedrock projects MIT) Certified software tool chains(e.g.,analysis algorithms)@Princeton 。Teaching:logic,programming languages,…
Applications of Coq • Formal proofs of mathematical theorems • Formal proof of 4-color theorem • By Georges Gonthier and Benjamin Werner, 2004 • Other: Feit–Thompson theorem proved in Coq in 2012 • Formal verification • OS kernels and hypervisors • CertiKOS project at Yale • seL4 in Isabelle at NICTA • Compilers • CompCert at INRIA and following projects • LLVM verification and Upenn • Others • Web servers (bedrock projects @ MIT) • Certified software tool chains (e.g., analysis algorithms) @ Princeton • Teaching: logic, programming languages, …

Gains lots of popularity AWARDS acm Software System Award MORE ACM AWARD WINNERS ABOUT THIS AWARD Awarded to an institution or individual(s)recognized for developing a software system that has had a lasting influence,reflected in contributions to concepts,in commercial acceptance,or both.The Software System Award carries a prize of $35,000.Financial support for the Software System Award is provided by IBM. Coq Selected As Recipient Of The 2013 Software System Award Other recipients of the award: Unix、TCP/IP、Norld-Wide Web、Java、Make、VMWare、 Eclipse、LLVM
Gains lots of popularity Other recipients of the award: Unix、TCP/IP、World-Wide Web、Java、Make、VMWare、 Eclipse、LLVM …

Demo: 。Small examples Imp in Coq (syntax and operational semantics)
Demo: • Small examples • Imp in Coq (syntax and operational semantics)