
Separation Logic (II) Acknowledgment:slides taken from Reynolds'mini-course CS 818A3
Separation Logic (II) Acknowledgment: slides taken from Reynolds’ mini-course CS 818A3

Specifications Partial correctness: ip}eta} Total correctness: [p]c[a] Note the spec now requires c does not abort
Specifications Partial correctness: Total correctness: Note the spec now requires c does not abort
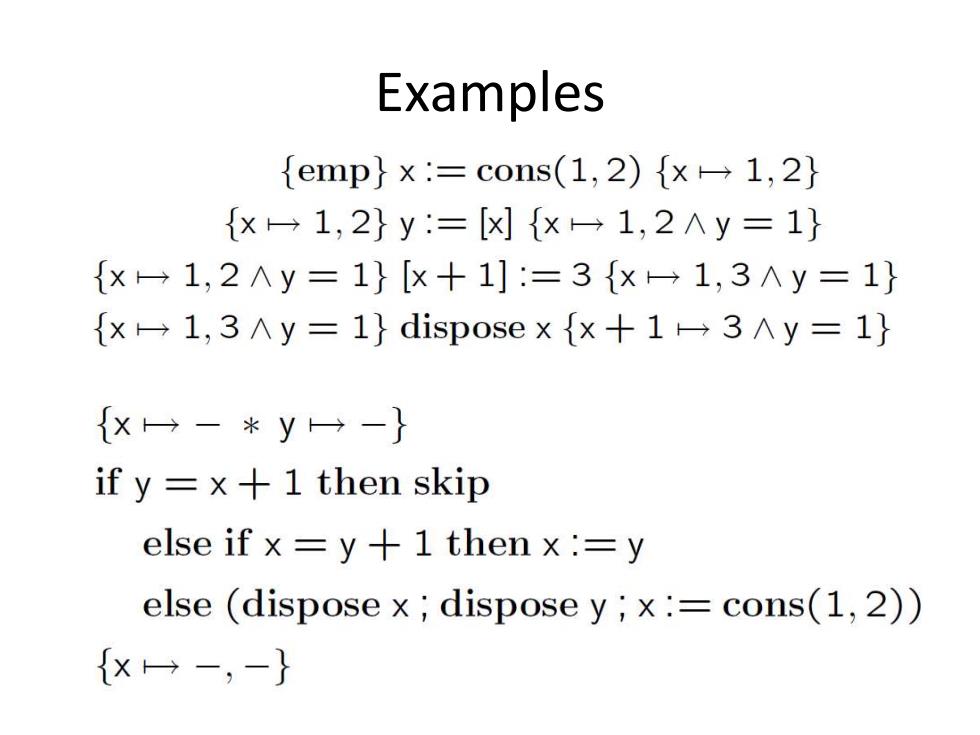
Examples {emp}×:=cons(1,2){x-1,2} {x一1,2}y=[]{x一1,2∧y=1} {x→1,2Λy=1}[x+1]:=3{x-1,3∧y=1} {x→1,3∧y=1}dispose×{×+1-3∧y=1} {X→-*y一-} if y =x+1 then skip else if x=y+1 then x:=y else (dispose x;dispose y;x:=cons(1,2)) {x一-,-}
Examples

The Frame Rule (O'Hearn)(FR) p}crar p r}ciq r}, where no variable occurring free in r is modified by c
The Frame Rule (O’Hearn) (FR)

Why the Frame Rule is Sound We define: If,starting in the state s,h,no execution of a com- mand c aborts,then c is safe at s,h. If,starting in the state s,h,every execution of c termi- nates without aborting,then c must terminate normally at s,h. Then our programming language satisfies: Safety Monotonicity If hh and c is safe at s,h-h, then c is safe at s,h.If h c h and c must terminate normally at s,h-h,then c must terminate normally at s,h
Why the Frame Rule is Sound

Why the Frame Rule is Sound The Frame Property If h Ch,cis safe at s,h-h,and some execution of c starting at s,h terminates normally in the state s',h', s,h-五.C—s,h2i c safe s',h' then hh'and some execution of c starting at s,h-h, terminates normally in the state s',h'-h
Why the Frame Rule is Sound
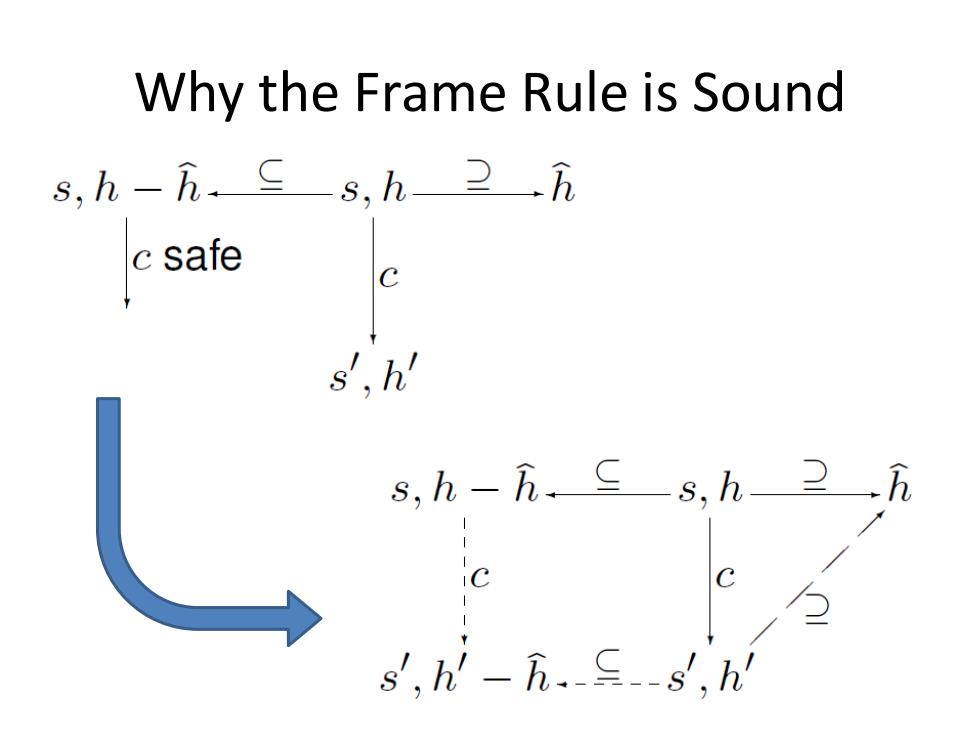
Why the Frame Rule is Sound s,h-i.c-s,h2一n csafe s,h' s,h-hi.s,h2.h C s,h-.-.-s/.h
Why the Frame Rule is Sound

Inference Rules for Mutation The local form(MUL): {e--}[e]:=e'{e-e}. The global form(MUG): {(e--)*r}[e]:=e'{(e-e)*r}. The backward-reasoning form(MUBR): {(e一-)*(e一e)-*p)}[e]:=e'{p}. One rule implies another
Inference Rules for Mutation One rule implies another

The local form(MUL): {e→-}[e]:=e'{e→ye The global form (MUG): {(e一-)*r}[e]=e'{(ee)*r}. One can derive(MUG)from(MUL)by using the frame rule: {(e→-)*r} {e→-} [e]:=e r {e-e) {(e→e)*r}

The local form (MUL): {e→-}[e]:=e'{e→e'} The global form(MUG): {(e--)*r}[e]:=e'{(e-e)*r}. To go in the opposite direction it is only necessary to take r to be emp: {e→-} {(e--)*emp} [e]:=e {(e一e)*emp} {e-e'}